Tabla de contenido
introducción
El teorema de superposición se utiliza mucho al analizar circuitos eléctricos lineales que constan de dos o más fuentes independientes (voltaje o corriente, o ambas), especialmente en el dominio del tiempo con elementos que operan a diferentes frecuencias (para circuitos). Si un circuito de CC lineal tiene múltiples fuentes independientes, puede utilizar técnicas de análisis nodal o de malla para encontrar la corriente (a través de la resistencia) y el voltaje (a través de la resistencia).
[adsense1]
Alternativamente, puede utilizar el teorema de superposición, que suma los efectos de las fuentes individuales a los valores de las variables que se están determinando. Esto se debe a que el teorema de superposición considera cada fuente en un circuito particular por separado para encontrar el valor de una variable (corriente o voltaje) y finalmente suma todas las variables causadas por cada efecto de fuente para generar una variable. Aunque el procedimiento es complejo, se puede aplicar a cualquier circuito lineal.
Volver a la cima
Descripción del teorema de superposición
El teorema de superposición establece que en una red lineal bidireccional que consta de dos o más fuentes de alimentación independientes, la corriente que fluye a través de un elemento (o el voltaje a través de él) causada por cada fuente de alimentación independiente que funciona sola es. Afirma que es la suma algebraica de las corrientes (voltajes a través) que fluyen a través de los elementos. Todas las demás fuentes son reemplazadas por resistencias internas. Sabemos que mientras exista linealidad entre las fuentes y las contribuciones, la suma de las contribuciones de diferentes fuentes que operan simultáneamente es igual a la suma algebraica de las contribuciones individuales de cada fuente que operan al mismo tiempo.
Por lo tanto, si un circuito consta de N fuentes independientes, entonces es necesario analizar N circuitos y cada uno de ellos produzca resultados para las fuentes individuales. Y finalmente, necesitamos sumar estos resultados individuales para realizar un análisis de todo el circuito. Por tanto, aunque esto requiere más trabajo, este teorema es muy útil a la hora de analizar diferentes partes de circuitos complejos.
Volver a la cima
Pasos para analizar el teorema de superposición
1. Considere diferentes fuentes de alimentación independientes dentro de un circuito determinado.
2. Seleccione y conserve una de las fuentes independientes y reemplace todas las demás fuentes con resistencias internas o reemplace las fuentes de corriente con circuitos abiertos y las fuentes de voltaje con cortocircuitos.
3. Vuelva a etiquetar las designaciones de voltaje y corriente de manera adecuada para evitar confusiones.
4. Utilice varias técnicas de reducción de circuitos para encontrar el voltaje/corriente requerido para que una fuente de alimentación funcione por sí sola.
5. Repita los pasos 2 a 4 para cada fuente independiente en el circuito dado.
6. Sume algebraicamente todos los voltajes/corrientes disponibles de cada fuente individual (considerando el signo del voltaje y la dirección de la corriente mientras suma).
[adsense2]
Volver a la cima
ejemplo :
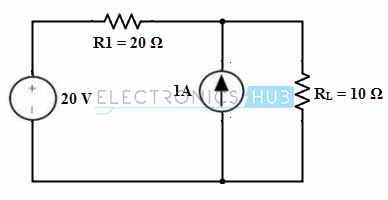
1. Para aplicar el teorema de superposición y obtener el voltaje a través de una resistencia de 10 ohmios (terminales de carga), considere el circuito de CC simple a continuación. Considere que un circuito dado tiene dos fuentes de alimentación independientes como fuentes de voltaje y corriente, como se muestra en la figura.
2. Primero, mantenga una fuente a la vez. Esto significa que solo la fuente de voltaje está activa en el circuito y la fuente de corriente se reemplaza por una resistencia interna (que es infinita), lo que resulta en un circuito abierto como se muestra en el diagrama.
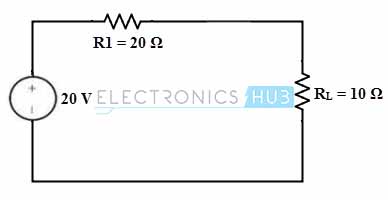
Por favor considere V.L1 es el voltaje a través de los terminales de carga cuando la fuente de voltaje funciona de forma independiente.
VL1 = Vs × Rl /(Rl +R1)
= 20 × 10 / (10 + 20)
= 6,66 voltios
3. Conserve solo la fuente de corriente y reemplace la fuente de voltaje con su resistencia interna (cero) y cortocircuito como se muestra.
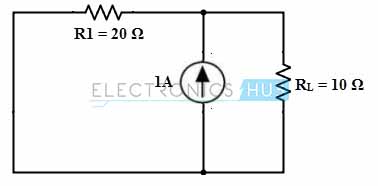
Consideremos V.L2 Este es el voltaje entre los terminales de carga cuando la fuente de corriente funciona de forma independiente.después
VL2 = yol ×Rl
Il = Yo × R1 /(R1 +Rl)
= 1 × 20 / (20 +30)
= 0,4 amperios
VL2 = 0,4 × 10
= 4 voltios
Por lo tanto, según el teorema de superposición, el voltaje a través de la carga es la suma de V.L1 y VL2
Vl =vL1 +VL2
= 6,66 + 4
= 10,66 voltios
Ejemplo 2:
Considere el siguiente circuito que utiliza el teorema de superposición para encontrar la corriente I a través de una resistencia de 4 ohmios.
Considere que I1, I2 e I3 son las corrientes de los suministros de 12 V, 20 V y 4 A, respectivamente. Y basado en el teorema de superposición I = I1 + I2 + I3. Ahora determinemos estas corrientes para cada fuente individual.
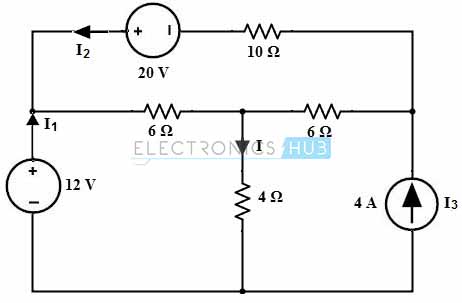
Volver a la cima
Fuente de voltaje de 12 V únicamente:
Considere el circuito a continuación donde solo se mantiene la fuente de alimentación de 12 V en el circuito y las otras fuentes de alimentación se reemplazan por resistencias internas.
Combinando una resistencia de 6 ohmios y una resistencia de 10 ohmios se obtiene una resistencia de 16 ohmios en paralelo con una resistencia de 6 ohmios. Esta combinación produce 16 × 6 / (16 + 6) = 4,36 ohmios. Por tanto, el circuito equivalente es el que se muestra en la figura.
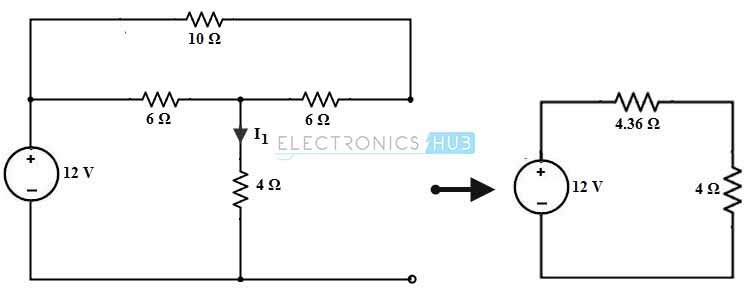
Entonces la corriente que fluye a través de la resistencia de 4 ohmios,
I1 = 12/8,36
= 1,43A
Solo fuente de voltaje de 20 V:
Si mantenemos solo la fuente de voltaje de 20 V y reemplazamos las otras fuentes de voltaje con resistencias internas, el circuito se ve así:
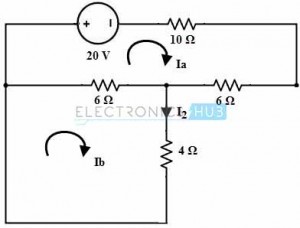
La aplicación del análisis de malla para realizar un bucle produce:
22Ia – 6Ib +20=0
22Ia – 6Ib = -20 …………….(1)
Para el bucle b:
10yob – 6Ia = 0
Ia = 10Ib/6
Sustituye Ib en la ecuación 1
22(10I)b/6) – 6Ib = -20
Ib = – 0,65
daraka, yo2 = Ib = -0,65
Solo fuente de corriente 4A
Considere el siguiente circuito, que retiene solo una fuente de corriente y reemplaza otras fuentes de corriente con resistencias internas.
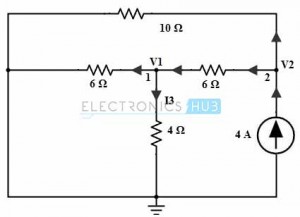
La aplicación del análisis de nodos en el nodo 2 produce:
4 = (V2/10) + (V2 –V1)/6 ……………..(2)
En el nodo 1,
(V1/6) + (V1/4) = (V2 –V1)/6
V2 = 3.496V1
Sustituyendo V2 en la Ecuación 2 se obtiene:
V1 = 0,766 voltios.
daraka, yo3 =v1/Cuatro
= 0,766/4
= 0,19 amperios.
Por tanto, según el teorema de superposición, I = I1 + yo2 + yo3
= 1,43 – 0,65 + 0,19
= 0,97 amperios.
Volver a la cima
Ejemplo de superposición usando un circuito de CA:
Considere el siguiente circuito de CA. Determine el valor de la corriente que fluye a través de la resistencia de 4 ohmios usando el teorema de superposición.
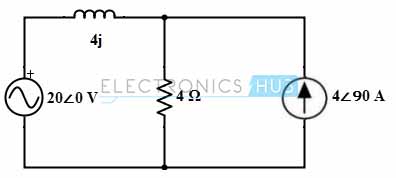
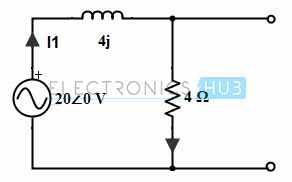
caso 1: Solo fuente de voltaje 20∠0
Manteniendo solo la fuente de voltaje en el circuito, la corriente que fluye a través del circuito se determina como:
I1 = 20∠0/(4 + j4)
= 20∠0 / (5,65∠45)
= 3,53∠- 45 o 2,49 –j2,49 A
Caso 2: 4∠90 fuente de corriente solamente
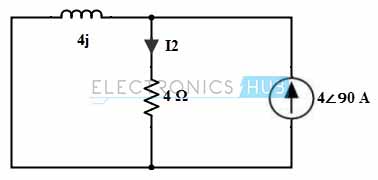
Manteniendo solo la fuente de corriente en el circuito, la corriente I2 que fluye a través del circuito se puede encontrar como:
Por el método de división actual, I2 = 4∠90 × 4j/(4 + j4)
= 4∠90 × 4∠90 (5,65∠45)
= 4∠90 × 0,707∠45
= 2,828∠135 o -1,99 + j1,99A
La corriente resultante que fluye a través de la resistencia de 4 ohmios es I = I1 + I2.
= 3,53∠-45 + 2,828∠135
= 0,785∠45 o 0,56 + j0,56 A
Volver a la cima
Límites del teorema de superposición
1. Al calcular potencias, el teorema de superposición no se puede utilizar porque funciona según la linealidad. La ecuación de potencia no es lineal porque es el producto del voltaje y la corriente, o la corriente al cuadrado, o el voltaje al cuadrado. Por tanto, el teorema de superposición no puede calcular la potencia disipada por los elementos en un circuito particular.
2. Si la selección de carga es variable o la resistencia de la carga cambia con frecuencia, todas las contribuciones de la fuente de corriente o voltaje y su suma deben realizarse para cada cambio en la resistencia de la carga. Por tanto, se convierte en un procedimiento muy complejo para analizar circuitos complejos.
3. Este teorema es aplicable sólo a circuitos lineales y no a circuitos no lineales (incluidos transistores y diodos).
4. Este teorema se aplica sólo cuando hay múltiples fuentes en el circuito.
Volver a la cima