Tabla de contenido
- Introducción al Teorema de Superposición
- Definición y Principios Básicos
- Cuándo y Por Qué Usar el Teorema de Superposición
- Cómo Aplicar el Teorema de Superposición
- Procedimiento Paso a Paso
- Ejemplo Práctico: Resolución de un Circuito
- Experimentación y Aplicaciones
- Aplicaciones del teorema de superposición
- Conclusión: Comprendiendo el Teorema de Superposición
- Puntos Clave:
Introducción al Teorema de Superposición
Definición y Principios Básicos
Descubre cómo el teorema de superposición se utiliza en ingeniería eléctrica para resolver redes complejas. Aprende a determinar voltajes y corrientes entre elementos, calculando el efecto de cada fuente de energía por separado.
El teorema de superposición establece:
“En una red bidireccional lineal con más fuentes, la respuesta (voltaje y corriente) de cualquier elemento es igual a la suma de todas las respuestas causadas por las fuentes individuales que actúan solas. Otras fuentes se eliminan del circuito”.
En otras palabras, considere solo una fuente independiente actuando a la vez. Por lo tanto, otras fuentes deben eliminarse. Una fuente de voltaje está en cortocircuito y una fuente de corriente está abierta para una fuente ideal. Dada la resistencia interna de la fuente, se debe considerar el circuito.
El teorema de superposición se aplica solo a circuitos que obedecen la ley de Ohm.
Cuándo y Por Qué Usar el Teorema de Superposición
¿Cuándo y por qué usar el teorema de superposición en tus proyectos? Para aplicarlo, la red debe cumplir ciertos requisitos:
- Los componentes utilizados en los circuitos deben ser lineales. Es decir, para una resistencia, el flujo de corriente es proporcional al voltaje. Para los inductores, el enlace de flujo es proporcional a la corriente. Por lo tanto, las resistencias, los inductores y los capacitores son elementos lineales. Pero los diodos y los transistores no son elementos lineales.
- Los componentes del circuito deben ser elementos bidireccionales. Es decir, la magnitud de la corriente es independiente de la polaridad de la fuente de energía.
- Con la ayuda del teorema de superposición, podemos encontrar la corriente a través del elemento, la caída de tensión en la resistencia y la tensión de nodo. Pero no puedo encontrar el poder disipado del elemento.
Cómo Aplicar el Teorema de Superposición
Paso 1: Identifica todas las fuentes independientes disponibles en la red. Aprende cómo el teorema de superposición puede simplificar el análisis de circuitos complejos
Paso 2: Seleccione cualquier fuente y elimine todas las demás fuentes. Si la red consta de fuentes dependientes, no se puede eliminar. Queda en el cálculo.
Si consideramos que todas las fuentes de energía son fuentes de energía ideales, no necesitamos considerar la resistencia interna. También corta directamente la fuente de voltaje y la fuente de corriente abierta. Sin embargo, dada la resistencia interna de la fuente de alimentación, se debe reemplazar la resistencia interna.
Paso 3: Ahora, solo hay una fuente de energía independiente en el circuito. Necesitamos encontrar una respuesta con una sola fuente de energía en el circuito.
Paso 4: Repita los pasos 2 y 3 para todas las fuentes de energía disponibles en su red. Si tiene 3 fuentes independientes, deberá repetir estos pasos 3 veces. Y cada vez que obtengo el valor de la respuesta.
Paso 5: Ahora combine todas las respuestas por suma algebraica obtenida de fuentes individuales. Y obtenga el valor final de la respuesta para un elemento particular de la red. Si necesita encontrar respuestas para otros elementos, deberá repetir estos pasos para ese elemento.
Procedimiento Paso a Paso
Ejemplo Práctico: Resolución de un Circuito
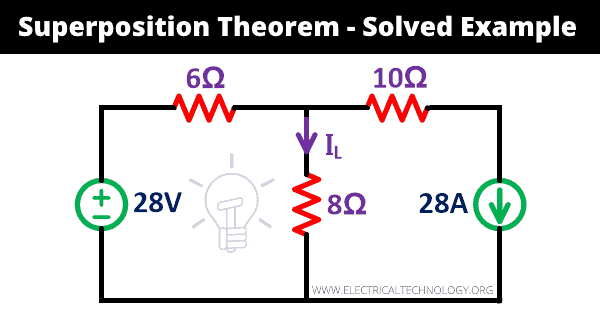
Ejemplo:
Entendamos cómo funciona el teorema de superposición con un ejemplo. actual (yol) pasa a través de las resistencias de 8 Ω en la red especificada utilizando el teorema de superposición.
Resolución:
Paso 1 Dada una fuente de voltaje y una fuente de corriente como se muestra en la red de arriba. Por lo tanto, debe repetir este paso dos veces.
Paso 2 Primero, considere la presencia de una fuente de voltaje de 28V en la red. Por lo tanto, la fuente de corriente debe eliminarse abriendo el terminal. Por lo tanto, consideramos la fuente de corriente como una fuente de corriente ideal. Por lo tanto, no hay necesidad de conectar una resistencia interna.
El resto del circuito se muestra a continuación.
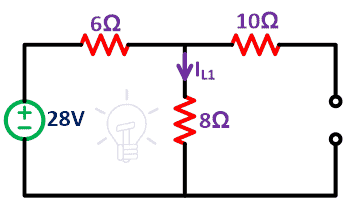
Paso 3 actual (yoL1) pasa a través de una resistencia de 8Ω. Solo obtienes el efecto de la fuente de voltaje.
Debido al circuito abierto de la fuente de corriente, no pasará corriente a través de la resistencia de 10 Ω. Por lo tanto, la red consta de un solo bucle.
Aplique KVL al bucle.
28 = 6Il1 +8Il1
28 = 14Il1
Il1 = 28/14
Il1 = 2A
Paso 4 Luego repita los mismos pasos para la fuente actual. En este estado, cortocircuite y elimine la fuente de voltaje. El resto del circuito se muestra a continuación.
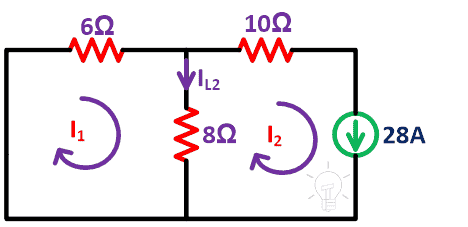
Hay dos bucles a considerar aquí.I1 y yo2 es la corriente de bucle.y encuéntrame ahoraL2.
Aplique KVL al bucle 1.
0 = 6I1 +8I1 – 8I2
14I1 – 8I2 = 0
La corriente a través del bucle 2 se calcula a partir de la fuente de corriente. Y así será.
I2 = 28A
Pon este valor en la fórmula anterior.
14I1 – 8 (28) = 0
I1 = 16A
donde la rama de resistencia de 8 Ω es común a ambos bucles. Por lo tanto, necesitamos encontrar la corriente resultante (IL2) pasa a través de una resistencia de 8Ω.
Il2 = I1 – I2
Il2 = 16 – 28
Il2 = -12A
Paso 5 Ahora combine los efectos de ambas fuentes por la suma algebraica de las corrientes. Por lo tanto, la corriente total a través de la resistencia de 8 Ω es IlLa dirección de la corriente es lo más importante aquí.yo ahoraL2 Tiene un signo menos. Esto significa que la corriente fluirá en direcciones opuestas mientras genera 28A. Y no puedes cambiar de dirección. Por eso estamos haciendo una suma algebraica mientras combinamos todas las fuentes.
Il = Il1 – Il2
Il = 2 + (-12)
Il = -10A
Aquí, suponga que la corriente que fluye a través de la resistencia de 8 Ω está en la dirección de la flecha en la figura. Un signo menos indica la dirección opuesta. Y la corriente es 8A.
Experimentación y Aplicaciones
Realiza un experimento práctico con el teorema de superposición siguiendo estos pasos. El objetivo es determinar la corriente a través de la resistencia y verificar cómo este teorema es aplicable en situaciones reales.
Objetivo
Determine la corriente a través de la resistencia y verifique el teorema de superposición.
Componentes necesarios
Fuentes de CC, resistencias, multímetros de CC, cables de conexión, protoboards, etc.
Hipótesis
El teorema de superposición se usa en el análisis de circuitos para encontrar las corrientes y voltajes entre elementos en un circuito dado. Este teorema es útil cuando el número de fuentes es grande.
Según el teorema de superposición, la respuesta del elemento es la suma algebraica de las respuestas de las fuentes de energía individuales.
Primero, calcule la corriente a través de las resistencias en una red dada. Si todas las fuentes están conectadas. Luego elimine las fuentes y encuentre la corriente de cada fuente individual. Finalmente, la suma de las corrientes medidas desde las fuentes individuales es similar a la medición de corriente cuando todas las fuentes están conectadas.
Procedimiento
Considere el circuito bidireccional lineal que se muestra en la siguiente figura.
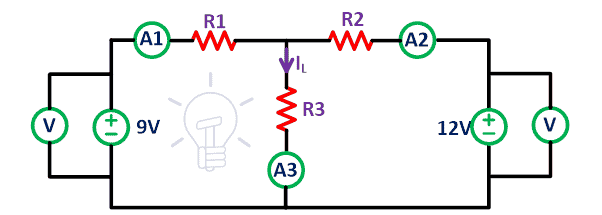
Conecte todos los elementos en la placa usando cables de conexión como se muestra en el circuito de arriba. Conecte un amperímetro a todas las resistencias para encontrar la corriente que pasa a través de ellas. Aquí tenemos dos fuentes de voltaje.
En el primer caso, medimos la corriente a través de todas las resistencias cuando ambas fuentes de voltaje están presentes en el circuito.Corriente que fluye a través de la resistencia R1R2y R3 dientes I1, I2y I3 Cada.
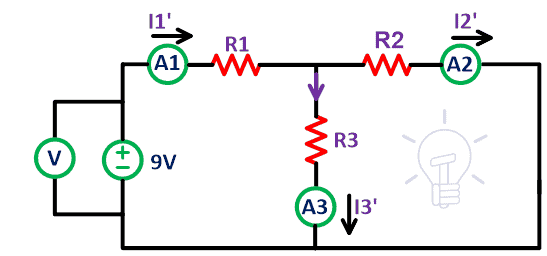
Ahora retire la fuente de voltaje de 12V del circuito. Cortocircuite los terminales A’ y B’ como se muestra arriba. Aquí asumimos que la fuente de voltaje es ideal. Por lo tanto, no hay necesidad de conectar una resistencia interna.ahora mide la corriente I1′, I2′ y I3′ Esta es la corriente a través de las resistencias R1, R2 y R3 respectivamente.
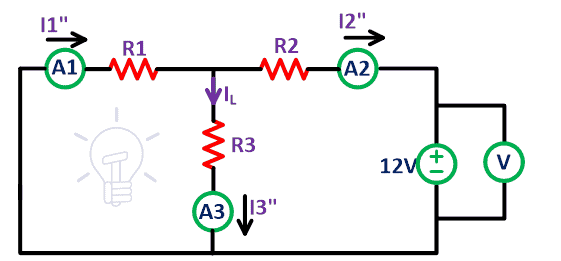
De manera similar, al quitar la fuente de voltaje de 9V, el circuito queda como se muestra arriba. Nuevamente, mida la corriente a través de todas las resistencias y nómbrelas I1“, I2“y I3“.
Ponga todos los valores en la tabla de observación a continuación.
Puesto de observación
| conexión de origen | r1 | r2 | r3 |
| ambas fuentes conectadas | I1 | I2 | I3 |
| Solo 12V está conectado | I1′ | I2′ | I3′ |
| Solo 9V está conectado | I1 pulgada | I2 pulgadas | I3 pulgadas |
Cálculo:
I1 = I1′ + I1 pulgada
I2 = I2′ + I2 pulgadas
I3 = I3′ + I3 pulgadas
Para verificar el teorema de superposición, compare la suma algebraica de las corrientes a través del resistor cuando las fuentes individuales están conectadas con la corriente medida cuando ambas fuentes están conectadas en el circuito.
Si se cumple el cálculo anterior, podemos probar el teorema de superposición.
Conclusión
En este experimento, podemos demostrar que la corriente a través de la resistencia es la suma algebraica de las corrientes cuando se conectan las fuentes de energía individuales. Luego probamos el teorema de superposición.
Aplicaciones del teorema de superposición
- El teorema de superposición se puede utilizar para redes de CA y CC.
- Cuantas más fuentes independientes tenga, más fácil será encontrar respuestas en la red.
- Calcular el efecto de cada fuente de energía por separado ayuda a calcular las rutas de corriente y los voltajes a través del elemento. Y después de poder determinar el efecto combinado sobre elementos de todas las fuentes.
Consideraciones y Limitaciones
- Es importante tener en cuenta las limitaciones del teorema de superposición. Por ejemplo, no se aplica a circuitos que solo tienen fuentes dependientes, y se requieren al menos dos fuentes independientes.
- Este teorema se aplica solo a redes que consisten en elementos lineales. No se puede aplicar a elementos no lineales como diodos y transistores.
- La potencia no se puede calcular con este teorema. La potencia no es lineal, por lo que es proporcional al cuadrado de la tensión y la corriente.
- Este teorema no es aplicable para condiciones en las que la resistencia varía con el voltaje y la corriente. El valor de la resistencia debe ser constante para todas las fuentes de energía.
- Este teorema se aplica solo a elementos bilaterales. Este teorema no se aplica si la respuesta de la red depende de la dirección de la corriente.
Conclusión: Comprendiendo el Teorema de Superposición
El teorema de superposición es una herramienta poderosa y versátil en el campo de la ingeniería eléctrica. A través de este análisis detallado, hemos explorado cómo este teorema permite descomponer circuitos complejos en componentes más manejables, facilitando el cálculo de voltajes y corrientes.
Puntos Clave:
- Definición y Aplicación: El teorema de superposición se aplica a circuitos lineales con múltiples fuentes independientes, permitiendo analizar el efecto de cada fuente por separado.
- Procedimiento y Ejemplos: Hemos presentado un procedimiento paso a paso, ilustrado con ejemplos prácticos, para aplicar este teorema en el análisis de circuitos.
- Experimentación y Aplicaciones Reales: La sección de experimentación mostró cómo el teorema se puede verificar en un entorno práctico, destacando su relevancia en aplicaciones industriales y de investigación.
- Consideraciones y Limitaciones: Aunque poderoso, el teorema tiene sus limitaciones y no se aplica en todos los contextos, como en circuitos con solo fuentes dependientes.