En este tutorial, aprenderemos sobre el teorema de Norton. El teorema de Norton, junto con el teorema de Thevenin, forma un concepto importante en el campo del análisis de circuitos eléctricos.
Tabla de contenido
- introducción
- enunciado del teorema de norton
- Pasos para analizar el teorema de Norton
- Ejemplo de cómo encontrar el circuito equivalente de un circuito de CC.
- Relación entre el teorema de Norton y el teorema de Tebinin
- Ejemplo de encontrar el circuito equivalente de un circuito de CA.
- Artículo relacionado:
introducción
A diferencia del teorema de Thevenin, el teorema de Norton reemplaza parte del circuito por un circuito equivalente que consta de una fuente de corriente y una resistencia en paralelo. Este teorema es una extensión del teorema de Thevenin, propuesto por EL Norton en 1926.
De manera similar al teorema de Thevenin, también se utiliza para calcular variables de carga como voltaje de carga, corriente de carga y potencia de carga con cálculos simples en comparación con otras técnicas de reducción de circuitos. Por lo tanto, este teorema también se llama dual del teorema de Thevenin. En la mayoría de los casos, la elección de la resistencia de carga para transferir la máxima potencia a la carga está determinada por el teorema de Thevenin o Norton.
Volver a la cima
enunciado del teorema de norton
El teorema de Norton establece que cualquier red lineal de dos terminales que consta de fuentes independientes y resistencias lineales puede reemplazarse por un circuito equivalente que consta de una fuente de corriente y una resistencia en paralelo.
La magnitud de esta fuente de corriente equivalente es igual a la corriente de cortocircuito que fluye a través de los terminales de carga, y la resistencia equivalente es la resistencia de los terminales de carga cuando todas las fuentes de corriente en un circuito determinado se reemplazan por resistencias internas.
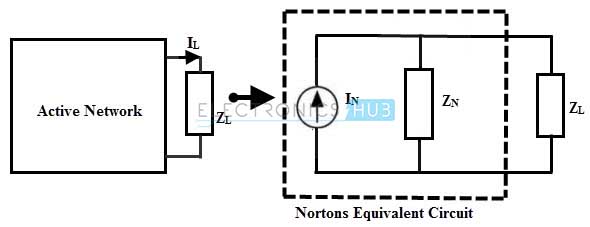
En el siguiente diagrama, parte de la red que consta de una fuente de alimentación (voltaje o corriente, o ambas) y una resistencia se reemplaza por una fuente de corriente y una resistencia en paralelo para que la corriente que fluye a través de la carga sea la misma en ambos casos. Soy.
Para un circuito de CA, esto se puede expresar como: Una red activa de dos terminales que consta de fuentes de alimentación e impedancias independientes se puede reemplazar por un circuito equivalente que consta de fuentes de corriente constante con impedancias paralelas.
El valor de la fuente actual es igual a la corriente que fluye a través de los terminales en cortocircuito de la red. Además, la impedancia paralela es la impedancia equivalente vista desde el terminal en cortocircuito cuando todas las fuentes de energía se reemplazan con impedancias internas.
Volver a la cima
Pasos para analizar el teorema de Norton
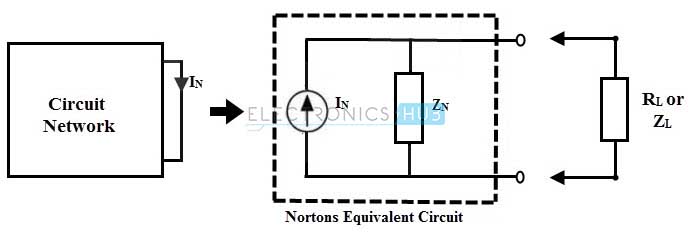
Para encontrar la variable de carga usando el teorema de Norton, necesitamos determinar los parámetros equivalentes de Norton. Son la magnitud de la corriente Norton o fuente de corriente equivalente y la resistencia Norton Rn o impedancia ZN. Para determinarlos se requieren los siguientes pasos:
1. Teniendo en cuenta el circuito dado, elimine la resistencia de carga (impedancia en el caso de un circuito de CA) del terminal de salida o del terminal de carga, luego cortocircuite el terminal de carga.
2. Aplicar técnicas de reducción de circuitos como análisis de malla, análisis de nodos y teorema de superposición para determinar la corriente de cortocircuito IN que fluye a través del terminal de cortocircuito. O simplemente mida experimentalmente la corriente de carga con un amperímetro.
3. Vuelva a dibujar el circuito dado reemplazando todas las fuentes de alimentación reales en el circuito con voltajes internos o simplemente cortocircuitando las fuentes de voltaje y abriendo las fuentes de corriente. Además, asegúrese de abrir o quitar los terminales de cortocircuito de la carga.
4. Calcule la resistencia (o impedancia) que existe entre los terminales de carga cuando se ve desde los terminales de carga. Esta resistencia es equivalente a la resistencia Norton RN o (impedancia ZN).
5. Inserte una resistencia (o impedancia) en paralelo con la fuente de corriente IN para formar el circuito equivalente de Norton.
6. A continuación, vuelva a conectar la carga al circuito equivalente de Norton y calcule la corriente, el voltaje y la potencia asociados con la carga de la siguiente manera:
En un circuito de CC,
Corriente de carga, IL = IN × [RN / (RL + RN)]
Tensión de carga, VL = IL × RL
Pérdida de potencia en carga, P = IL2 × RL
En un circuito de CA,
Corriente de carga, IL = IN × [ZN / (ZL + ZN)]
Tensión de carga, VL = IL × ZL
Consumo de energía en carga, P = IL2 × ZL
Volver a la cima
Ejemplo de cómo encontrar el circuito equivalente de un circuito de CC.
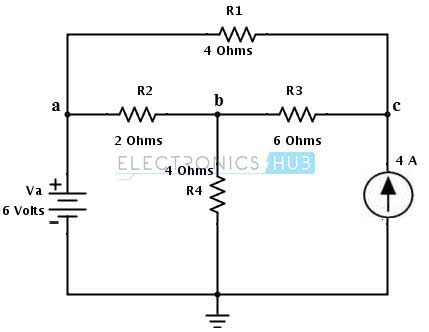
Considerando el mismo circuito de CC en el ejemplo del teorema de Thevenin, aplique el teorema de Norton para encontrar la corriente que fluye a través de una rama con una resistencia de carga de RL = R2 = 2 ohmios.
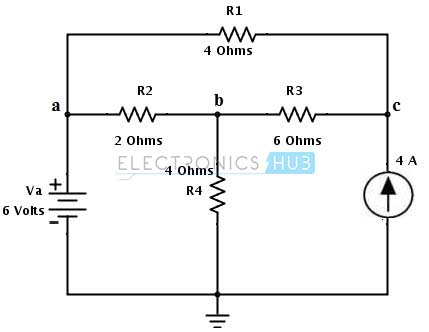
1. Retire la resistencia de carga y ponga en cortocircuito los terminales de carga a y b. Como se muestra en la figura, cada bucle representa la dirección del flujo de corriente.
2. Aplique un análisis de malla a cada bucle para encontrar la corriente IN que fluye a través del terminal en cortocircuito.
La aplicación de KVL al bucle 1 da como resultado:
6 – (I1 – I2) R4 = 0
Sustituir I2 = -4A
I1 = 6 – 16 / 4 = – 2,5A
La aplicación de KVL al bucle 3 da como resultado:
– I3R1 – (I3 – I2)R3 = 0
-4I3 – 6 (I3 + 4) = 0
– 10I3 = 24
I3 = – 2,4A
Por lo tanto, In = I1 – I3
= -2,5 + 2,4
= 0,1A, fluye de a a b.
3. El siguiente paso es determinar la resistencia equivalente RN. Para calcular esta resistencia, debes quitar los terminales en cortocircuito de la carga y reemplazar todas las fuentes con resistencias internas.
Entonces la resistencia total entre los terminales a y b, RN = 10 × 4 / 10 + 4
= 2,85 ohmios
4. Colocar la corriente In calculada anteriormente en paralelo con la resistencia Rn forma el circuito equivalente de Norton como se muestra en la figura. Para determinar la variable de carga, vuelva a conectar la resistencia de carga entre los terminales de carga.
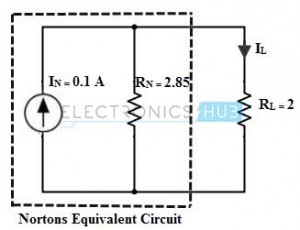
Entonces, la corriente de carga IL=IN×. [RN / (RL + RN)]
= 0,1 × [2.85/ (2 + 2.85)]
= 0,05 amperios
Usando los cálculos anteriores, el circuito original se verá similar a la figura siguiente que representa la corriente de carga en la rama ab.
Para diferentes valores de resistencia de carga, el flujo de corriente se determina como:
Cuando RL=8Ω
IL = 0,1 × [2.85 / (8 + 2.85)]
= 0,02A
Cuando RL=12Ω
IL = 0,1 × [2.85 / (12+ 2.85)]
= 0,01A.
Volver a la cima
Relación entre el teorema de Norton y el teorema de Tebinin
Comparando el ejemplo anterior con el ejemplo del problema de Thevenin, vemos que el circuito equivalente de Norton de la red lineal constituye una fuente de corriente Norton IN en paralelo con la resistencia de Thevenin Rth.
Por tanto, es posible realizar una transformación de fuente del circuito equivalente de Thevenin para obtener el circuito equivalente de Norton, y viceversa.
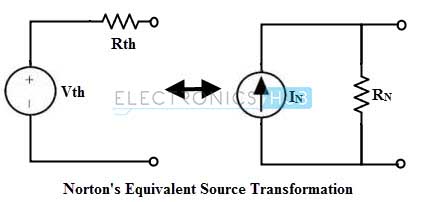
A partir del circuito equivalente de Norton que utiliza conversión de potencia, la magnitud de la fuente de voltaje (Vth) y la resistencia en serie (Rth) se encuentran como:
Vth = RN × EN y
Rth = RN
En el ejemplo anterior
Vth = 2,85 × 0,1
= 0,28 voltios.
Por lo tanto, puedes analizar fácilmente tu circuito utilizando cualquiera de estos dos métodos. Sin embargo, los beneficios del teorema de Thevenin también se aplican al teorema de Norton. Estos métodos le permiten encontrar valores de corriente y voltaje para varios valores de resistencia de carga sin tener que realizar muchos cálculos complejos.
Por lo tanto, el teorema de Norton ayuda a que el diseño basado en aplicaciones sea mucho más fácil. El uso de estos dos teoremas está determinado por la aplicación que requiere estos equivalentes, como circuitos seguidores de corriente (usando equivalentes de Norton) o amplificadores de voltaje (usando equivalentes de Thevenin).
Volver a la cima
Ejemplo de encontrar el circuito equivalente de un circuito de CA.
Considere el siguiente circuito de CA que ya ha sido analizado utilizando el teorema de Thevenin. Este circuito utiliza el teorema de Norton para encontrar la corriente que fluye a través de una impedancia de 4+4j ohmios.
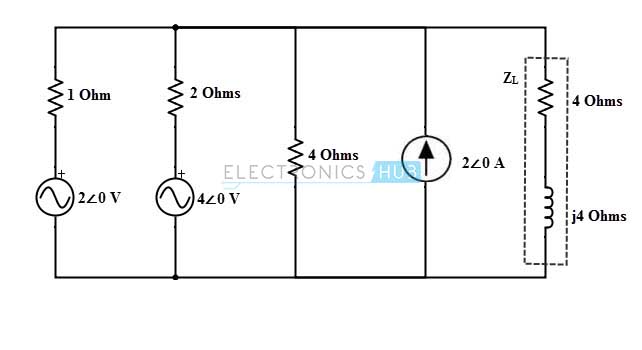
El circuito anterior consta de dos fuentes de voltaje que se pueden convertir en fuentes de corriente de la siguiente manera:
Is1 = Vs1/Rs1
= 2∠0/1
= 2A
similarmente
Is2 = Vs2/Rs2
= 4∠0/2
= 2A
Entonces el circuito se verá así.
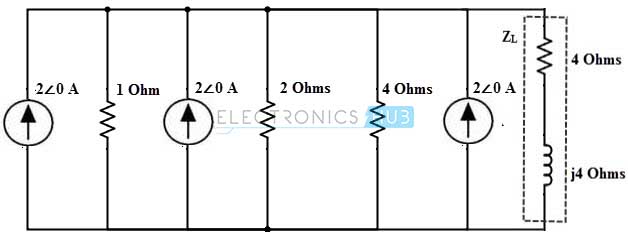
Para aplicar el teorema de Norton, desconecte la impedancia de carga y cortocircuite los terminales de carga como se muestra. Asuma la dirección de la corriente como se muestra en la figura.
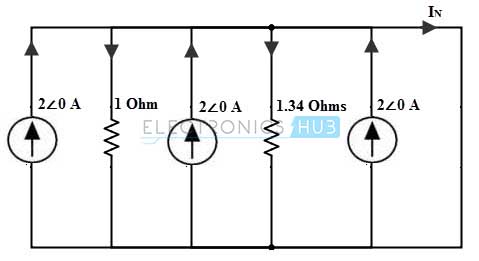
Considerando el diagrama anterior como un solo nodo, la corriente total es de 6 amperios y la combinación total de resistencias en paralelo es de 0,574 ohmios. Al convertir esto en una fuente de voltaje, la corriente Norton se puede encontrar como:
Vs = 6 ∠0 × 0,574
= 3,44∠0
Por lo tanto, IN = VN / 0,574
= 3,44∠0 / 0,574
= 5,97∠0A
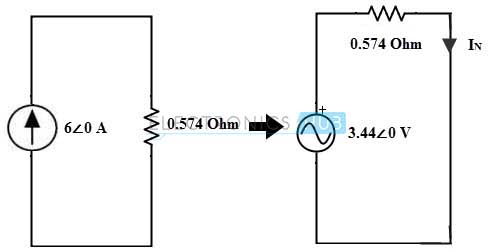
La impedancia equivalente de Norton es igual a la impedancia equivalente del circuito, ZN = 0,574.
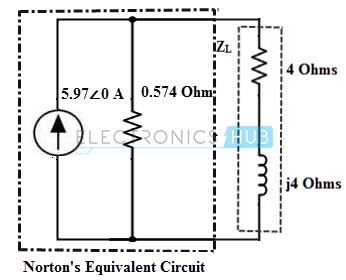
Por lo tanto, la corriente de carga a través de la impedancia 4 + j4 es IL = IN ×. [ZN / (ZL + ZN)]
= 5,97∠0× [0.574/ (4 + j4 + 0.574)]
= 3,42 / 6,07∠41,17
= 0,56 ∠-41,17 A
Este valor es el mismo que el obtenido en el ejemplo del circuito de corriente alterna de Thevenin. Por tanto, el teorema de Norton es el dual del teorema de Thevenin. Las limitaciones del teorema de Thevenin también se aplican al teorema de Norton.
Volver a la cima