Si ha leído un tutorial sobre la Ley de voltaje de Kirchhoff (KVL), ya sabe lo útil e importante que es KVL para el análisis de redes eléctricas. El conocimiento de KVL también es muy útil si estás estudiando materias como “Electrónica analógica” o “Sistemas de control”. Por lo tanto, el control adecuado de KVL es muy importante. En este tutorial, veremos un caso especial de KVL. ¿qué es eso? Vamos a revisar.
Antes de comenzar con los ejemplos, un breve resumen de KVL. Esto establece que las fuentes de voltaje y las caídas de voltaje en los elementos de la red en un circuito cerrado suman cero.
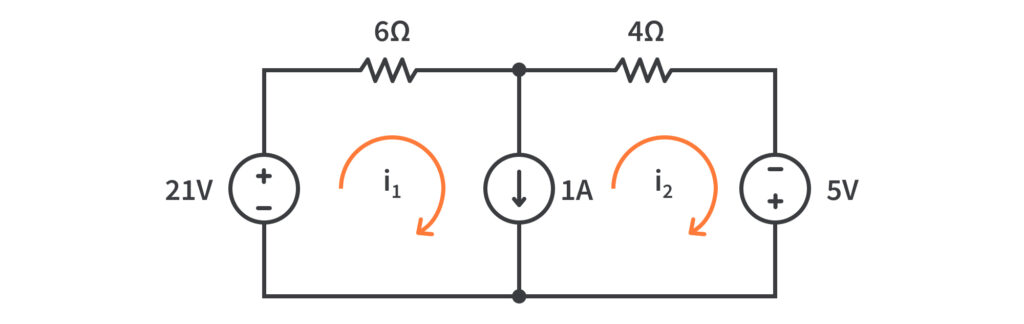
Considere la siguiente red.
Se supone que debemos encontrar la corriente de malla i.1 y yo2. Tómese un momento para recordar cómo se aplica KVL en el circuito cerrado de la red.
Empecemos comprobando el circuito. Podemos ver que hay dos resistencias y dos fuentes de voltaje, cuyos valores ya se proporcionan. La rama central también tiene una fuente de corriente que suministra 1A de corriente en dirección descendente. corriente de malla asignada i1 y yo2 Fluye en el sentido de las agujas del reloj. Es una buena idea recordar la dirección de la corriente de malla al resolver este tipo de problemas.
Podemos ver que la malla 1 tiene una fuente de voltaje de 21V, una resistencia de 6Ω y una fuente de corriente de 1A.
Por lo tanto, para cada KVL, la suma de las caídas de voltaje en la resistencia y la fuente de corriente debe ser igual a 21 voltios. Podemos calcular fácilmente la caída de voltaje a través de una resistencia usando la Ley de Ohm, pero ¿qué pasa con la fuente de corriente?¿Puedes ver el problema ahora?
No puedo encontrar la caída de voltaje en la fuente de corriente porque no conozco la resistencia de la fuente de corriente. Puede ser cualquier cosa. No tengo suficiente información en este momento para averiguarlo. Por lo tanto, se requiere una solución alternativa.
Primero, supongamos que la caída de voltaje de la fuente actual es un valor V.X.
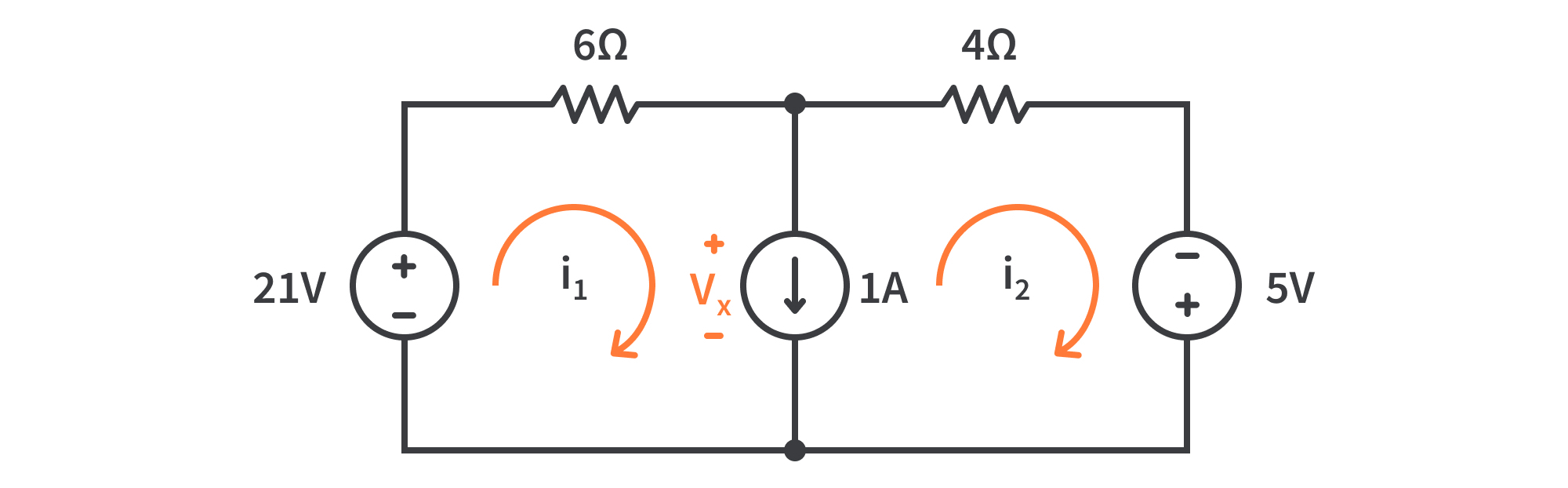
Ahora podemos aplicar KVL a la malla 1 considerando la caída de voltaje de la fuente de corriente como Vx y obtenemos esto:
Ordenar por VX obtenemos,
Del mismo modo, aplique KVL a la malla 2. Sin embargo, siempre verifique dos veces la polaridad de la fuente de voltaje antes de escribir la ecuación KVL.
Como habrás notado, ambas ecuaciones de malla tienen un término llamado Vx. Por lo tanto, podemos igualar las dos ecuaciones para obtener una ecuación de malla común.
Reorganizada, la ecuación de malla común es
aun tengo dos preguntas1 y yo2 Así que necesitamos otra ecuación para resolver esto. Aquí es donde la rama de origen actual es útil.
Como se puede ver en la figura, la corriente de malla i1 fluye en la misma dirección que la corriente 1A de la fuente de corriente,2 Opuesto a la dirección de la fuente de corriente. Se puede formar una relación matemática que describa este estado. Es:
Ahora tenemos dos ecuaciones para las dos incógnitas. Si no suspendes una clase de álgebra lineal, las matemáticas posteriores son bastante fáciles. La respuesta final se obtiene fácilmente resolviendo dos ecuaciones. Este es uno de los enfoques para resolver este problema. Sin embargo, me gustaría presentar otra forma relativamente corta de resolver este problema.conocido como “Super Malla” Método.
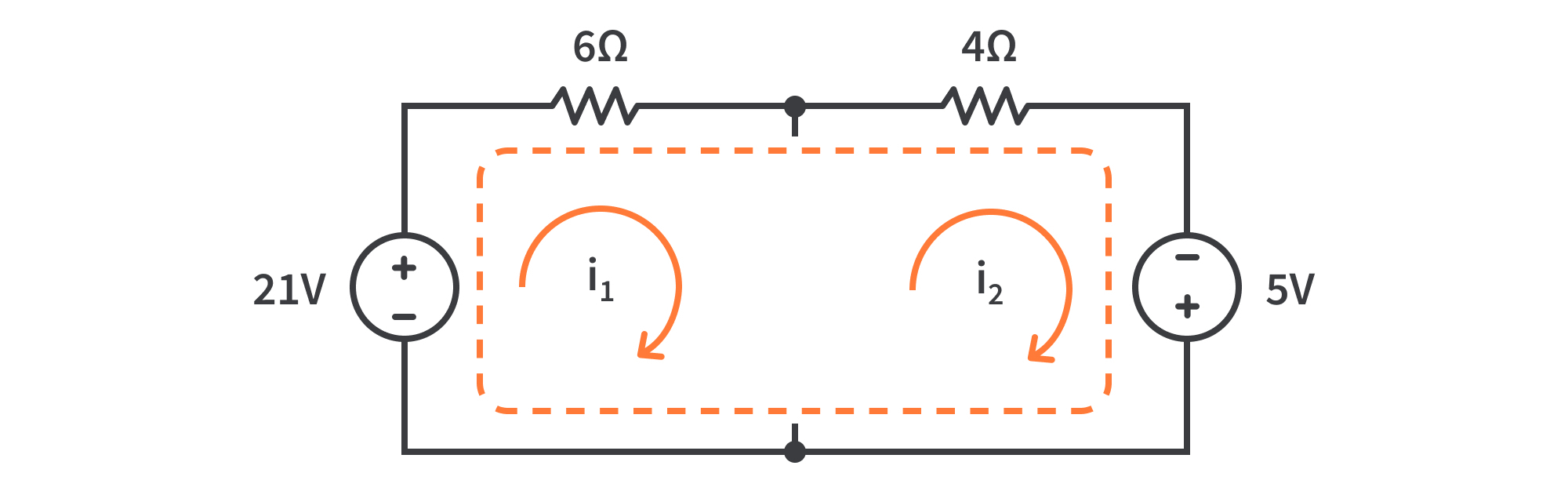
Rehagamos esta pregunta usando el método de “super malla”. No te preocupes, será mucho más rápido esta vez.
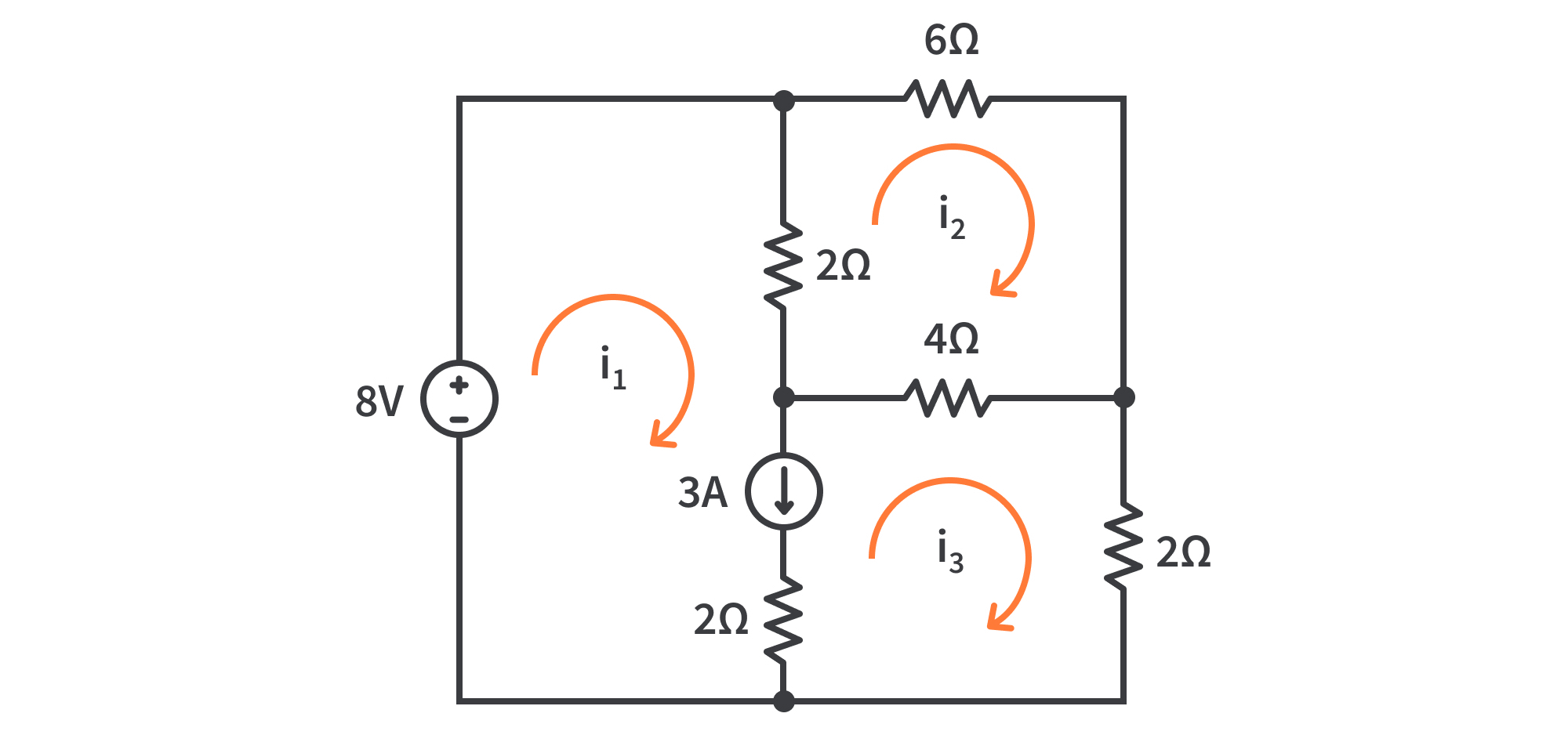
Esta vez nos dan una red con tres mallas. Además de las fuentes de resistencia y voltaje provistas dentro de la red, también hay una fuente de corriente compartida entre la malla 1 y la malla 3. Las fuentes actuales compartidas significan que es hora de usar el método “supermesh” nuevamente.
Elimine la rama que contiene la fuente actual para obtener una “súper malla” que consiste en la malla 1 y la malla 3.
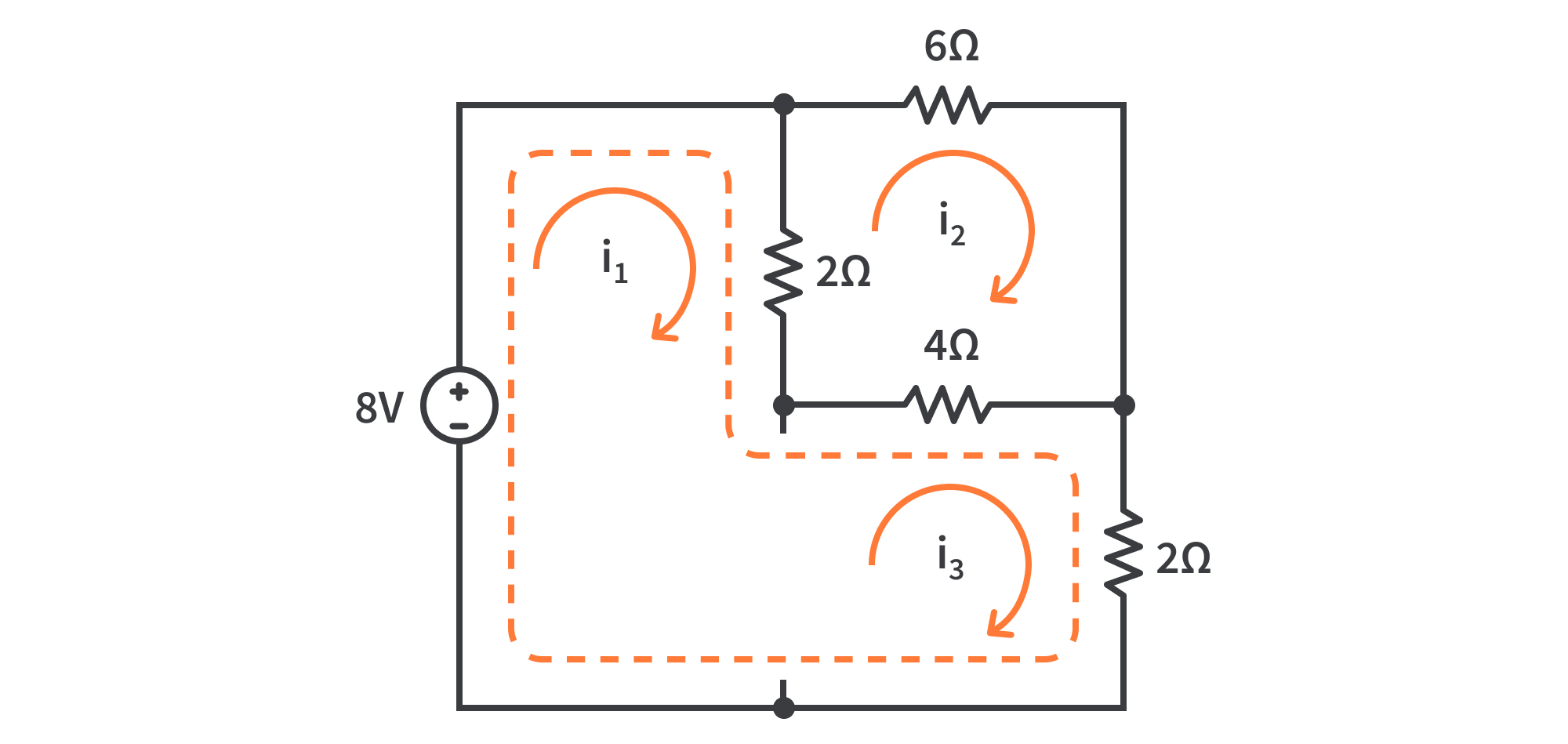
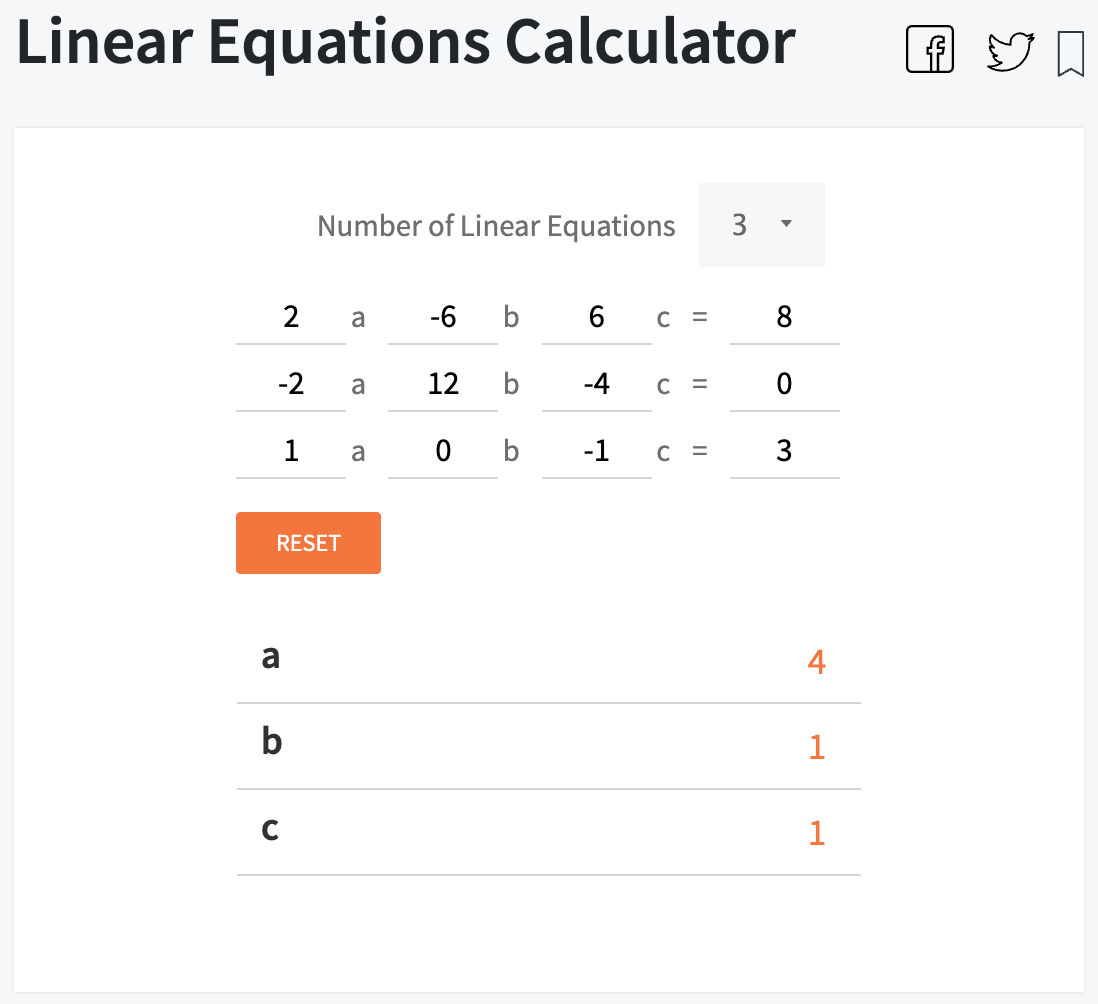
Finalmente, el valor de la corriente de malla se obtiene como
Ahora que tenemos las corrientes de malla, podemos hacer todo tipo de cosas, como mirar la corriente que fluye a través de cada elemento de la red. Luego puede usar la ley de Ohm para encontrar la caída de voltaje en la resistencia.
Esto agrega otra técnica a la caja de herramientas de análisis de red. Puede ver cuán conveniente y rápido puede ser el método de supermalla cuando se trata de redes tan complejas. Entonces, si tiene problemas con la fuente actual compartida entre dos mallas, use el método “supermesh” para facilitar un poco las cosas.