¿Qué es el teorema de transferencia de máxima potencia (MPTT)?

En este tutorial, aprenderá sobre el teorema de transferencia de potencia máxima (MPTT). Esta es una de las leyes fundamentales e importantes que define las condiciones necesarias para la máxima transferencia de potencia (que no debe confundirse con la máxima eficiencia).

introducción

En cualquier circuito eléctrico, la energía eléctrica de una fuente de energía se entrega a una carga, donde se convierte en trabajo útil. En realidad, toda la potencia entregada nunca está presente en la carga debido a los efectos del calentamiento y otras limitaciones de la red. Por lo tanto, existe una cierta diferencia entre fuerza de atracción y fuerza de transmisión.

El tamaño de la carga siempre afecta la cantidad de energía transferida desde la fuente. En otras palabras, a medida que cambia la resistencia de la carga, también cambia la potencia transferida a la carga. Por tanto, el teorema de transferencia de máxima potencia garantiza las condiciones ideales para transferir la máxima potencia a la carga. Echemos un vistazo al “cómo”.

Explicación del teorema de transferencia de máxima potencia.

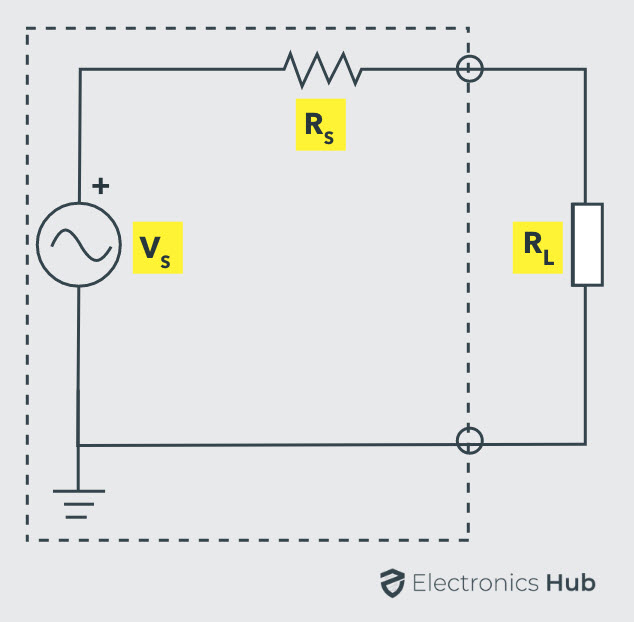
El teorema de transferencia de máxima potencia establece que en una red de CC bidireccional lineal, la potencia máxima se entrega a la carga cuando la resistencia de la carga es igual a la resistencia interna de la fuente.

En el caso de una fuente de voltaje independiente, su resistencia en serie (resistencia interna R_S) o, en el caso de una fuente de corriente independiente, su resistencia en paralelo (resistencia interna R_S) debe ser igual a la resistencia de carga R_l Proporciona máxima potencia a la carga.

Prueba del teorema de transferencia de máxima potencia.

El teorema de máxima transferencia de potencia garantiza el valor de la resistencia de carga que transfiere la máxima potencia a la carga.

Considere la siguiente red CC de dos terminales (circuito de la izquierda). La condición de potencia máxima se determina obteniendo una expresión para la potencia absorbida por la carga utilizando el método de corriente de malla o nodal y derivando la expresión resultante en términos de la resistencia de carga R._l.

Este es un procedimiento muy complicado. Sin embargo, en tutoriales anteriores hemos visto que partes complejas de la red pueden reemplazarse por sus equivalentes de Thevenin, como se muestra a continuación.

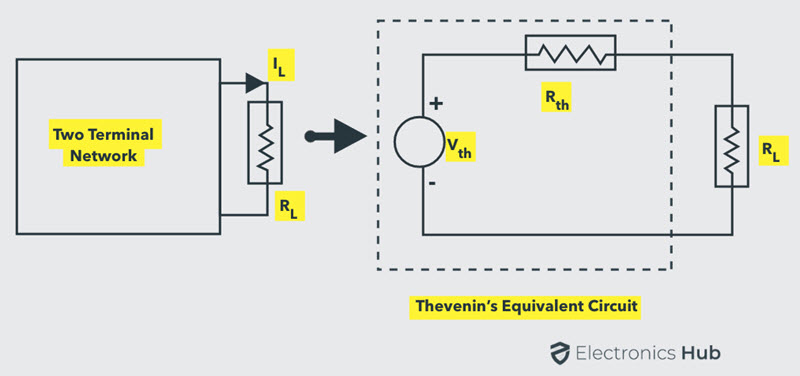
El circuito original de dos terminales se reemplaza por un circuito equivalente de Thevenin a través de una resistencia de carga variable. La corriente a través de la carga para cualquier valor de resistencia de carga es:

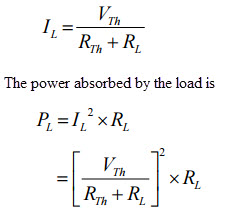
De la ecuación anterior, la potencia entregada depende del valor de R._T.H. y r_l. Sin embargo, dado que el equivalente de Thevenin es una constante, la potencia entregada a la carga desde esta fuente equivalente depende completamente de la resistencia de la carga R._l. Aplique una derivada a P para encontrar el valor exacto de RL._l Respecto a R_l Hazlo igual a cero como se muestra a continuación.

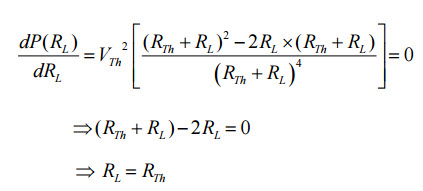
Por lo tanto, esta es la condición de adaptación de carga en la que se produce la máxima transferencia de potencia cuando la resistencia de la carga es igual a la resistencia de Thevenin del circuito. Al reemplazar R,_T.H. =R_l En la expresión anterior:

La potencia máxima entregada a la carga es

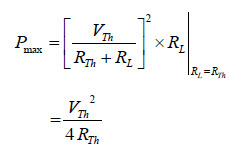
La potencia total transferida desde la fuente de alimentación es:

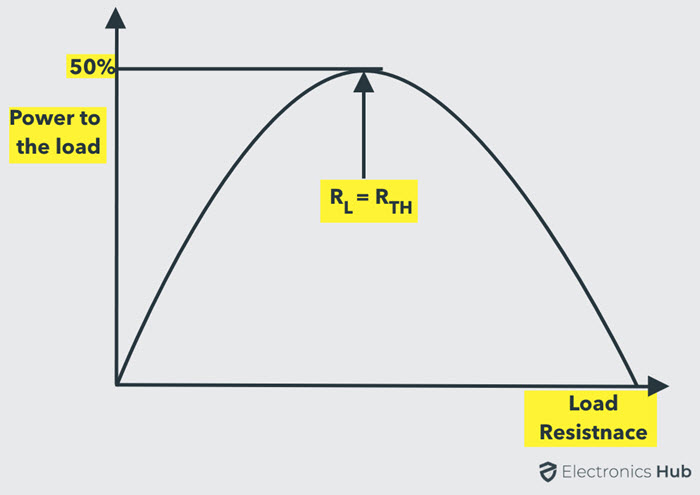
Por lo tanto, el teorema de transferencia de potencia máxima describe la condición en la que se entrega la potencia máxima a la carga, es decir, cuando la resistencia de la carga es igual a la resistencia equivalente de Thevenin del circuito. La siguiente figura muestra la curva de potencia entregada a la carga versus la resistencia de la carga.

Tenga en cuenta que si la resistencia de la carga es cero, la potencia entregada será cero ya que no hay caída de voltaje en la carga en esta condición. Además, la potencia es máxima cuando la resistencia de la carga es igual a la resistencia interna del circuito (o la resistencia equivalente de Thevenin). Nuevamente, no fluye corriente a través de la carga, por lo que cuando la resistencia de la carga llega al infinito, la potencia es cero.

Eficiencia de transferencia de energía

Debe recordarse que este teorema sólo indica la máxima transferencia de potencia, no la máxima eficiencia. Si la resistencia de la carga es menor que la resistencia de la fuente, la disipación de potencia en la carga se reduce y la mayor parte de la potencia se disipa en la fuente, lo que resulta en una menor eficiencia.

Considere la potencia total entregada a partir de la ecuación de potencia (Ecuación 2). La potencia se disipa en la resistencia de Thevenin equivalente R._T.H. Depende de la fuente de voltaje V_T.H..

Por tanto, la eficiencia en condiciones de máxima transferencia de potencia es:

Eficiencia = Salida / Entrada × 100

= yo_l² R_l / 2 yo_l² R_l ×100

= 50%

Por tanto, en condiciones de máxima transferencia de potencia, la eficiencia es del 50%. Esto significa que sólo la mitad de la potencia generada se entrega a la carga, como lo muestra la relación eficiencia-eficiencia, y en otras condiciones un pequeño porcentaje de la potencia se entrega a la carga. La transferencia de potencia máxima es la curva siguiente.

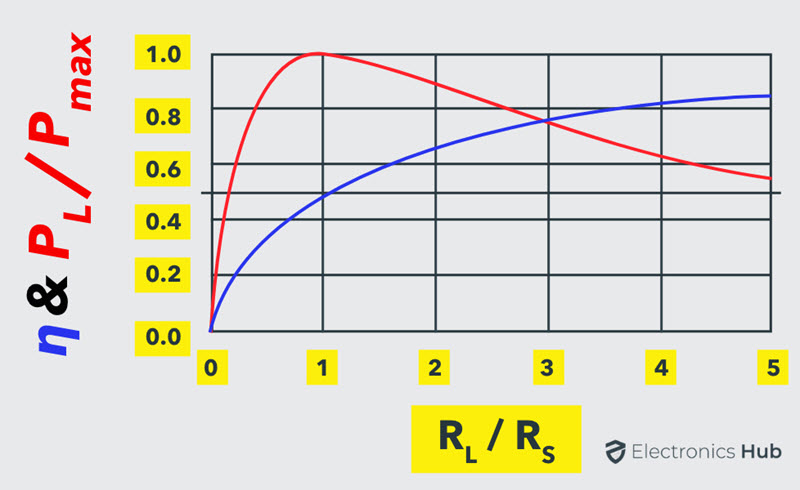
En algunas aplicaciones, como amplificadores o circuitos de comunicación, puede ser deseable transferir la máxima potencia a la carga en lugar de lograr una alta eficiencia.

Por otro lado, para sistemas de transmisión de energía con grandes resistencias de carga a través de la carga (mucho mayores que la resistencia de la fuente interna), es deseable lograr una mayor eficiencia que la transferencia de energía maximizada. Incluso si la eficiencia es alta, en tales casos se entregará menos energía.

Teorema de transferencia de potencia máxima para circuitos de CA

En una red activa, podemos decir que la potencia máxima se transfiere a la carga cuando la impedancia de la carga es igual al conjugado complejo de la impedancia equivalente de la red dada vista desde los terminales de carga.

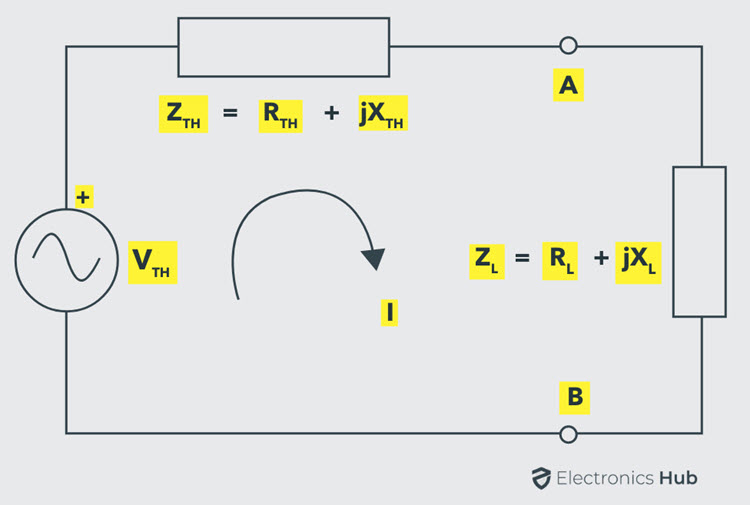
Considere el circuito equivalente de Thevenin anterior entre los terminales de carga, donde la corriente que fluye a través del circuito viene dada por:

potencia entregada a la carga,

Para obtener la máxima potencia, la derivada de la ecuación anterior debe ser cero. Simplificándolo, queda así:

Sustituyendo la relación anterior en la Ecuación 1 se obtiene:

Nuevamente, para una transferencia de potencia máxima, la derivación de la ecuación anterior debe ser igual a cero y puede simplificarse a:

Por lo tanto, para R, la potencia máxima se transfiere de la fuente a la carga._l =R_T.H. y X_l = –X_T.H. en un circuito de corriente alterna. Esto significa que la impedancia de carga debe ser igual al conjugado complejo de la impedancia equivalente del circuito.

ubicación Z_T.H. es el conjugado complejo de la impedancia equivalente del circuito.

Una vez transferida esta potencia máxima, PAG_máx. =v²_T.H. /4R_T.H. o V²_T.H./4R_l

Aplicación del ejemplo de transferencia de máxima potencia a un circuito de CC

Considere el siguiente circuito para encontrar el valor de la resistencia de carga que recibe la potencia máxima de la fuente de suministro y la potencia máxima en las condiciones de transmisión de potencia máxima.

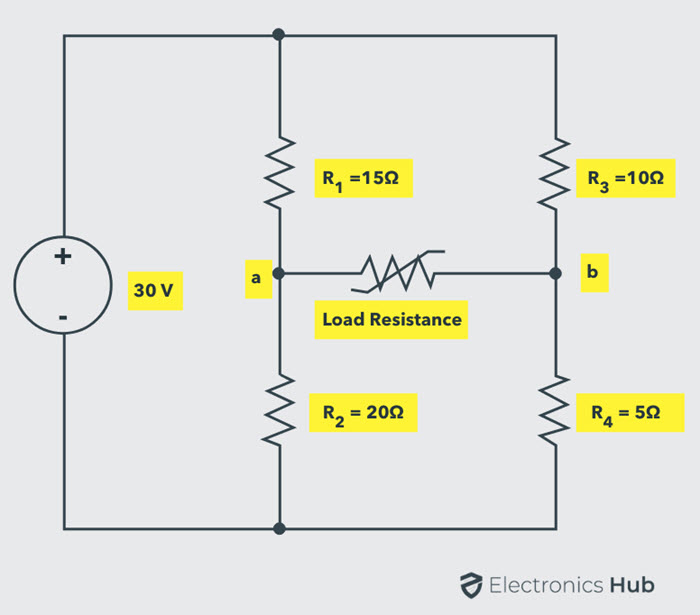
Retire la resistencia de carga de los terminales de carga a y b. Para representar el circuito dado como un circuito equivalente de Thevenin, necesitamos determinar el voltaje de Thevenin V._T.H. y la resistencia equivalente de Thevenin R_T.H..

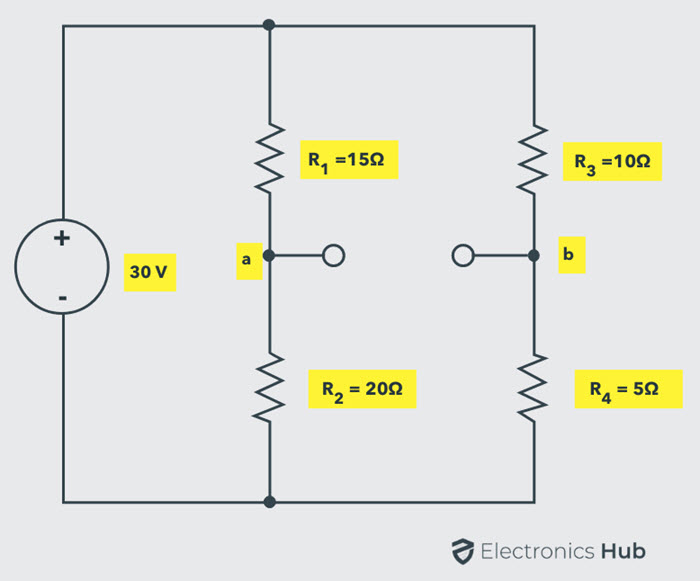
El voltaje de Thevenin o el voltaje entre los terminales ab es: V_abdominales =v_ser –V_b

V_ser = V × R2 / (R1 + R2)

= 30 × 20 / × (20 + 15)

= 17,14V

V_b = V × R4/(R3 + R4)

= 30 × 5 /(10 + 5)

= 10V

V_abdominales = 17,14 – 10

= 7,14V

V_T.H. =v_abdominales = 7,14 voltios

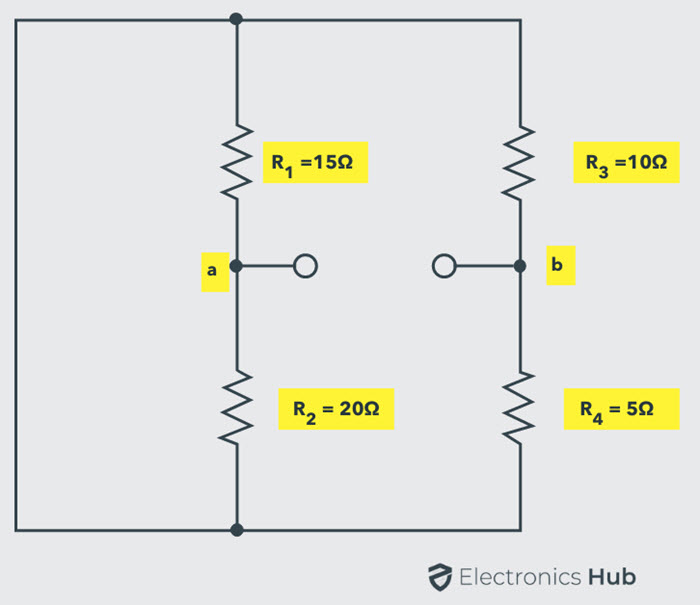
Calcule la resistencia equivalente de Thevenin R._T.H. Reemplazando la fuente de alimentación con su resistencia interna (aquí asumimos que la resistencia interna de la fuente de voltaje es cero, por lo que estará en cortocircuito).

La resistencia equivalente de Thevenin o la resistencia entre los terminales ab es:

R_T.H. =Amor= [R1R2 / (R1 + R2)] + [R3R4 /(R3 + R4)]

= [(15 × 20) / (15 + 20)] + [(10 × 5) / (10+ 5)]

= 8,57 + 3,33

R_T.H. = 11,90 ohmios

A continuación se muestra el circuito equivalente de Thevenin con el valor calculado anteriormente y la resistencia de carga reconectada.

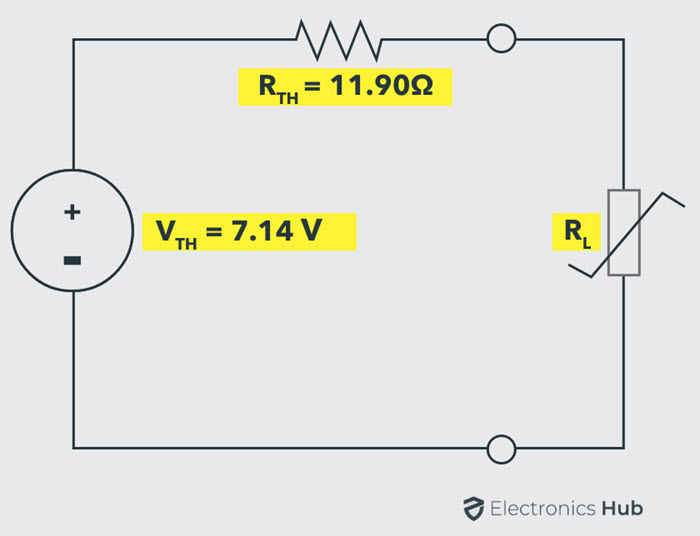
Del teorema de transferencia de máxima potencia, R_l el valor debe ser igual a R_T.H. Proporciona máxima potencia a la carga.

por lo tanto, R_l =R_T.H.= 11,90 ohmios

La potencia máxima transferida bajo esta condición es

PAG_máx. =v²_T.H. /4R_T.H.

= (7,14)² / (4 × 11,90)

= 50,97 / 47,6

= 1,07 vatios

Aplicar la máxima transferencia de energía a los circuitos de CA

La red de CA siguiente consta de una impedancia de carga Z._l Tanto la parte reactiva como la resistiva se pueden cambiar. Por lo tanto, es necesario determinar el valor de impedancia de carga y el valor de potencia máxima al que la fuente entregará la potencia máxima.

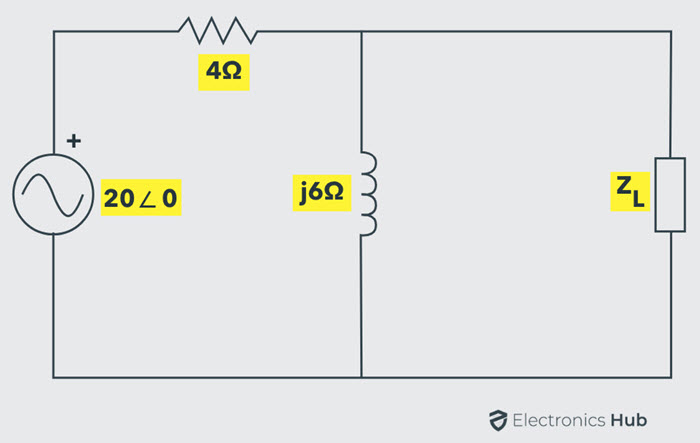
Para encontrar el valor de la impedancia de carga, primero encuentre el circuito equivalente de Thevenin entre los terminales de carga. Para encontrar el voltaje de Thevenin, desconecte la impedancia de carga como se muestra en la siguiente figura.

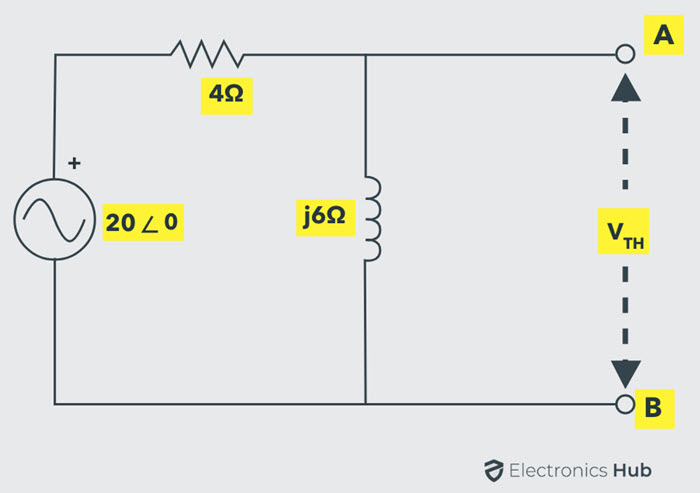
Según la ley del divisor de voltaje,

V_T.H. = 20∠0 × [j6 / (4 + j6)]

= 20∠0 ×[6∠90 / 7.21∠56.3]

= 20∠0 × 0,825∠33,7

V_T.H. = 16,5∠33,7V

Cuando la fuente de voltaje está en cortocircuito, la impedancia equivalente de Thevenin del circuito se calcula como se muestra en la figura.

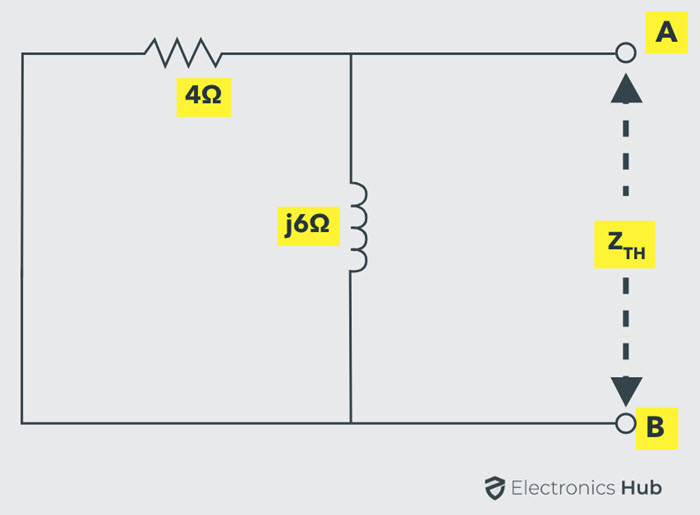
por lo tanto,

z_T.H. = (4 × j6) / (4 + j6)

= (4 × 6∠90) / (7,21∠56,3)

= 3,33∠33,7 0r 2,77 + j1,85 ohmios

Por tanto, el circuito equivalente de Thevenin entre los terminales de carga es:

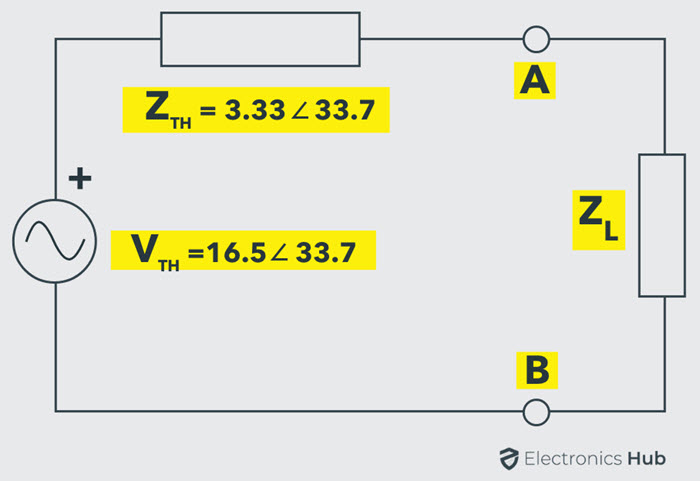
Por lo tanto, para transferir la máxima potencia a la carga, el valor de la impedancia de la carga debe ser:

z_l =Z_T.H.

= 2,77 – j1,85 ohmios

Potencia máxima entregada, P_máx.

=v²_T.H. /4R_T.H.

= (16,5)²/4(2,77)

= 272,25 / 11,08

= 24,5W

Aplicación práctica del teorema de máxima transferencia de potencia.

Consideremos un ejemplo práctico de un altavoz con una impedancia de 8 ohmios. Está impulsado por un amplificador de audio con una impedancia interna de 500 ohmios. El circuito equivalente de Thevenin también se muestra en la figura.

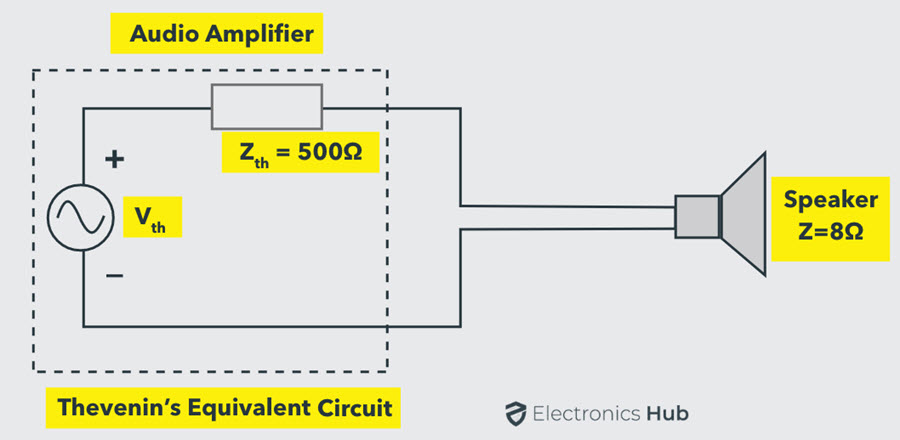
Según el teorema de transferencia de potencia máxima, si la impedancia de carga es de 500 ohmios (igual que la impedancia interna), la potencia será máxima en la carga. De lo contrario, la resistencia interna debe cambiarse a 8 ohmios para lograr las condiciones máximas de transferencia de potencia. Sin embargo, ninguno de los dos se puede cambiar.

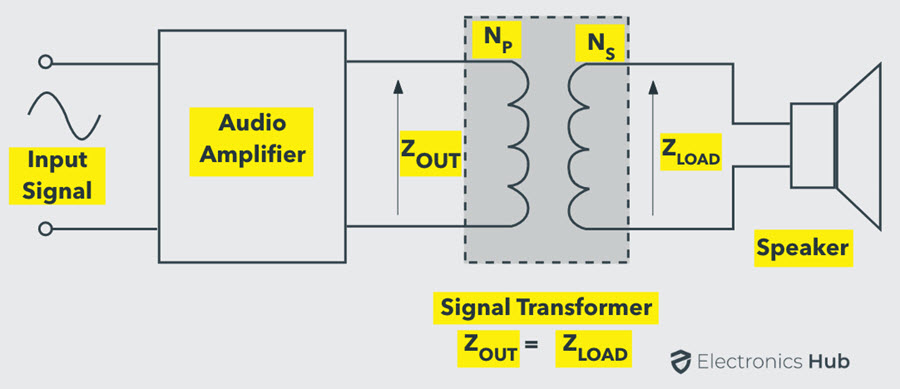
Por lo tanto, ésta es una condición de desajuste de impedancia que se puede superar utilizando un transformador de adaptación de impedancia con una relación de conversión de impedancia de 500:8.