Al analizar circuitos de CC, normalmente se utilizan una variedad de métodos, como la ley de Ohm, teoremas de redes y otras herramientas de simplificación de circuitos. El análisis de circuitos de CC se realiza principalmente para determinar cantidades desconocidas como voltaje, corriente, resistencia y potencia asociadas con uno o más elementos de un circuito electrónico. Como ley fundamental para simplificar circuitos, la ley de Ohm define una relación lineal entre voltaje, corriente y resistencia. Cuénteme más sobre la ley de Ohm.
Tabla de contenido
Ley de Ohm
Esta es la ley básica y más importante que examina la relación entre voltaje, corriente y resistencia en los circuitos eléctricos. Afirma que a una temperatura determinada, la corriente que fluye a través de un circuito es directamente proporcional al voltaje o diferencia de potencial a través de ese circuito.
En forma algebraica, V∝ I
V = IR
dónde
I es la corriente que fluye por el circuito, medida en amperios.
V es el voltaje aplicado a través del circuito, medido en voltios.
R es una constante de proporcionalidad llamada resistencia y se mide en ohmios.
Esta resistencia también se especifica en kiloohmios, megaohmios, etc.
Por tanto, la ley de Ohm establece que el flujo de corriente en un circuito es directamente proporcional al voltaje e inversamente proporcional a la resistencia en el circuito. La ley de Ohm se puede aplicar a componentes individuales o a circuitos completos.
Matemáticamente, actual, I = V/R
Voltaje, V = IR
Resistencia, R = V/I
Volver a la cima
triángulo de la ley de ohm
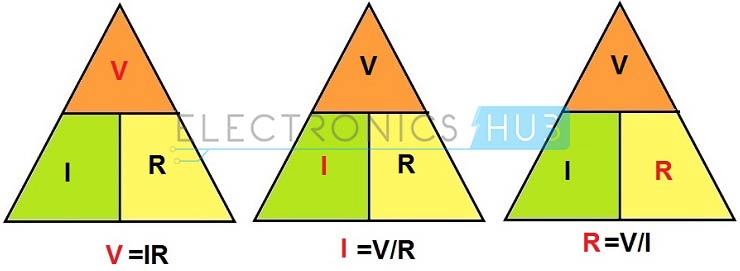
La siguiente disposición muestra que la relación entre diferentes cantidades en la ley de Ohm se llama triángulo de la ley de Ohm. Esta es una forma sencilla de explicar y recordar la relación entre voltaje, corriente y resistencia.
El diagrama anterior muestra el triángulo de la ley de Ohm, donde los términos individuales como voltaje, corriente y resistencia y sus fórmulas se expresan a partir de la ecuación básica de la ley de Ohm. En la figura anterior, un parámetro se calcula a partir de los dos parámetros restantes. Por lo tanto, podemos concluir que para cualquier voltaje aplicado, si la resistencia es alta, la corriente será menor, y si la resistencia es baja, la corriente aumentará.
Volver a la cima
energia electrica
La potencia indica la velocidad a la que un circuito transfiere energía. La potencia se mide en vatios. Esta potencia se disipa cuando el voltaje hace que la corriente fluya a través del circuito.
Por tanto, la potencia es el producto del voltaje y la corriente.
Matemáticamente, P = VI
De la ley de Ohm, V = IR y I = V/R
Sustituir en la ecuación de potencia.
P = yo2 R
P = V2/R
Por lo tanto, potencia, P =VI o I2 R o V2/R
Estas son las tres fórmulas básicas para determinar la potencia en un circuito. Por tanto, si conocemos alguna de las dos cantidades, podemos calcular la potencia.
Volver a la cima
triangulo de poder
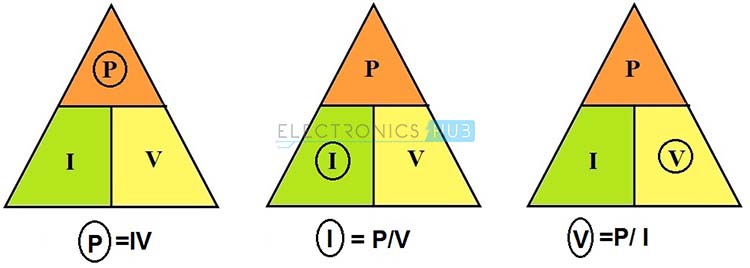
Similar al triángulo de la ley de Ohm, el siguiente diagrama muestra un triángulo de potencia que muestra la relación entre potencia, voltaje y corriente. Las ecuaciones de los parámetros individuales se pueden recuperar fácilmente en este diagrama. Redondeamos el parámetro que se está midiendo y lo ocultamos, y las posiciones de los dos parámetros restantes nos dan la ecuación para encontrar el parámetro oculto o redondeado, como se muestra en la imagen a continuación.
Volver a la cima
gráfico circular de la ley de ohm
Antes de los dos conceptos anteriores, existe otra forma de encontrar parámetros de circuito utilizando la ley de Ohm: el gráfico circular de la ley de Ohm. El gráfico circular de la ley de Ohm le permite recordar fácilmente todas las ecuaciones de voltaje, corriente, resistencia y potencia necesarias para simplificar circuitos eléctricos simples o complejos.
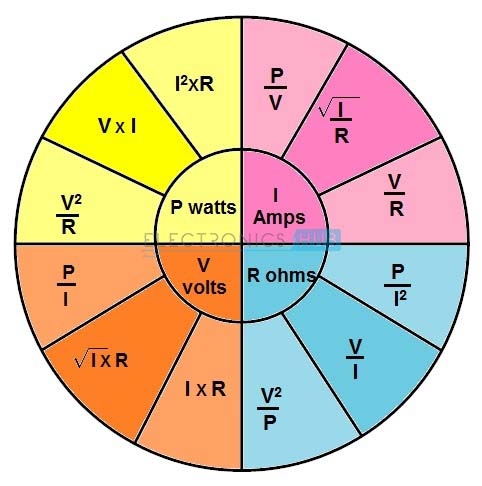
La figura anterior muestra un gráfico circular que muestra la relación entre potencia, voltaje, corriente y resistencia. Esta tabla se divide en cuatro unidades: potencia, voltaje, resistencia y corriente. Cada unidad consta de tres ecuaciones con dos valores conocidos para cada ecuación. A partir del gráfico, puede utilizar una de las tres fórmulas disponibles para determinar cada parámetro del circuito.
Volver a la cima
Representación gráfica de la ley de Ohm.
Para comprender mejor este concepto, a continuación se muestra una configuración experimental donde una fuente de voltaje ajustable con seis celdas (2 V cada una) se conecta a una resistencia de carga a través de un interruptor selector de voltaje. También se conectan al circuito instrumentos de medición como voltímetros y amperímetros para medir el voltaje y la corriente en el circuito.
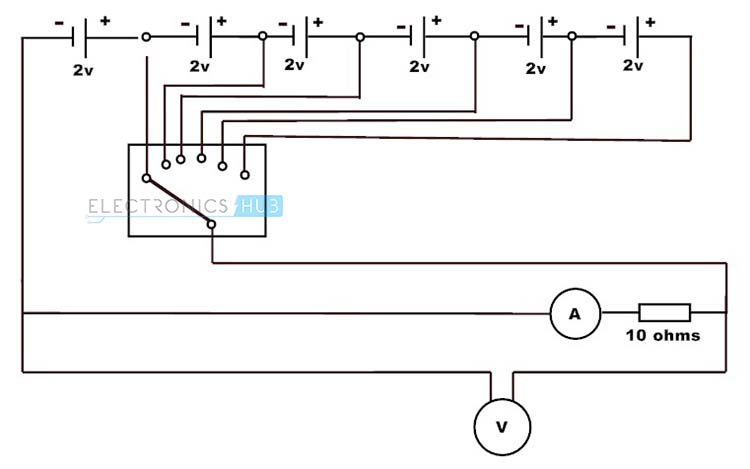
Primero conecte la resistencia de 10 ohmios y coloque el interruptor selector en la posición 1. Entonces I = V/R, o I = 2/10 = 0,2 A, por lo que el amperímetro indica 0,2 A y el voltímetro indica 2 V. Luego, cambie la posición del interruptor selector a la segunda celda, aplique 4 V a través de la carga y observe la lectura del amperímetro. Cuando el selector cambia en pasos desde la primera posición a la última posición, los valores actuales como 0,2, 0,4, 0,6, 0,8, 1, 1,2 para los valores de voltaje 2, 4, 6, 8, 10, 12 respectivamente. Puede ser obtenido.
De manera similar, coloque una resistencia de 20 ohmios en lugar de la resistencia de 10 ohmios y siga los mismos pasos anteriores. Se obtienen valores de corriente de 0,1, 0,2, 0,3, 0,4, 0,5 y 0,6 para valores de voltaje de 2, 4, 6, 8, 10 y 12 V, respectivamente. Trace una gráfica de estos valores como se muestra a continuación.
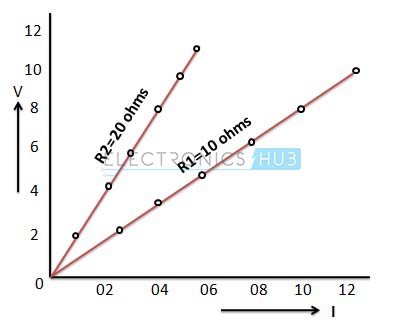
En el gráfico anterior, para un voltaje determinado, a medida que aumenta la resistencia, la corriente disminuye. Considere el caso en el que se aplica un voltaje de 12 V y si la resistencia es de 10 ohmios, el valor actual es 1,2 A, y si la resistencia es 20 ohmios, el valor actual es 0,6 ohmios. De manera similar, si fluye la misma corriente, cuanto mayor sea la resistencia, mayor será el voltaje. De los resultados anteriores, si la resistencia es constante, la relación entre voltaje y corriente es constante. Por lo tanto, la relación entre voltaje y corriente es lineal y la pendiente de esta curva lineal se vuelve más pronunciada a medida que aumenta la resistencia.
Volver a la cima
ejemplo de la ley de ohm
Considere el circuito a continuación donde se conecta una batería de 6 V a una carga de 6 ohmios. Conecte un amperímetro y un voltímetro al circuito para medir realmente la corriente y el voltaje. Sin embargo, usando la ley de Ohm, podemos encontrar la corriente y la potencia de la siguiente manera:
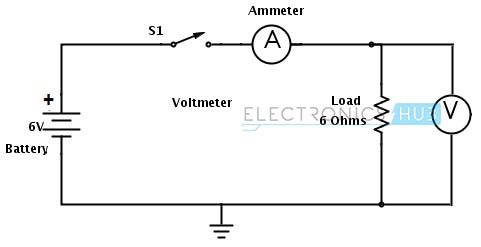
De la ley de Ohm
V = IR
Yo = V/R
yo = 6/6
yo = 1 amperio
Potencia, P = VI
P = 6×1
P = 6 vatios
Sin embargo, en realidad, el amperímetro no da un valor exacto debido a la resistencia interna de la batería. Incluyendo la resistencia interna de la batería (suponiendo que la resistencia interna de la batería sea 1 ohmio), el valor actual se calcula como:
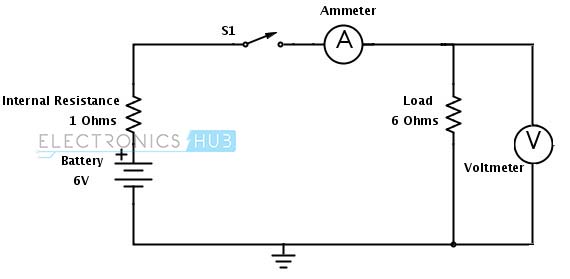
La resistencia total del circuito es 6 +1 = 7 ohmios.
Corriente, I = V/R
yo = 6/7
Yo = 0,85 amperios
Volver a la cima
circuito de faros de coche
El siguiente diagrama muestra el circuito de los faros de un automóvil sin el circuito de control. Aplicando la ley de Ohm, podemos encontrar la corriente que fluye por cada luz. Cada luz suele estar conectada en paralelo a una batería, por lo que si alguien la daña, las otras luces seguirán encendiéndose. Una batería de 12 V alimenta estas lámparas en paralelo. La resistencia de las lámparas es de 2,4 cada una (considerada en este caso).
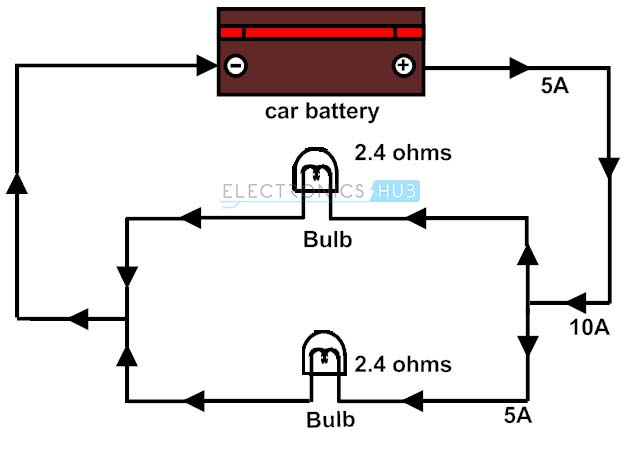
La resistencia total del circuito es R = R1x R2/ (R1 + R2) ya que están en paralelo.
R = 5,76/ 4,8 = 1,2
En este caso, la corriente que circula por el circuito es I = V/R.
Yo = 12/1,2
I=10A.
La corriente que circula por cada lámpara es I1 = I2 = 5 A (debido a la misma resistencia)
Volver a la cima
Ley de Ohm para circuitos de CA.
En general, la ley de Ohm también se puede aplicar a circuitos de CA. También se considera la reactancia de la carga si la carga es inductiva o capacitiva. Por lo tanto, con algunas modificaciones a la ley de Ohm para tener en cuenta los efectos de la reactancia, también se puede aplicar a circuitos de CA. La inductancia y capacitancia de CA crean un ángulo de fase significativo entre el voltaje y la corriente. Además, la resistencia de CA se llama impedancia y está representada por Z.
Por lo tanto, la ley de Ohm para un circuito de CA viene dada por:
E = IZ
Yo = E/Z
Z = E/I
donde E es el voltaje del circuito de CA
Estoy presente;
Z es la impedancia.
Todos los parámetros de la ecuación anterior están en forma compleja, incluido el ángulo de fase. De manera similar al gráfico circular para un circuito de CC, a continuación se muestra el gráfico circular de la ley de Ohm para un circuito de CA.
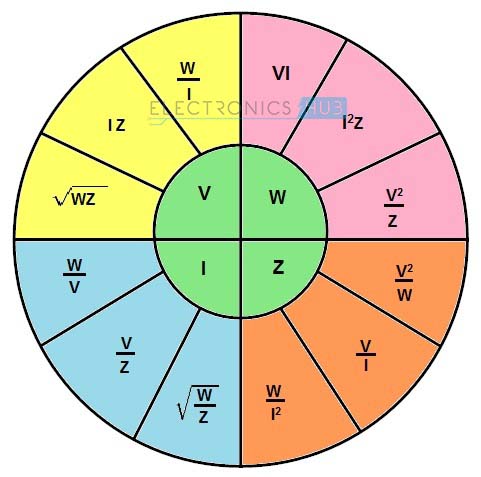
Volver a la cima
Ejemplo de ley de Ohm (circuito CA)
Considere el circuito a continuación donde una carga de CA (una combinación de resistiva e inductiva) está conectada a una fuente de alimentación de CA de 10 V y 60 Hz. La resistencia de carga es de 5 ohmios y la inductancia es de 10 mH.
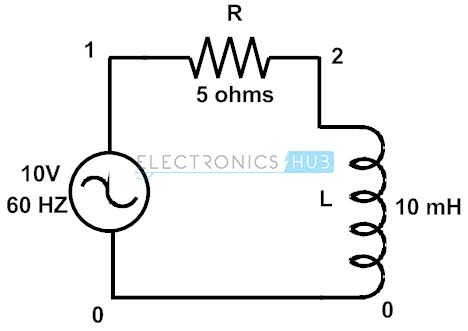
Entonces el valor de impedancia de la carga, Z = R + jXl
Z = 5 + j (2∏×f × L)
Z = 5+ j (2×3,14× 60×10× 10-3)
Z = 5 + j3,76 ohmios, o 6,26 ohmios en el ángulo de fase -37,016
La corriente que circula por el circuito es
Yo = V/Z
= 10/ (5+ j3,76)
= 1,597A en ángulo de fase -37,016
Volver a la cima