Como vimos en un artículo anterior, para simplificar el circuito combinamos resistencias en serie y en paralelo para reducir la complejidad del circuito. Además, las técnicas de transformación de fuentes se utilizan a menudo para analizar circuitos. Sin embargo, estas técnicas no son aplicables a todos los tipos de redes.
[adsense1]
Muchos circuitos constan de tres redes terminales, como una red en estrella (Y) o en estrella o en T (T) y una red en delta o pi. Estas redes pueden ser parte de redes más grandes o ocurrir de forma independiente. Los campos de aplicación de estas redes incluyen redes trifásicas, redes de adaptación, filtros eléctricos, etc. Estas redes se simplifican utilizando otra técnica útil llamada transformación estrella-delta.
Tabla de contenido
Red Star y Red Delta
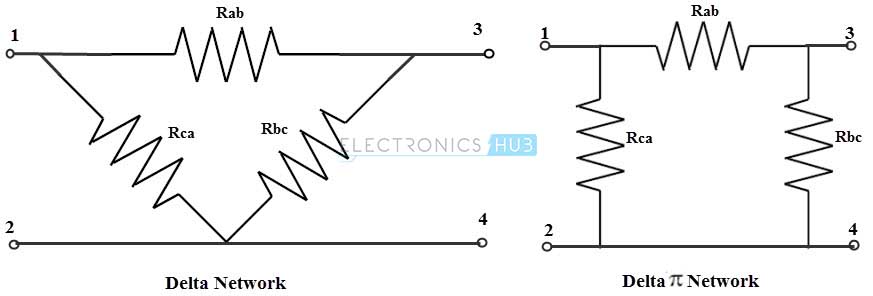
Una conexión en estrella conecta componentes de manera que un extremo de todas las resistencias o componentes esté conectado a un punto común. La disposición de las tres resistencias hace que esta red en estrella se parezca a la letra Y, por lo que esta red también se llama red Y o red Y. El equivalente de esta conexión en estrella se puede reescribir como una red T (red de cuatro terminales), como se muestra en el siguiente diagrama. La mayoría de los circuitos eléctricos constan de esta red en forma de T.
Una conexión delta conecta el extremo de cada componente o bobina con el inicio de otro componente o bobina. Esta es una conexión en serie de tres componentes conectados para formar un triángulo. El nombre indica que la conexión se parece al alfabeto delta (Δ). La red delta equivalente se puede volver a dibujar para que se parezca al símbolo Pi (o una red de cuatro terminales), como se muestra en la figura. Por lo tanto, esta red también se llama red Pi.
Volver a la cima
[adsense2]
Conversión delta a estrella
La conversión de estrella-triángulo o delta-estrella se puede lograr cuando pares de terminales similares tienen la misma impedancia. Esta transformación elimina nodos y produce una red equivalente.
Describe la conversión delta a estrella. Considere que Rab, Rbc y Rca son las tres resistencias en serie de una red en delta, y Ra, Rb y Rc son las tres resistencias de una red en estrella.
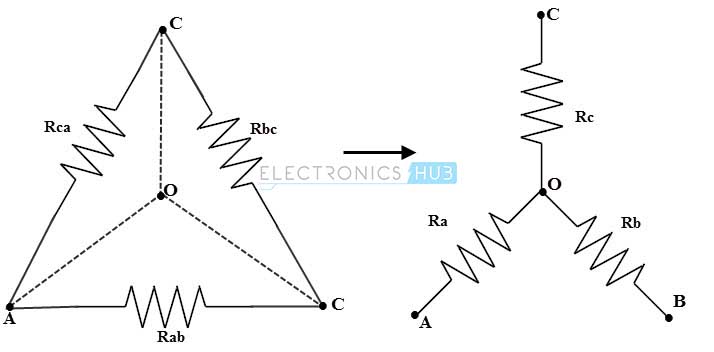
Esta red equivalente en estrella y triángulo producida después de la conversión tiene la misma resistencia cuando se mide entre pares similares de terminales.
Considere el diagrama de arriba. La resistencia equivalente entre los terminales a y c es:
Ra+Rc = Rca ||(Rab + Rbc )
Ra+Rc = Rca * (Rab + Rbc)/(Rab + Rbc + Rca) ……………………(1)
La resistencia equivalente entre el terminal c y el terminal b es:
Rb+Rc=Rbc || (Rab + Rca)
Rb+Rc = Rbc * (Rab + Rca)/(Rab + Rbc + Rca) ……………………(2)
Y entre la terminal b y la terminal a,
Rb+Ra = Rab ||(Rca + Rbc )
Rb+Ra = Rab * (Rca + Rbc)/(Rab + Rbc + Rca) ……………………..(3)
Combinando las ecuaciones 1, 2 y 3 anteriores, obtenemos:
Ra + Rb + Rc = (RabRbc + RbcRca + RcaRab)/(Rab + Rbc + Rca) ……………(4)
Restar la Ecuación 2 de la Ecuación 4 produce:
Ra = (Rab Rca)/(Rab + Rbc + Rca)
Restar la Ecuación 1 de la Ecuación 4 produce:
Rb = (Rab Rbc)/(Rab + Rbc + Rca)
Restar la Ecuación 3 de la Ecuación 4 produce:
Rc = (Rbc Rca)/(Rab + Rbc + Rca)
Estos Ra, Rb y Rc son los tres valores de resistencia de la red en estrella convertida a partir del circuito equivalente en delta.
Ra = (Rab Rca)/(Rab + Rbc + Rca)
Rb = (Rab Rbc)/(Rab + Rbc + Rca)
Rc = (Rbc Rca)/(Rab + Rbc + Rca)
Observando las tres ecuaciones anteriores, para un terminal determinado, la resistencia equivalente en la red en estrella es el producto de las dos resistencias conectadas al mismo terminal (en delta) dividido por la suma de las resistencias totales en la red en delta. Se puede decir que es equivalente a algo. .
Volver a la cima
ejemplo:
Teniendo en cuenta el diagrama siguiente, convierta el delta con valores Ra = 20 ohmios, R2 = 30 ohmios, R3 = 50 ohmios a un circuito en estrella o en estrella.
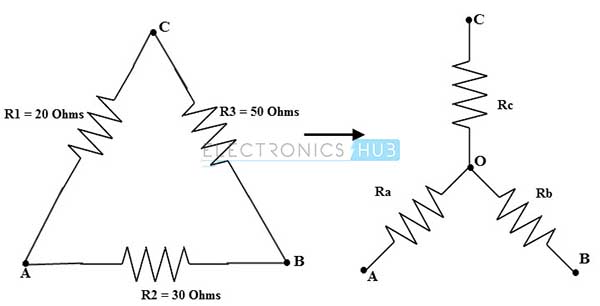
Para la conversión delta a estrella, la ecuación de resistencia equivalente (para este problema) es:
Ra = (R1 R2)/(R1 + R2 + R3)
Rb = (R2 R3)/(R1 + R2 + R3)
Rc = (R1 R3)/(R1 + R2 + R3)
Por tanto, resistencia total Rt = (R1 + R2 + R3)
= 20 + 30 + 50
= 100 ohmios
Ra = (R1 R2)/(R1 + R2 + R3)
= (20 X 30) /100
= 6 ohmios
De manera similar Rb = (R2 R3)/(R1 + R2 + R3)
= (30 X 50) /100
= 15 ohmios
Rc = (R1 R3)/(R1 + R2 + R3)
= (50×20)/100
= 10 ohmios
Volver a la cima
Conversión de estrella a delta
Utilice las mismas expresiones de resistencia para estrellas que Ra, Rb y RC, y utilice las mismas expresiones de resistencia para delta que Rab, Rbc y Rca. Considere la red de resistencias en estrella que se muestra a continuación. Aquí, la corriente que fluye a través de la resistencia Ra viene dada por:
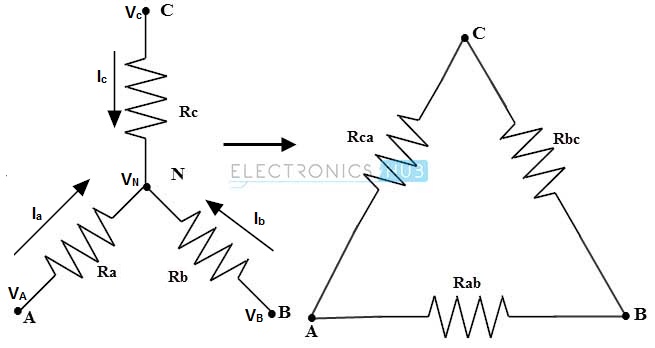
Ia = (Va – Vn) / Ra ………..(1)
La aplicación de KCL en el nodo N de una red en estrella da como resultado:
(Va – Vn) /Ra + (Vb – Vn) /Rb + (Vc – Vn) /Rc
Vn [(1/Ra) + (1/Rb) + (1/Rc)] = (Va/Ra) + (Vb/Rb) + (Vc/Rc)
Vn = [(Va/Ra) + (Vb/Rb) + (Vc/Rc)] / [(1/Ra) + (1/Rb) + (1/Rc)] …(2)
En una red delta, la corriente en el punto A es:
Ia = (Vab /Rab) + (Vac / Rac) ……(3)
De las ecuaciones 1 y 3 obtenemos:
(Va – Vn) / Ra = (Vab /Rab) + (Vac / Rac) …………………..(4)
Sustituir el valor Vn de la Ecuación 2 en la Ecuación 4 se simplifica a:
Rab = Ra + Rb + ((RaRb)/Rc)
Rac = Ra + Rc + ((RaRc)/Rb)
De manera similar, Ib de la red en estrella es
Ib = (Vb – Vn) / Rb ………..(5)
dentro de la red delta
Ib = (Vbc /Rbc) + (Vba / Rba) ………………(6)
Al igualar las ecuaciones de 5 y 6,
(Vb – Vn) / Rb = (Vbc /Rbc) + (Vba / Rba) ………………..(7)
Sustituyendo la Ecuación 2 en la Ecuación 7 y simplificándola se obtiene:
Rbc = Rb + Rc + ((RbRc)/Ra)
Por lo tanto, la ecuación requerida para convertir una red en delta en una red en estrella o en Y equivalente es:
Rab = Ra + Rb + ((RaRb)/Rc) = ( RaRb + RbRc + RbRc )/Rc
Rbc = Rb + Rc + ((RbRc)/Ra) = ( RaRb + RbRc + RbRc )/Ra
Rac = Ra + Rc + ((RaRc)/Rb) = (RaRb + RbRc + RbRc )/Rb
Observando las tres ecuaciones anteriores, la resistencia delta equivalente entre dos terminales dados es la suma de las dos resistencias conectadas a esos terminales (forma de estrella), más el producto de las mismas dos resistencias, más las restantes o Podemos decir que es igual a valor dividido por la tercera estrella. resistencia.
Volver a la cima
ejemplo:
Convierta un circuito en estrella o estrella en un circuito en triángulo considerando el siguiente diagrama. Los valores de resistencia de la red en estrella se dan como R1= 10 ohmios, R2= 5 ohmios, R3 = 20 ohmios.
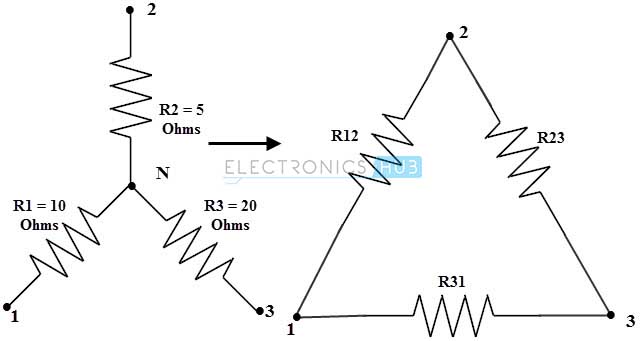
Para la conversión de estrella o estrella a delta, la ecuación de resistencia equivalente (para este problema) es:
R12 = R1 + R2 + ((R1R2)/R3)
R23 = R2 + R3 + ((R2R3)/R1)
R31 = R1 + R3 + ((R1R3)/R2)
Simplificando la ecuación anterior, obtenemos el término numerador común como:
R1R2 + R2R3 + R1R3
= 10×5 + 10×20 + 20×5
= 350 ohmios
Por lo tanto, R12 = 350/R3
= 350/20
= 17,5 ohmios
R23 = 350/R1
= 350/10
= 35 ohmios
R31=350/R2
= 350/5
= 70 ohmios
Volver a la cima