Análisis nodal

introducción

El concepto principal detrás del análisis nodal es que para un circuito dado, si se conocen los voltajes de los nodos, todas las corrientes derivadas asociadas con ese circuito se pueden determinar inmediatamente. Como sabes, usamos KCL para encontrar los voltajes de los nodos. Esta técnica reduce el número de ecuaciones y simplifica el circuito porque los voltajes de los nodos se consideran variables en lugar de los voltajes de los elementos en el circuito. En el método de análisis de nodos, si todos los nodos están disponibles, un nodo se considera el nodo de referencia (potencial cero) y se representa como un terminal de tierra. A los nodos desconocidos restantes se les asignan voltajes relativos al voltaje del nodo de referencia.

Aplique KCL a cada nodo en el circuito dado, excluyendo el nodo de referencia. Supongamos que si hay N nodos en un circuito dado, tenemos N-1 ecuaciones simultáneas para encontrar los N-1 voltajes de nodo desconocidos.

Volver a la cima

Procedimiento de análisis del método de análisis nodal.

1) Convierta las fuentes de voltaje en el circuito dado en fuentes de corriente y verifique si se pueden convertir.

2) Identificar los nodos presentes en un circuito determinado, asignar un nodo como nodo de referencia y etiquetar otros nodos como voltajes de nodo desconocidos con respecto a este nodo de tierra o de referencia.

3) Asigne una dirección de corriente a cada rama del circuito dado (esta es una decisión arbitraria).

4) Cree las ecuaciones nodales aplicando KCL a los N-1 nodos y expresando las corrientes de las ramas como voltajes asignados a los nodos.

5) Resuelva las ecuaciones simultáneas de los nodos para encontrar los voltajes de los nodos y finalmente encuentre las corrientes de las ramas. El número de ecuaciones de nodos es igual al número de nodos menos 1 (porque se hace referencia a un nodo).

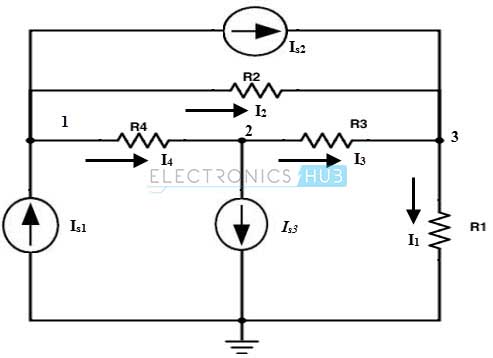
Considere el circuito de CC a continuación. En este circuito, las corrientes derivadas se determinan mediante análisis nodal.

Como primer paso en el análisis de nodos, debemos seleccionar un nodo de referencia que esté conectado a potencial cero o potencial de tierra, como se muestra a continuación.

A continuación, aplique la ley de corriente de Kirchhoff (KCL) a cada nodo del circuito excepto al nodo de referencia. Aplicar KCL en el nodo 1:

Is1 – Is3 – I4 – I2 = 0

Is1 – Is3 – {(V1 – V2)/R4} – {(V1- V3)/R2} = 0

Is1 – Is3 = V1 { (1/R2) + (1/R4)} – V2 (1/R4) – V3 (1/R2)

Is1- Is3 = G11 V1 – G12 V2 – G13 V3 …………………..(1)

donde G1i es la suma de la conductancia total del primer nodo. (Sabemos que 1/ R = G)

Aplicar KCL en el nodo 2:

I4 – Is2 – I3 = 0

{(V1 – V2)/R4} – Is2 – {(V2 – V3)/R3} = 0

– Is2 = – V1 (1/R4) + V2 { (1/R3) + (1/R4)} – V3 (1/R3)

– Is2 = – G21 V1 – G22 V2 – G23 V3 ………………………(2)

La aplicación de KCL en el nodo 3 produce los siguientes resultados:

Is3 + I2 + I3 – I1 = 0

Is3 + {(V1 – V3)/R2} – {(V2 – V3)/R3} – V3 (1/R1) = 0

Is3 = – V1 (1/R2) – V2 (1/R3) + V3 { (1/R1) + (1/R2) + (1/R3)}

Is3 = – G31 V1 – G32 V2 + G33 V3…………………………..(3)

De manera similar, podemos escribir la ecuación KCL para el i-ésimo nodo.por lo tanto

∑ Iii es igual a la suma algebraica de todas las corrientes conectadas al iésimo nodo. donde i = 1, 2, 3…N y N = n-1 (n es el número total de nodos presentes en el circuito).

Gii = conductancia total conectada al i-ésimo nodo.

Gij = suma de conductancias conectadas entre el nodo i y el nodo j.

Resolviendo las tres ecuaciones anteriores, podemos obtener el voltaje de rama en cada nodo, lo que nos permite calcular la corriente de rama.

Volver a la cima

ejemplo

Determine los voltajes y corrientes de los nodos para cada rama utilizando la técnica de análisis de nodos para el circuito dado.

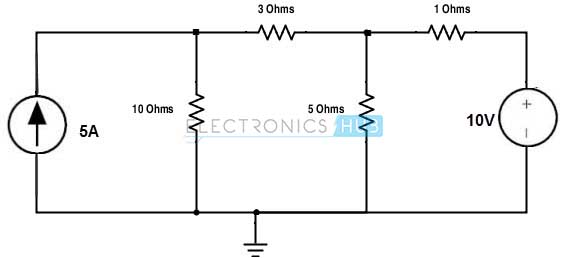
El circuito dado contiene una fuente de voltaje. Se puede convertir a una fuente actual o analizar directamente sin conversión. Ahora calculemos los voltajes de los nodos sin realizar ninguna conversión.

El primer paso en el análisis de nodos es seleccionar y etiquetar los nodos que existen dentro de un circuito particular. Seleccionar el nodo inferior como nodo de referencia da como resultado dos nodos separados en el circuito dado. Por lo tanto, estos nodos están etiquetados como V1 y V2 como se muestra en la imagen siguiente. También muestra la dirección actual en cada rama.

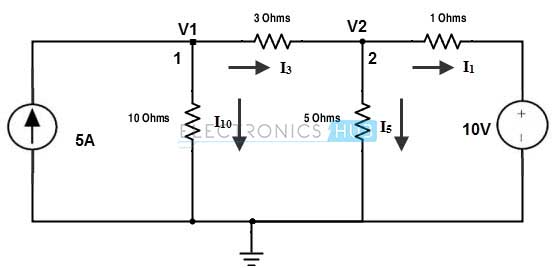
Aplicar KCL en el nodo 1:

5 = I3 + I10

5 = (V1/10) + (V1 – V2/3)

13V1 – 10V2 = 150……(1)

Aplicar KCL en el nodo 2:

I3 = I5 + I1

(V1 – V2/3) = (V2/5) + (V2 – 10/1)

5V1 – 23V2 = -150 ……..(2)

Resolviendo las dos ecuaciones anteriores se obtiene:

V1 = 19,85 voltios y V2 = 10,9 voltios

La corriente en cada rama viene dada por:

I10 = V1/10

= 19,85/10 = 1,985

I3 = V1 – V2/3

= 19,85 – 10,9/3

= 2,98A

I5 = V2/5

= 10,9/5

= 2,18A

I1 = V2 – 10

= 10,9 – 10

= 0,9A

Volver a la cima

Concepto de supernodo

Aplicar el análisis nodal puede resultar difícil cuando existe una fuente de voltaje entre dos ramas de un circuito. Una forma de resolver este problema es aplicar tecnología de supernodos. En la tecnología de supernodo, las fuentes de voltaje conectadas entre dos nodos adyacentes se ponen en cortocircuito para reducir los dos nodos y formar un supernodo.

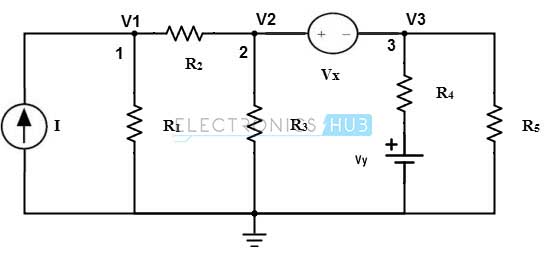
Considere el ejemplo anterior donde la fuente de voltaje está conectada entre los nodos 2 y 3. Los cálculos se vuelven aún más difíciles cuando se analizan circuitos que utilizan fuentes de voltaje. Cortar dos y tres nodos para crear un supernodo facilitará el análisis de este circuito.

Aplicando la actual ley de Kirchoff al nodo 1, obtenemos:

Yo = (V1/R1) + ((V1-V2)/R2) ……(1)

La técnica del supernodo se puede aplicar a ciertos circuitos acortando el segundo y tercer nodo y aplicando KCL.

((V2-V1)/R2) + (V2/R3) + ((V3-Vy)/R4) + (V3/R5) = 0

Además, el voltaje de la fuente de voltaje está dado como:

Vx = V2 – V3

A partir de las tres ecuaciones anteriores, podemos encontrar fácilmente los tres voltajes desconocidos en el circuito.

Volver a la cima

Ejemplo de supernodo

Considere el circuito siguiente y utilice la técnica del supernodo para encontrar los tres voltajes de nodo desconocidos V1, V2 y V3.

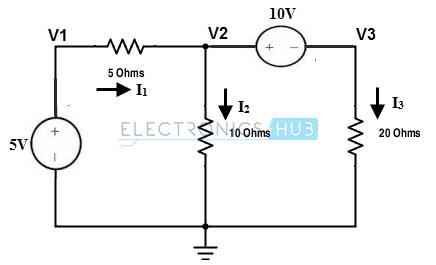
En el nodo 1, la fuente está conectada al nodo de referencia, por lo que V1 es 5V.

V1 = 5V

Un supernodo está formado por los nodos 2 y 3. La aplicación de KCL a este supernodo produce los siguientes resultados:

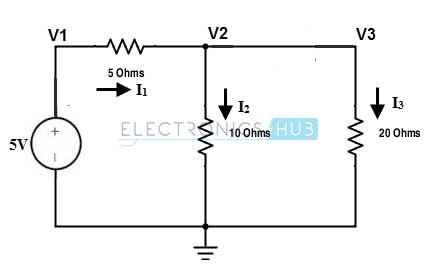
i1 = i2 + i3

(V1 – V2)/5 = (V2 / 10) + (V3/20)…………..(1)

Además, el KVL del supernodo es

V2 – V3 = 10……………… (2)

Al resolver la ecuación anterior se obtiene V2 = 4,29 V y V3 = -5,71 V.

Volver a la cima