El análisis de circuitos le permite analizar circuitos simples utilizando herramientas de análisis básicas como la ley de Ohm, KVL y KCL. Sin embargo, para circuitos complejos que constan de diferentes fuentes de control, además de esquemas en serie y paralelo, estas herramientas no son confiables. Por tanto, se utilizan técnicas de análisis de nodos y mallas (o bucles) para encontrar las variables de las ramas de dichos circuitos. Utilizando estos métodos clásicos, las variables del circuito como el voltaje y la corriente se determinan fácilmente en cualquier rama sin dificultades significativas. Echemos un vistazo más de cerca al análisis de malla.
Tabla de contenido
análisis de malla
Una malla es un bucle sin otros bucles en su interior. Las técnicas de análisis de malla utilizan corrientes de malla como variables en lugar de corrientes en los elementos para analizar el circuito. Por tanto, este método reduce absolutamente el número de ecuaciones a resolver. El análisis de malla aplica la ley de voltaje de Kirchhoff (KVL) para determinar corrientes desconocidas en un circuito determinado. El análisis de malla también se denomina método de corriente de malla o análisis de bucle. Después de encontrar la corriente de malla usando KVL, podemos usar la ley de Ohm para determinar el voltaje en cualquier lugar dentro de un circuito determinado.
Volver a la cima
Pasos para analizar el método de análisis de malla.
1) Compruebe si todas las fuentes de corriente en el circuito dado se pueden convertir en fuentes de voltaje.
2) Asigne una dirección de corriente a cada malla en un circuito determinado y siga la misma dirección en cada malla.
3) Aplique KVL a cada malla y simplifique la ecuación KVL.
cuatro) Si resolvemos el sistema de ecuaciones para diferentes mallas para obtener corrientes de malla, estas ecuaciones son exactamente iguales al número de mallas presentes en la red.
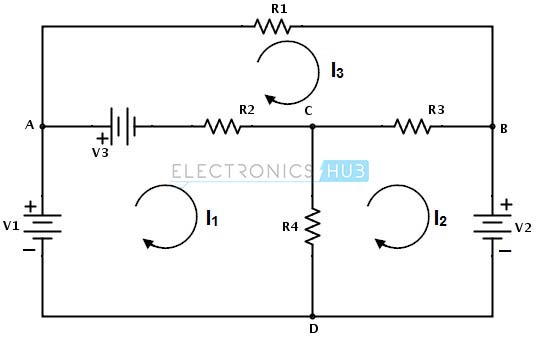
Para aplicar el análisis de corriente de malla de modo que se puedan encontrar las corrientes en diferentes mallas, considere el siguiente circuito de CC. En la imagen a continuación, hay tres mallas: ACDA, CBDC y ABCA, pero la ruta ABDA no es una malla. Como primer paso, a la corriente que fluye a través de cada malla se le asigna la misma dirección, como se muestra en la figura.
A continuación, debemos aplicar KVL en cada malla. La aplicación de KVL alrededor del primer bucle o malla da el siguiente resultado:
V1 − V3 − R2 ( I1 − I 3 ) − R4 ( I1 − I 2 ) = 0
V1 − V3 = I1 ( R2 + R4 ) − I2R4 − I3R2 ……………(1)
De manera similar, aplicar KVL alrededor de la segunda malla da como resultado:
−V2 − R3 (yo 2 − yo 3 ) − R4 (yo 2 − yo1 ) = 0
− V2 = − I1R4 + Yo 2 ( R3 + R4 ) − Yo 3 R3 …………………(2)
Y cuando aplicamos KVL alrededor de la tercera malla o bucle, obtenemos:
V3 − R1I 3 − R3( Yo 3 − Yo 2 ) − R2( Yo 3 − I1 ) = 0
V3 = − I1R2 − I2R3 + I3(R1 + R2 + R3) …………………(3)
Por lo tanto, resolviendo las tres ecuaciones anteriores, podemos obtener la corriente de malla para cada malla en un circuito determinado.
Volver a la cima
Ejemplos de problemas de análisis de malla:
Ejemplo 1:
Considere el siguiente ejemplo que utiliza el análisis de malla para encontrar el voltaje en una fuente de corriente de 12 A. En el circuito dado, todas las fuentes son fuentes de corriente.
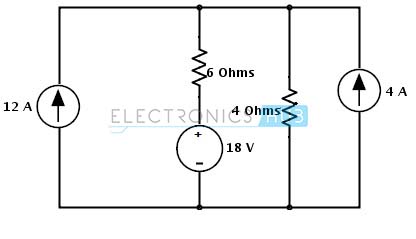
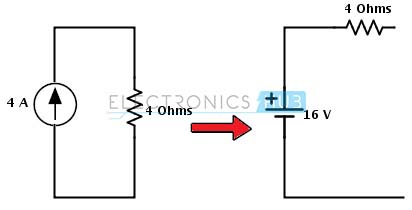
paso 1: En este circuito, existe la posibilidad de cambiar la fuente de corriente a una fuente de voltaje en el suministro correcto usando una resistencia en paralelo. Una fuente de corriente se convierte en una fuente de voltaje colocando una resistencia del mismo valor en serie con la fuente de voltaje, y el voltaje de esa fuente se determina como:
Vs = Rs
= 4×4 = 16 voltios
Paso 2: Asigne las corrientes de rama a sus respectivas ramas o bucles como I1 e I2 para representar la dirección de la corriente como se muestra a continuación.
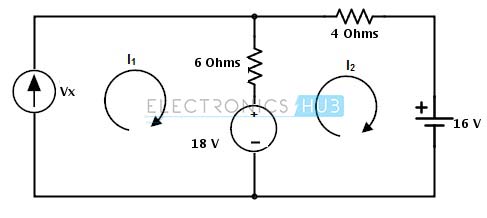
Paso 3: Aplica KVL a cada malla en el circuito dado.
malla -1:
Vx − 6 × (I1 − I2) − 18 = 0
Sustituir I1 = 12 A
Vx + 6I2 = 90…………………… (1)
Malla – 2:
18 − 6 × ( yo 2 − yo1 ) − 4 × yo 2 − 16 = 0
2 – 10 × I2 + 6(12) = 0
Yo2 = 74/10
= 7,4 amperios
Sustituyendo en la Ecuación 1, obtenemos:
Vx = 90 – 44,4
= 45,6 voltios
Ejemplo 2:
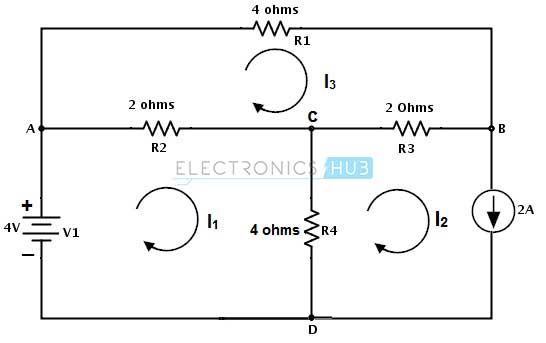
Considere el siguiente circuito que determina el voltaje entre las fuentes de corriente y la corriente derivada Iac. Asigne direcciones como se muestra a continuación. Tenga en cuenta que en el segundo bucle la corriente se asigna inversamente a la corriente de fuente.
Después de aplicar KVL a la primera malla, se ve así:
V1 − R2 ( Yo1 − Yo 3 ) − R4 ( Yo1 − Yo 2 ) = 0
4 – 2I1 − 2I3 − 4I1 − 4I2 = 0
-6I1 − 2I3 = 4 ………(1)
La aplicación de KVL a la segunda malla da como resultado lo siguiente:
−Vc − R4( Yo 2 − I1 ) − R3 ( Yo 2 − Yo 3 ) = 0
– Vc = 4I2 − 4I1 + 2I2 − 2I3 = 0
– Vc = – 4I1 + 6I2 – 2I3
Sin embargo, dado que I2 = -2 A,
– Vc = – 4I1 – 12 – 2 I3 …………….(2)
La aplicación de KVL a la tercera malla da como resultado:
− R1 yo 3 − R3 ( yo 3 − yo 2 ) − R2 ( yo 3 − yo 1 ) = 0
−4 I3 − 2I3 + 2I2 − 2I3 + 2I1 = 0
− 8I3 − 4 + 2I1 = 0 (sustituir I2 = -2 A)
2I1 − 8I3 = 4 ………………………(3)
Al resolver las ecuaciones 1 y 3 se obtiene I3 = -0,615 e I1 = 4,46.
Por tanto, tensión Vc = 4 (4,46) + 12 + 2(-0,615)
Vc = 28,61V
Además, corriente de rama Iac = I1-I3
Iac = 5,075 amperios
De manera similar, el análisis de malla se puede utilizar para encontrar todas las corrientes derivadas.
Volver a la cima
Análisis de súper malla
Como vimos en el Ejemplo 2, una de las ramas contiene una fuente actual. Luego, antes de aplicar el análisis de malla al circuito, asumimos un voltaje desconocido a través de la fuente de corriente y aplicamos el análisis de malla. Este es un enfoque muy difícil, pero se puede superar aplicando técnicas de supermalla.
Una supermalla se forma cuando dos mallas adyacentes comparten una fuente de corriente común y ninguna de estas mallas (adyacentes) contiene una fuente de corriente en sus bucles externos. Considere el siguiente circuito donde se forma una supermalla mediante un bucle alrededor de una fuente de corriente.
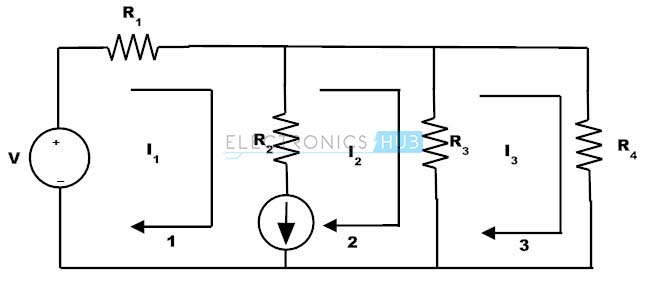
La fuente de corriente es común a las mallas 1 y 2, por lo que deben analizarse por separado. Para lograr esto, suponga que la rama que contiene la fuente de corriente es un circuito abierto y cree una nueva malla llamada supermalla.
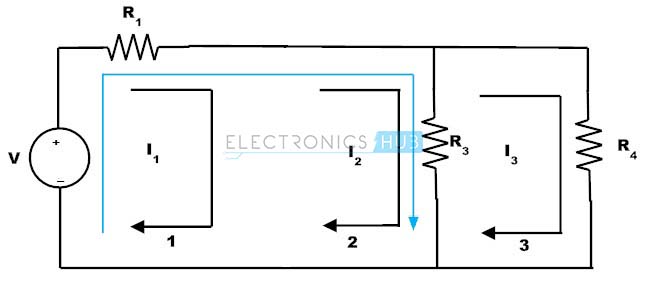
Escribe KVL en la supermalla obtenida.
V = I1R1 + (I2 – I3) R3
= I1R1 + I2R3 – I3R3
Aplicar KVL a la malla obtenida 3.
(I3 – I2) R3 + I3R4 = 0
La diferencia entre las dos corrientes de malla da la corriente de la fuente actual. Aquí, la dirección de la fuente de corriente es la dirección de corriente del bucle I1. Por lo tanto, dado que I1 es mayor que I2,
Yo = I1 – I2
Por lo tanto, utilizando estas tres ecuaciones de malla, podemos encontrar fácilmente las tres corrientes desconocidas en la red.
Volver a la cima
Ejemplo de análisis de supermalla
Considere el siguiente ejemplo donde necesitamos encontrar la corriente que fluye a través de una resistencia de 10 ohmios.
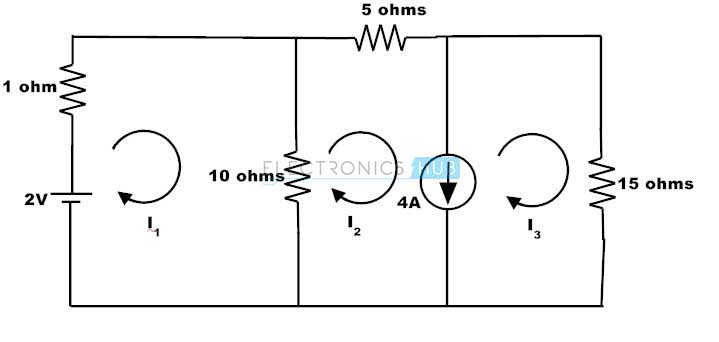
La aplicación de KVL a la malla 1 da como resultado:
1I1 + 10 (I1 – I2) = 2
11I1 – 10I2 = 2 ………………………. (1)
Las mallas 2 y 3 están compuestas por fuentes de corriente de 4 A y, por lo tanto, forman una súper malla. La corriente de la fuente de corriente de 4A está en la dirección de I3, por lo que la corriente de supermalla viene dada por:
Yo = I3 – I2
I3-I2 = 4…………………………. (2)
Aplicar KVL a los bucles exteriores de la supermalla resultante nos da
– 10 (I2 – I1) – 5I2 – 15I3 = 0
10I1 – 15I2 – 15I3 = 0…………………….. (3)
Resolver las ecuaciones 1, 2 y 3 nos da:
I1 = –2,35A
I2 = –2,78A
I3 = 1,22A
Por lo tanto, la corriente que fluye a través de la resistencia de 10 ohmios es I1 – I2.
= –2,35 + 2,78 A
= 0,43A
Volver a la cima