Tabla de contenido
Introducción
En la sección anterior, aprendimos sobre los sistemas numéricos decimales y binarios. En general, en los sistemas digitales, las expresiones y operaciones en cadenas largas son muy comunes. En un sistema numérico binario, los números binarios (cadenas largas) no pueden representar eficazmente más números. Es por eso que usamos otro sistema numérico llamado “sistema numérico hexadecimal” para representar fácilmente cadenas largas. Los sistemas numéricos decimales hexadecimales se utilizan ampliamente en la codificación del lenguaje ensamblador.
[adsense1]
Sistema decimal hexadecimal
En el término sistema numérico decimal hexadecimal, la palabra ‘hexa’ significa 16. Entonces, como su nombre indica, el sistema numérico decimal hexadecimal tiene 16 valores para la representación numérica, a saber, números del 0 al 9 y letras de la A a la F.
Hexa Decimal
Los números decimales hexadecimales se muestran en la siguiente tabla. Aquí, los 16 valores representan números del 0 al 15. Los números del 0 al 9 se muestran como de costumbre, pero los números del 10 al 15 se muestran con las letras de la A a la F. Los 16 números se utilizaron en varias combinaciones para representar números binarios y decimales.
A F le sigue de nuevo el número (10)16, que es igual a 16 en decimal, es decir, (1× (16))+ (0 ×(16)).
Cada decimal hexadecimal representa un grupo de 4 dígitos llamado “nibble”. En el sistema decimal hexadecimal, la posición de un número se pondera con una potencia de 16. En otras palabras, el valor numérico de la columna es 16 veces el valor numérico de la derecha.
Ejemplos: (10)16, (56)16, (3Fb1)16, (A51D0)16
Veamos algunos ejemplos más para entenderlo claramente
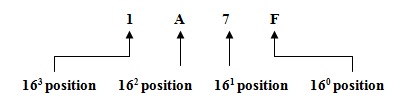
Este sistema decimal hexadecimal se utiliza para almacenar direcciones de datos en registros informáticos. Por ejemplo, si necesita proporcionar un gran número de cadenas binarias, 1011110110001011111010110001101 es muy difícil y causa mucha confusión. Por lo tanto, la computadora usa números decimales hexadecimales para representar estas cadenas.
Ir al principio
[adsense2]
Conversión decimal hexadecimal
Al convertir binario a decimal y decimal a binario, también puede convertir decimal hexadecimal a binario y sistema decimal.
Conversión de binario a decimal hexadecimal
Para convertir números binarios a decimales hexadecimales, agrupamos los números binarios en 4 conjuntos. Si es necesario, agregue ceros para completar el conjunto. Luego escribe ese número en cada grupo de números de 4 dígitos.
Ejemplo 1: Convertir (0110101110001100)2 a hexadecimal.
Dada 0110101110001100, agrupa los números binarios en un conjunto de números de 4 dígitos.
0110 1011 1000 1100
6 u 8 C
Por lo tanto, (0110101110001100)2 = (6B8C)16
Conversión de decimal hexadecimal a binario
Para convertir un número decimal hexadecimal en binario, siga los pasos inversos descritos anteriormente. Primero, escriba cada número en el número decimal hexadecimal en forma binaria y luego agrupe los números binarios.
Mirando algunos ejemplos que se dan a continuación, tendrá una idea clara de esto
Ejemplo 1: Convertir 5A9 a binario
5 Amperios 9
0101 1010 1001
Así que (5A9)16 = (10110101001)2
Conversión de decimal hexadecimal a decimal
Para convertir un decimal hexadecimal en un decimal, debe escribir cada número/letra en forma decimal con una base de 10 y luego escribir el decimal hexadecimal ha como la suma de potencias de 16.
Vea el ejemplo descrito.
Ejemplo 1: Convierta el número hexadecimal 1A9B a decimal.
1 A 9 B = 1 x 163 + A x 162 + 9 x 161 + B x 160 (capacidad de escritura de 16)
= 4096 + A (256) + 9 (16) + B (1)
= 4096 + 10 (256) + 144 + 11
= 6811
Por lo tanto, (1A9B)16 = (6811)10
Convertir de decimal a hexadecimal
Una forma sencilla de convertir decimales a decimales hexadecimalesEl sistema BER es el mismo que convertir un número decimal en un número binario. A partir de ahí, el proceso de división iterativa se realiza por 2, pero dado que el decimal hexadecimal es la base de 16, necesitamos hacer el proceso repetitivo de división por 2 en lugar de 16. Los recordatorios aparecen en el penúltimo orden.
Aprendamos esto con un ejemplo: Incluso
746 ÷ 16 Compartir 10, resto 46 resultados>A
46 ÷ 16 acciones 14, resto 2 resultados > E A
2 ÷ 16 acciones 0, resto 2 resultados> 2 e A
Por lo tanto, (746)10 = (2EA)16
Otro ejemplo: Impar
3509 ÷ 16 Compartir 219, restantes 5 resultados> 5
219 ÷ 16 Compartir 13, 11 resultados restantes> B 5
13÷ 16 share 0, restantes 13 resultados> D B 5
Así que (3509)10 = (DB5)16
Ir al principio
Representación numérica hexadémica
Hemos aprendido cómo convertir números decimales hexadecimales a otros sistemas numéricos y cómo convertir otros sistemas numéricos a decimales hexadecimales. Ahora, analicemos el cálculo de los números decimales hexadecimales.
Si necesita calcular más números hexadecimales que F, comience el cálculo de nuevo a partir de los números binarios. Esto se muestra a continuación.
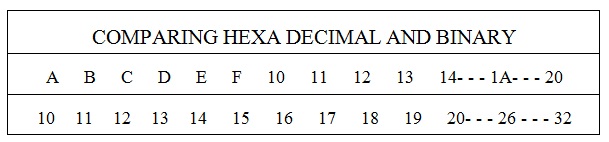
Memorándum:
Importante y esencial para recordar en el sistema decimal hexadecimal, si escribes (10)16 aquí, no es 10. 1×(16) + 0×(16) se representa como hexadecimal. Del mismo modo, si escribes 19 o 32 en hexadecimal, no es lo mismo que 19 o 32,1× (16) + 9× (16) y 3× (16) + 2× (16) en hexadecimal. simplemente
(10)10 no es lo mismo que (10)16.
(19)10 no es lo mismo que (19)16.
(32)10 no es igual a (32)16
En el sistema decimal, el número decimal positivo más alto es 255. En este sistema decimal hexadecimal, el número más alto formado con decimal hexadecimal es FF. Esto es igual a 255 en el sistema decimal y 1111 1111 en el sistema binario.
El número decimal hexadecimal mínimo de 3 bits es 10016 (25610) y el número más alto es FFF16 (409510). El número hexadecimal máximo de 4 dígitos es FFFF16 (65,53510).
Representación de números hexadecimales
Si tiene 4, 8, 12 o 16 números binarios, puede convertir fácilmente decimales y binarios a decimales hexadecimales agregando dígitos decimales hexadecimales
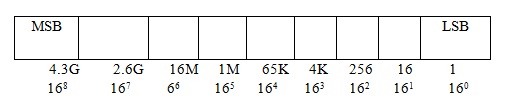
Por ejemplo, 10 1101 1000 1011 2 es un número binario de 14 dígitos, que es demasiado grande para representarse como un hexadecimal de 3 dígitos y demasiado pequeño para representarse como un hexadecimal de 4 dígitos. Entonces, para que la expresión sea cómoda, agregamos un cero a la izquierda del bit superior (MSB).
Entonces, la característica principal del sistema de numeración hexadecimal es que hay 16 números contables del 0 al F, y cada número tiene un peso (valor) de 16, comenzando desde el bit más bajo (LSB). Un prefijo se utiliza para distinguir los números hexadecimales de otros números. “#”, (almohadilla) o “$” (el signo de dólar antes del valor hexadecimal real)
Por ejemplo, #A5CE o $A 5CE.
Agregar 0 al binario
Notas decimales hexadecimalesLa ventaja es que es muy compacto para representar la dirección de un campo o datos en una computadora. Los números decimales hexadecimales tienen menos dígitos en comparación con los binarios. Se muestra a continuación.
Binario 0011 1110 0010 1011
Hexadecimal 3 E 2 B
Añade un cero a la izquierda del tiempo de nivel superior para que la expresión sea cómoda.
Ir al principio
Resumen de números hexadecimales
- La palabra “Hexa” significa 16. Como su nombre indica, el sistema decimal hexadecimal utiliza un conjunto de 16 dígitos. Son 0 – 9 y A – F.
- Los números decimales hexadecimales son utilizados principalmente por las computadoras para almacenar direcciones de datos.
- Estos números están representados por un signo ‘$’ (dólar) o un signo ‘#’ (almohadilla) delante de ellos. Por ejemplo, #A32C, $A 32C.
- El número decimal hexadecimal mínimo de 3 bits es 10016 (25610) y el número más alto es FFF16 (409510). El número hexadecimal máximo de 4 dígitos es FFFF16 (65,53510).
- En el siguiente capítulo, aprenderá sobre los esquemas numéricos octales y la decodificación de errores en diferentes tipos de sistemas numéricos.
Ir al principio