Tabla de contenido
- Introducción
- Representación de tamaño con signo
- Complemento de 1 de dígitos binarios con signo
- Adición de números binarios con signo
- Resta usando el elogio de 1
- Complemento de 2 de números binarios con signo
- Tabla que representa 1 y 2 complementos en decimales
- Resumen binario firmado
- Artículos relacionados:
Introducción
Por lo general, representa un número positivo (sin signo) sin signo y un número negativo con un signo “menos” (signo negativo) delante. Sin embargo, estos no se aplican a la computación de sistemas digitales como las computadoras, ya que los datos están representados por un sistema numérico binario. Por lo tanto, se requiere una notación especial para representar los símbolos.
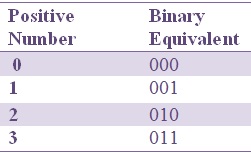
Números binarios con signo positivo
Los números binarios con un MSB de 0 se denominan “números binarios con signos positivos”.
Números binarios con signos negativos
Los números binarios con MSB 1 se denominan “binarios con signo negativo”.
Los números sin signo pueden tener una variedad de representaciones. Sin embargo, para los números con signo – (2(n-1) – 1) a + (2(n-1) – 1).
donde n es el número de bits (incluidos los bits de signo).
Batalla: Para un binario con signo de 5 bits (con 4 bits de tamaño y 1 bit con signo), el intervalo es el siguiente:
– (2(5-1) – 1) a + (2(5-1) – 1)
-(2(4) – 1 ) en + (2(4) – 1)
De -15 a +15
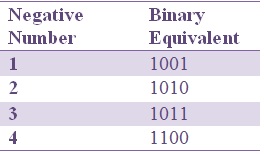
Los archivos binarios de 8 bits sin signo oscilan entre 0 y 255. Los archivos binarios firmados de 8 bits tienen un valor máximo y mínimo, como se muestra a continuación.
El número positivo máximo es 0111 1111 +127.
El número negativo máximo es 1000 0000 -127.
Ir al principio
Debido a que no podemos dar señales positivas o negativas a los sistemas digitales, necesitamos expresarlas de diferentes maneras. Hay tres formas comunes de representar números negativos dentro de una computadora. Son los siguientes:
- Representación de tamaño firmada.
- 1, expresiones complementarias.
- Expresión del complemento de 2.
Representación de tamaño con signo
Los números binarios, ya sean positivos o negativos, que pueden ser identificados por el bit de mayor significación (MSB) se denominan “binarios con signo”.
Batalla: 1001 — > + 9 (positivas) 1 001 — > – 1 (negativas)
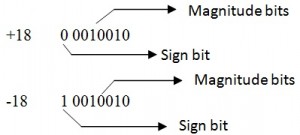
Esta es la forma más sencilla de representar números positivos y negativos en binario. En la expresión de tamaño con signo,
- Los números positivos se representan con ‘0’ en el bit más significativo (MSB).
- Los números negativos están representados por ‘1’ en el bit más significativo (MSB).
Ir al principio
Complemento de 1 de dígitos binarios con signo
El complemento de 1 es otra forma de alimentar a una computadora con un número binario negativo. En el método del complemento, el binario positivo no cambia. Sin embargo, un número negativo se expresa tomando el complemento de 1 de un número positivo sin signo.
Los números positivos siempre comienzan con 0 en MSB, y los números negativos siempre comienzan con 1 en MSB.
Se crea un complemento de 1 en un número reemplazando todos los ceros por 1 y todos los 1 por 0.
Por ejemplo, si el número binario es 01101001, entonces el complemento de 1 es 10010110.
Veamos algunos ejemplos más del complemento a 1.
Ejemplo 1: -33 =?
33 se denota con (100001).2
En notación de 8 bits, se denota como (0010 0001).2
-33 ahora se muestra como (1101, 1110) en alabanza2
Ejemplo 2: -127 =?
En notación de 8 bits, 127 está representado por (0111 1111).2
Ahora -127 se muestra como (1000 0000) en alabanza2
Ejemplo 3: -1 =?
1 está representado por (001).2
En notación de 8 bits, se denota como (0000 0001).2
Ahora -1 se muestra como (1111, 1110) en alabanza2
Complemento de 1 usando el inversor
La forma más sencilla de averiguar el complemento del número 1 requerido para un circuito electrónico digital es utilizar un “inversor”. Como su nombre indica, un verter es un dispositivo/circuito que genera cumplidos en la entrada.
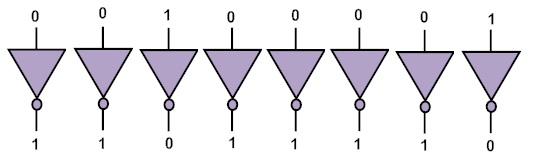
Los inversores se conectan en paralelo para compensar el 1 del binario de entrada. No importa cuántos dígitos tenga un número binario, puedes encontrar fácilmente el complemento binario. Con solo escribir todos los ceros como 1 y 1 como 0, 1 puede complementar el binario.
Las operaciones matemáticas que se realizan sobre números binarios se denominan “aritmética binaria”. Puedes sumar o restar números positivos o negativos de varias maneras, como A+B, A+(-B), -B+A, etc.
Ir al principio
Adición de números binarios con signo
La suma binaria sigue las mismas reglas que la suma regular. Sin embargo, la única excepción aquí es que la operación matemática solo se realiza entre dos dígitos (0 y 1). Siempre es 1>0.
Reglas para la suma binaria
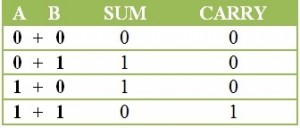
Ir al principio
Resta usando el elogio de 1
Si quieres restar un número de otro número binario, primero debes convertirlo en tu propio complemento.
Hay 3 casos en los que se utiliza un cumplido de 1 para restar un número negativo.
Caso 1 : un número negativo menor que un número positivo.
Batalla: (28)10 & (-15)10
Sabemos que 28 está representado por (011100) en un sistema numérico binario.2
15 está representado por (01111) en el sistema numérico binario.2
1, Alabanza 15 (10000)2 es decir, -15
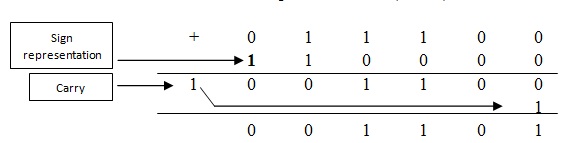
(13)10 es igual a 0 01101 en binario.
Caso 2: Un número negativo mayor que un número positivo.
Batalla: (-28)10 & (15)10
Sabemos que 28 está representado por (011100) en un sistema numérico binario.2
15 está representado por (01111) en el sistema numérico binario.2
1 en alabanza de 28 (100011)2 es decir, -28
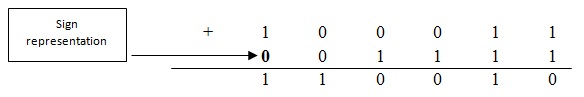
(-13)10 Es igual a 1 10010 en binario.
Caso 3: Ambos son negativos.
Batalla: (-28)10 & (-15)10
Sabemos que 28 está representado por (011100) en un sistema numérico binario.2
1 en alabanza de 28 (100011)2es decir, -28
15 está representado por (01111) en el sistema numérico binario.2
1, Alabanza 15 (10000)2 es decir, -15
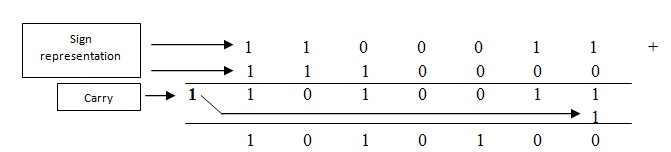
(-43)10 Es equivalente a 1010100 en binario.
Ir al principio
Complemento de 2 de números binarios con signo
El proceso de encontrar es similar al proceso de calcular 10 en decimal. Para encontrar un cumplido de 2 para un número binario, primero debes encontrar el cumplido de 1 para ese número y luego agregar “1” al elogio de 1 más tarde.
La representación complementaria de 2 para un número positivo es la misma que la representación de la alabanza y la representación de magnitud firmada de 1.
Encontrar los cumplidos de 2 implica los dos pasos que se describen a continuación.
Paso 1: Buscar cumplidos
Paso 2: Agregue ‘1’ al resultado de un número sin signo.
Entendamos esto con algunos ejemplos.
Ejemplo 1: -33 =?
33 se denota con (100001).2
En notación de 8 bits, se denota como (0010 0001).2
-33 ahora se muestra como (1101, 1110) en alabanza2
Agregue 1 (0000 0001) a esto,
El resultado es (1101 1111).2
Así, los dos complementos del número 33 son (1101 1111)2.
Ejemplo 2: -127 =?
En notación de 8 bits, 127 está representado por (0111 1111).2
Ahora -127 se muestra como (1000 0000) en alabanza2
Agregue 1 (0000 0001) a esto,
El resultado es (1000,0001).2
Así, los dos complementos del número -127 son (1000 0001)2
Ejemplo 3: -1 =?
1 está representado por (001).2
En notación de 8 bits, se denota como (0000 0001).2
-1 ahora está representado por (1111, 1110)2 en alabanza
1 más (0000 0001) a él,
El resultado es (0000 0010).2
Por lo tanto, los dos complementos del número -1 son (0000 0010)2
Ir al principio
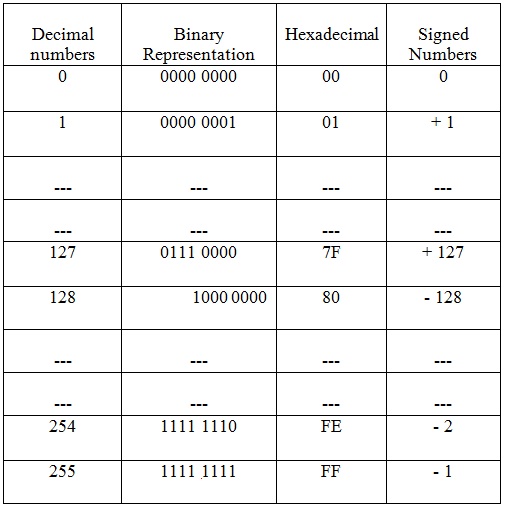
Tabla que representa 1 y 2 complementos en decimales
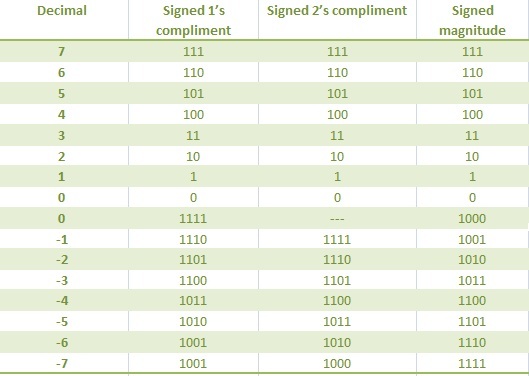
Ir al principio
Resumen binario firmado
Los números binarios que pueden ser identificados por los MSB se denominan “binarios con signo”.
Si MSB es 1, es un “binario con signo negativo”. Batalla: – 1 = 1001 años
Si el MSB es 0, es un “binario con signos positivos”. Batalla: + 9 = 1001 años
Las computadoras no pueden entender el signo menos. Por lo tanto, si desea dar un número negativo como entrada, seguirá 3 métodos especiales: Son los siguientes:
1) Representación de tamaño firmada
2) 1, Expresiones elogiosas
3) 2, expresión de elogio
Un cumplido de 1 significa “reemplace todos los 1 con 0 y los 0 con 1”.
Batalla: Elogio 1 de 15, es decir, 15 es (10000).2 es decir, -15
Un elogio de 2 significa “sumar 1 al elogio de 1 del número requerido”.
Batalla: El número – 33 es un complemento de 2 is (1101 1111).2.
Las operaciones matemáticas, como la suma y resta de números binarios, se denominan “operaciones aritméticas binarias”.
Ir al principio