En este tutorial, aprenderá sobre el código binario de un sistema numérico binario, que es uno de los requisitos básicos de la electrónica digital. Algunos de los códigos binarios más populares son BCD (8421), 2421, 5211, Excess-3, Gray.
Tabla de contenido
Introducción
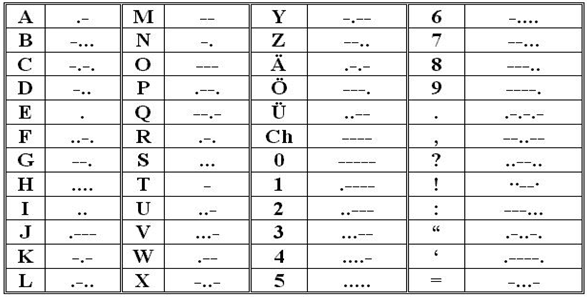
El primer sistema de telecomunicaciones exitoso fue el telégrafo, inventado por Samuel F.B. Morse en 1832. El operador de telégrafo utilizó un código de clic para enviar el mensaje. La pulsación corta de la tecla es el código Morse para ‘punto’ y la pulsación larga para ‘guión’. A continuación, se muestra un ejemplo de código Morse:
Lógicamente, puede usar el código anterior para escribir varias combinaciones de puntos y rayas en todo tipo de palabras (incluidas oraciones). De la misma manera, los números binarios también se utilizan para crear estas diversas combinaciones de miríadas. Esto se puede considerar código binario.
Además del código 8421 o el código BCD de uso común, también se utilizan ampliamente otros códigos binarios como el código 2421, el código 5211, el código de reflexión, el código secuencial, el código no ponderado, el código de más de 3 y el código gris.
Código binario de uso común
Antes de sumergirnos en los códigos binarios individuales, echemos un vistazo rápido a algunos de los códigos binarios más utilizados. Aquí está la lista:
- Código 8421
- Código 2421
- Código 5211
- Exceso – 3 código
- Código gris
Los tres primeros de la lista anterior, a saber, 8421, 2421 y 5211, son códigos binarios ponderados, mientras que los otros dos son códigos binarios no ponderados.
Sistema binario ponderado
En el sistema decimal, que es un sistema de dígitos, los valores asignados a dígitos consecutivos son 10⁴, 10³, 10², 10¹, 10⁰, 10⁻¹, 10⁻², 10⁻³… Continúa de izquierda a derecha. Es fácil entender que el peso de los dígitos decimales es ’10’.
Por ejemplo:
(3546.25)10 = 3 x 10³ + 5 x 10² + 4 x 10¹ + 6 x 10⁰ + 2 x 10⁻¹ + 5 x 10⁻²
De la misma manera, en binario, que también es un sistema de valor posicional, los valores asignados a lugares contiguos se denominan binarios ponderados.
Los pesos en binario son 2⁴, 2³, 2², 2¹, 2⁰, 2⁻¹, 2⁻², 2⁻³… De izquierda a derecha. Es fácil entender que el peso de un dígito en binario es ‘2’.
Por ejemplo:
(1110110)2 = 1 x 2⁶+ 1 x 2⁵ + 1 x 2⁴ + 0 x 2³ + 1 x 2² + 1 x 2¹ + 0 x 2⁰
= 64 + 32 + 16 + 0 + 4 + 2 + 0 = (118)10
Pesos binarios
Cada vez que aparece un número binario, puede encontrar fácilmente el equivalente de un número decimal como este:
- Si hay un 1 en la posición del dígito, debe agregar el peso de esa posición.
- Si hay un cero en la posición numérica, se debe ignorar el peso en esa posición.
Por ejemplo, el número binario 1100 tiene un número decimal que corresponde a 8 + 4 + 0 + 0 = 12.
Código 8421 o código BCD
Los números decimales 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 se pueden expresar en binario como se muestra en la tabla siguiente. Todos estos binarios se expanden a 4 bits y se reexpresan en la última columna. Dependiendo del binario ponderado, el binario de 4 bits se puede expresar como 8421 (2³ 2² 2¹ 2⁰ = 8421) dependiendo del valor posicional de izquierda a derecha.
De acuerdo con la expresión anterior, todos los números decimales escritos en código binario de 4 bits son códigos 8421, también conocidos como BCD decimales de código binario.
Este es un código recto, por lo que puede representar fácilmente el número CIMAL porque los pesos en la posición son rectos, de modo que todos los De se pueden convertir fácilmente en códigos 8421.
Hay otras formas de código que no son muy populares, pero algo confusas. Estos son códigos 2421, códigos 5211, códigos reflexivos, códigos secuenciales, códigos no ponderados, códigos de más de 3 y códigos grises. Tienen su propio significado para algunas de las aplicaciones exclusivas y pueden ser útiles para algunas aplicaciones especiales.
Código 2421
Este código también es código de aplicación de 4 bits, con pesos binarios que pasan 2, 4, 2, 1 de izquierda a derecha.
Código 5211
Este código también es código de aplicación de 4 bits, con pesos binarios que pasan 5, 2, 1, 1 de izquierda a derecha.
Código reflectante
En los códigos 2421 y 5211, el código del decimal 9 es el complemento del código del decimal 0, el código del decimal 8 es el complemento del código del decimal 1 y el código del decimal 7 es Puede ver que el código es el complemento del código para el decimal 2, y el código para el decimal 6 es el complemento del código para el decimal 3. El código para el decimal 5 complementa el código para el decimal 4. Estos códigos se denominan códigos de reflexión. Puede ver lo mismo en la siguiente tabla.
Memorándum: El código 8421 no es un código de reflexión.
Códigos secuenciales
Un código secuencial es aquel en el que dos números posteriores en una representación binaria difieren solo un dígito. Los códigos 8421 y Excess-3 son ejemplos de códigos secuenciales. Los códigos 2421 y 5211 no pertenecen a los códigos secuenciales.
Código no ponderado
Algunos códigos no respetan los pesos de los binarios de secuencia, lo que se denomina código no ponderado. Los códigos ASCII y los códigos grises son algunos ejemplos que se codifican para algunas aplicaciones de propósito especial y no siguen cálculos binarios ponderados.
Exceso – 3 código
Como se mencionó anteriormente, algunos códigos no siguen pesos binarios, y el código Excess-3 es un ejemplo de esto, y es un código importante de 4 bits. Exceso de decimales: se logran 3 acordes sumando n. Del umber 3 al código 8421.
Por ejemplo, si desea convertir 15 en un código de exceso de 3, agregue los primeros 3 a cada número como se muestra a continuación.
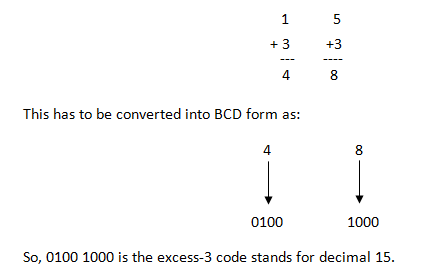
Exceso – 3 ejemplos de código
- Buscar código excess-237.75 en (3)10
- excess-3 encuentra el dígito decimal del número 110010100011.0111010101.
Cepillo:
1) Código de exceso para 237-310 Se obtiene sumando 3 a todos los números individualmente, es decir, 2, 3 y 7 se convierten en 5, 6 y 10, respectivamente. Estos números primos 5, 6 y 10 deben convertirse a forma binaria, y el resultado es 010101101010.
Código de exceso-3 para (.75)10 Lo obtienes sumando 7 a cada número reemplazando 5 y 10 con 8 y 3 respectivamente. En otras palabras, es un código de exceso de 3 para (.75).10 es .10101000.
Combinando los resultados de las partes integral y fraccionaria obtenemos el código sobre 3 para (237.75)10 010101101010.10101000.
2) El código Beyond -3 es 110010100011.01110101.
Si separamos los 4 bits en grupos, el código equivalente en exceso de 3 es 1100 1010 0011.0111 0101.
Si resta 0011 de cada grupo de 4 bits, el nuevo número es 1001 0111 0000.0100 0010.
Por lo tanto, el número decimal es (970.42)10.
Código gris
Un código gris es un código en el que 1 bit es diferente del número anterior. Por ejemplo, los números decimales 13 y 14 están representados por los números de código gris 1011 y 1001, que difieren solo en una posición, la segunda posición desde la derecha. De la misma manera, la primera posición de la izquierda cambia para 7 y 8 (0100 y 1100), que también se conoce como código de distancia unitaria. El código gris ocupa un lugar muy especial en la electrónica digital.
conclusión
Este es un tutorial introductorio sobre código binario. Aprendí varios códigos binarios como BCD (8421), 2421, 5211, Excess-3 y Gray Codes.