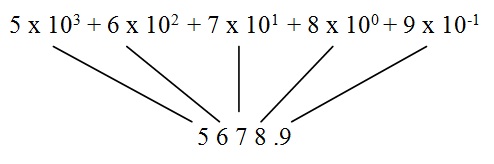La representación de los números se denomina “sistema numérico” o “sistema numérico”. Desde el punto de vista de los electrones digitales, existen diferentes tipos de sistemas numéricos como ‘binario’, ‘octal’, ‘hexadecimal’, ‘decimal’, etc.
Tabla de contenido
Sistema decimal
Este es el sistema numérico que utilizamos en nuestra vida diaria. El sistema considera que la posición numérica de un número son unidades, decenas, centenas, miles, etc. La posición del número en relación con el separador decimal determina su valor. La base del número decimal es 10. Calculemos los números en forma decimal de la siguiente manera:
Batalla:
848: ochocientos cuarenta y ocho. +8:800 + 40
8 centenares = 8 x 100 = 8 x 102
4 decenas = 4 x 10 = 4 x 101
8 unidades = 8 x 1 = 8 x 100
Ahora 8 x 102 + 4 x 101 + 8 x 100 = 848
donde el bit más a la izquierda se denomina “bit de nivel superior” o “VELOZy el bit más a la derecha se denomina “bit más bajo” o “LSB”.
Veamos otro ejemplo.
5678.9:5000 + 600 + 70 + 8 + 0.9
A partir de la potencia de 10, podemos escribir el número anterior de la siguiente manera:
5 x 103 + 6 x 102 + 7 x 101 + 8 x 100 + 9 x 10-1
5 6 7 8 .9
Ir al principio
Sistema Numérico Binario
El sistema numérico binario utiliza solo los números de dos dígitos 0 y 1. Es un sistema de numeración posicional, lo que significa que las posiciones se ponderan a la potencia de dos. La mayoría de las veces, los sistemas binarios se utilizan en sistemas digitales. Los datos de la computadora deben estar en formato binario 0 y 1.
Ejemplos para entender el sistema numérico binario
21 se expresa como 10101 en binario.2 = 1 × 24 + 0 × 23 + 1 × 22 + 0 ×21 + 1 ×20 = 16 + 4 + 1 = 21
23 se expresa como 10111 en binario.2 = 1 × 24 + 0 × 23 + 1 × 22 + 1 × 21 + 1 × 20 = 16 + 4 + 2 + 1 = 23
35 se expresa en binario de la siguiente manera 1000112 = 1 × 25 + 0 × 24 + 0 × 23 + 0 × 22 + 1 × 21 + 1 × 20 = 32 + 2 + 1 = 35
0 o 1 es ‘Golpea’.‘picar‘ es una combinación de 4 bits. ‘byte‘ es una combinación de 8 bits. Normalmente vamos a medir el tamaño de la memoria. byte.
Ir al principio
Conversión de binario a decimal
Puede convertir binario a decimal de 2 maneras. Son los siguientes:
1. Multiplique cada número binario por el valor de la posición.
Contando desde la derecha, el valor del bit más a la derecha es 1, el valor del siguiente bit es 2, el valor del siguiente bit es 4, el valor del siguiente bit es 8, y así sucesivamente.
Por ejemplo, convierta 1011 en un decimal
cepillo
8 x 1 + 4 x 0 + 2 x 1 + 1 x 1 = (11)10
(8) (0) (2) (1)
Ir al principio
Repetir la división por 2.2
Una forma conocida y fácil de convertir un número decimal en binario es la “división iterativa 2”.
Cómo convertir un número entero de una base a otra es “División repetida“. Si divides el número decimal por el número base, obtienes el cociente de “R”.Eminder“. La notificación se escribe en el primer binario y el cociente se divide de nuevo por el número base, por lo que se obtiene el segundo cociente y la segunda notificación. Esto se registra como el segundo dígito binario y este proceso continúa hasta que el cociente llega a cero.
De esta forma, si divides el número decimal entre 2, la notificación solo será 0 o 1. El resultado binario se obtiene escribiendo la primera notificación como el ‘bit más bajo’ y la última como el ‘bit más significativo’.
Intentemos con un ejemplo. número cardinal
43 ÷ 2 Compartir 21, resultado restante 1 > 1
21 ÷ 2 Cuota 10, resto 1 Resultado > 1 1
10 ÷ 2 Cuota 5, resto 0 Resultado > 0 1 1
5 ÷ 2 Cuota 2, resto 1 Resultado > 1 0 1 1
2 ÷ 2 Compartir 1, Resto 0 Resultado > 0 1 0 1 1
1 ÷ 2 Cuota 0, resto 1 Resultado> 1 0 1 0 1 1
número par
36 ÷ 2 Compartir 18, resto 0 Resultado > 0
18 ÷ 2 Cuota 9, resto 0 Resultado> 0 0
9 ÷ 2 Cuota 4, resto 1 Resultado> 1 0 0
4 ÷ 2 Cuota 2, Resto 0 Resultado > 0 1 0 0
2 ÷ 2 Compartir 1, resto 0 Resultados > 0 0 1 0 0
1 ÷ 2 cuota 0, resto 1 resultado > 1 0 0 1 0 0
Otro ejemplo
Descapotables 9310 Binario
93 / 2 = 46 resto 1 (dígito más bajo)
46 / 2 = 23 restantes 0
23 / 2 = 11 resto 1
11 / 2 = 5 resto 1
5 / 2 = Resto 2 1
2 / 2 = resto 1 0
1 / 2 = 0 resto 1 (dígito superior)
Representación binaria de (93)10 1 0 1 1 1 0 1.
Si dividimos aun Si reemplaza el número decimal por 2, la notificación se mostrará como 0. Si divides un número decimal impar, la notificación aparecerá como 1.
El resultado binario de los números decimales se puede obtener ordenando la primera notificación en el MSB y la última notificación en el LSB.
Ir al principio
Representación de números binarios
Ya sabemos que el sistema decimal está representado por el número de base 10, lo que significa que el peso de cada número (empezando por la izquierda) aumenta en un factor de 10. Del mismo modo, todos los números binarios están representados por una base de 2, por lo que el peso de cada número (empezando por la izquierda) se duplica (por ejemplo, el primer dígito está representado por 2).0 Segundo número al 21 Etcétera.
Como aprendimos en el sistema numérico binario en la sesión anterior, la menor potencia posible de 2 es 20 El valor más alto es 2.8 (en un sistema binario de 8 bits).
Para entender esto claramente, vea la imagen a continuación.
Ir al principio
Nombres binarios y prefijos
Nombre numérico
Los números binarios también realizan operaciones matemáticas como la suma y la resta. Por lo tanto, en la suma y la resta, los números decimales están representados por grupos binarios (0 y 1). Básicamente, se conocen tres tipos de grupos binarios: Bit, Byte, Word.
0 o 1′bit‘
4 bits son ‘picar‘
8 bits o 2 mordiscos es ‘byte‘
16 bits, o 4 nibbles, o 2 bytes es ‘Palabra’
32 bits u 8 nibbles o 4 bytes o 2 palabras’Doble’
64 bits o 16 nibbles o 8 bytes o 4 palabras o 2 dobles’Cuádruple’
Prefijo numérico
al convertir datos/información de un sistema digital de una notación a otra, es decir, de binario a decimal y de decimal a binario; Debido a que los datos pueden variar de una notación a otra, solo se debe seguir una de las dos notaciones. Por ejemplo, si dices “10”, puedes expresarlo como “10” en decimal y en notación binaria podría verse como “1” y “0” (como el número 2).
Puede superar este problema escribiendo un subíndice al final de un número o número. Este subíndice se denomina “prefijo”. Por ejemplo, si representas un número en binario, debes expresarlo como (1101011).2 & Para el sistema numérico decimal (432)10 & – Representación del sistema decimal hexadecimal (480)Hexadecimal.
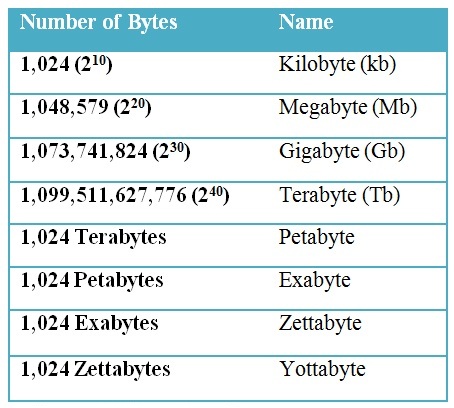
Ahora, el mundo electrónico digital se está desarrollando rápidamente y la representación de números tiene una nueva forma. Son un poco (pequeño) a Yotabyte (Máximo).
Ir al principio
Resumen
Normalmente, los terabytes se utilizan como el tamaño de memoria más grande.
- La palabra “Dígito binario” se llama “BIT”.
- El sistema decimal es algo que usamos para representar números de forma regular.
- En el sistema decimal, los números están representados por la base 10. Ejemplo: (432)10
- En un sistema numérico binario, o sistema numérico binario, solo hay dos dígitos (0 y 1).
- Los números binarios se ponderan de izquierda a derecha a potencias de dos.
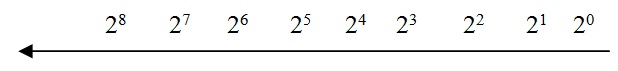
- Hay dos formas de convertir un número decimal en binario.
- Método de suma ponderada.
- Repite la división por 2.
- Al convertir un número de binario a decimal o de decimal a binario, se sigue la notación de prefijo para que no haya errores en la comprensión del tipo de sistema numérico que representa el número.
- Los números binarios tienen muchos nombres, como Bit, Nibble, Byte, Word, etc. Los bits son los más pequeños y los terabytes son los más altos.
En tutoriales posteriores, estudiaremos los sistemas numéricos octales y hexadecimales y sus conversiones.
Ir al principio