Resistencias paralelas

Introducción

Si ambos terminales de una resistencia están conectados a los respectivos terminales de la otra resistencia, entonces se dice que las dos resistencias están conectadas en paralelo. En una red de resistencias paralelas, a diferencia de una red de resistencias en serie, hay múltiples caminos a través de los cuales fluye la corriente, por lo que la corriente puede seguir múltiples caminos. Por lo tanto, el circuito de resistencia en paralelo es un divisor de voltaje.

Resistencias paralelas

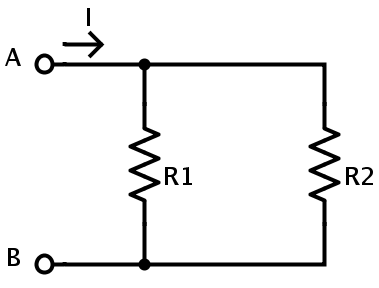
Cuando dos o más resistencias están conectadas en paralelo, la diferencia de potencial entre cada resistencia es la misma. Las resistencias conectadas en paralelo están conectadas al mismo nodo. Esto se puede identificar por los múltiples caminos a través de los cuales fluye la corriente. Por ejemplo, el circuito que se muestra a continuación es una conexión en paralelo de resistencias. La diferencia de potencial a través de la resistencia R1 es la misma que la diferencia de potencial a través de la resistencia R2 y es igual al potencial de la fuente de alimentación V_{Grupo sanguíneo}.

Si V_{Grupo sanguíneo} es el potencial que se suministrará en ese momento.

V_R1 =V_R2 =V_{Grupo sanguíneo}

En el siguiente circuito, las resistencias R1, R2 y R3 están conectadas en paralelo.

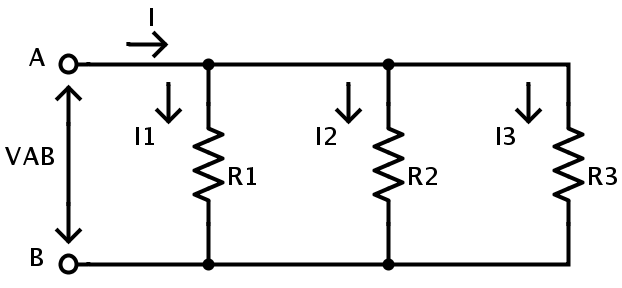
donde el potencial de potencia es V_{Grupo sanguíneo} Entre el punto A y el punto B. Dado que las resistencias R1, R2 y R3 están conectadas en paralelo, la diferencia de potencial entre cada resistencia es la misma que la de la fuente de alimentación. Por lo tanto, V_{Grupo sanguíneo} =V_R1 =V_R2 =V_R3.

Dónde

V_R1 es el potencial a través de la resistencia R1.

V_R2 es el potencial a través de la resistencia R2.

V_R3 es el potencial a través de la resistencia R3.

Sin embargo, la corriente que fluye a través de estas tres resistencias es diferente. Si I es el nodo de salida actual A, entonces hay tres caminos para llegar al nodo B. La corriente que fluye a través de cada resistencia depende de su resistencia. Por lo tanto, en el caso de los circuitos de resistencias en paralelo, la corriente no es la misma para todas las resistencias. Si I1 es la corriente que fluye a través de la resistencia R1, I2 es la corriente que fluye a través de la resistencia R2 e I3 es la corriente que fluye a través de la resistencia R3, entonces las corrientes I, I1, I2 e I3 se pueden relacionar con la ayuda de la ley de corriente de Kirchhoff. De acuerdo con la ley de las corrientes de Kirchhoff, “la suma de las corrientes que entran en el nodo es igual a la suma de las corrientes que salen del nodo”.

por consiguiente

I = I1 + I2 + I3.

Resistencia equivalente

Cualquier número de resistencias conectadas en paralelo puede ser reemplazado por una resistencia con una resistencia igual a la resistencia equivalente de la resistencia combinada en paralelo.

Se ha establecido que el voltaje a través de cada resistencia en una combinación en paralelo es el mismo, y la corriente total es igual a la suma de las corrientes individuales. Considere el siguiente circuito:

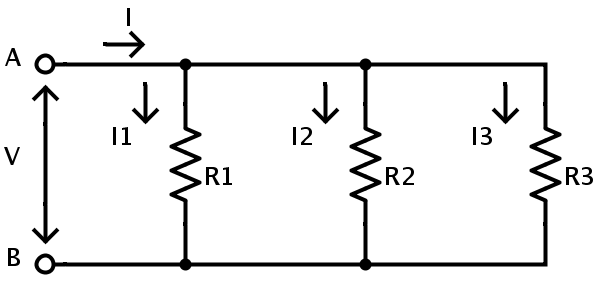
donde I = I1 + I2 + I3

I1 = V / R1

I2 = V / R2

I3 = V / R3

Si R_T es la resistencia total del circuito.

I = V/R_T

Por lo tanto, V/R es_T =V / R₁ + V / R₂ + V / R₃

1/R_T = 1 / R₁ +1/R₂ +1/R₃

Si R_EQ es la resistencia equivalente del circuito, que se calcula sumando el recíproco (1/R) de las resistencias individuales. El recíproco de esta suma algebraica da una resistencia igual. Ecuación para la resistencia equivalente R_EQ A continuación se muestra el circuito de resistencia en paralelo de n resistencias.

(1/R_EQ) = (1/R1) + (1/R2) + (1/R3) + ……… + (1/Rn)

A partir de la ecuación anterior, se puede ver que la resistencia equivalente de las resistencias conectadas en paralelo es siempre menor que el valor de resistencia de la resistencia más pequeña.

Si dos resistencias están en paralelo, la resistencia equivalente es:

(1/R_EQ) = (1/R1) + (1/R2)

R_Iko =R₁ * R₁ / (R₁ + Tecla R₂)

Si dos resistencias de igual resistencia R se combinan y conectan en paralelo, la resistencia equivalente de la combinación será R / 2.

Del mismo modo, si combinas y conectas tres resistencias de igual resistencia R en paralelo, la resistencia equivalente de la combinación será R/3.

Cuando las resistencias se conectan en paralelo, se obtiene el valor de conductancia. La conductancia es el recíproco de la resistencia. Generalmente se representa con el símbolo G. La unidad de conductancia es Siemens, denotada por el símbolo S, y anteriormente la unidad de conductancia era Mho (א), que es la ortografía inversa de Ohm, y el símbolo es una representación invertida de Ω.

Incluso si las resistencias paralelas están conectadas entre dos nodos, la representación de esta conexión puede ser de una de las siguientes formas:

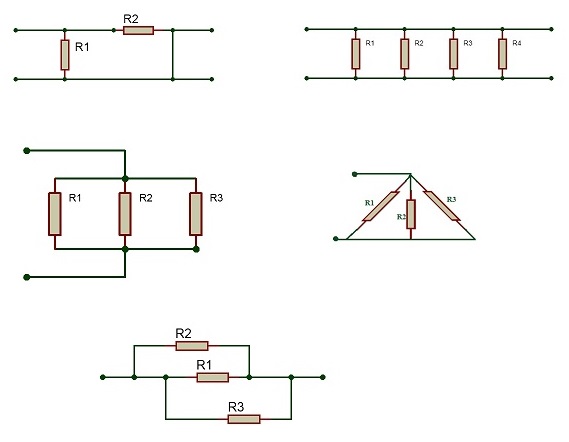
Todas las combinaciones anteriores son circuitos resistivos paralelos, y todas las reglas de las resistencias paralelas también se pueden aplicar a las combinaciones anteriores.

Cálculos actuales

La corriente en cada rama del circuito de resistencia en paralelo es diferente de las demás. Dado que el voltaje a través de cada resistencia es el mismo, la corriente que fluye a través de cada resistencia depende del valor de resistencia de esa resistencia. Por lo tanto, si el valor de resistencia de una rama es diferente de las demás, entonces la corriente en esas ramas será diferente. El valor de su corriente se puede determinar usando la ley de Ohm.

Considere una red paralela de dos resistencias con un voltaje de alimentación V entre dos puntos A y B.

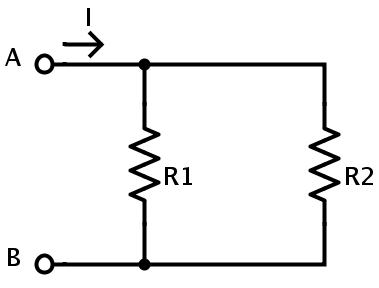
Sea I la corriente total en el siguiente circuito.

Aplicación de una corriente a la resistencia R₁ B.I._R1 Corriente que fluye a través de la resistencia R₂ B.I._R2.

De acuerdo con la ley de corriente de Kirchhoff, “la corriente total que entra en el circuito es igual a la corriente que sale del circuito”.

Si yo_T es la corriente total.

Yo_T = I_R1 Tecla + I_R2

Debido a que la caída de voltaje a través de cada resistencia es la misma

Yo_R1 =V / R₁

Y yo estoy_R2 =V / R₂

Considerando un circuito de resistencia en paralelo que consta de n resistencias, la corriente total en el circuito es:

Yo_total = I_R1 Tecla + I_R2 +…. + I_Rn

Si un circuito resistivo en serie se denomina circuito divisor de voltaje, de manera similar, un circuito resistivo paralelo se denomina circuito divisor de corriente.

Considerando un circuito de resistencia en paralelo de n resistencias con diferentes resistencias, podemos tener n caminos diferentes para que fluya la corriente y n valores diferentes de corriente a través de ese camino. Las resistencias combinadas en paralelo se pueden reemplazar sin afectar la corriente total y la resistencia equivalente.

Ejemplo de resistencias paralelas

1. Considere el siguiente circuito en el que cuatro resistencias R1, R2, R3 y R4 están conectadas en paralelo.

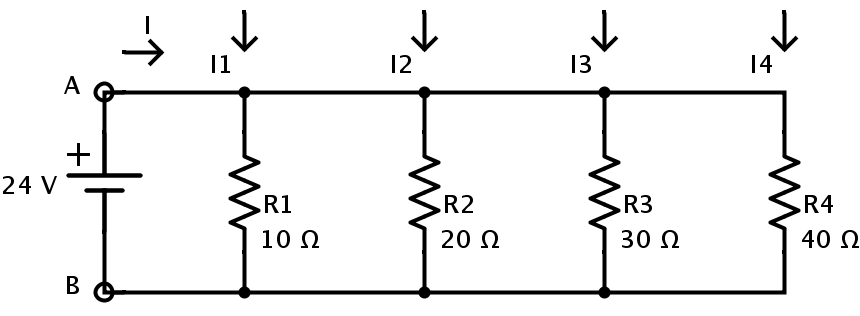
El valor de resistencia de cada resistencia viene dado por la siguiente ecuación:

R1 = 10 Ω

R2 = 20 Ω

R3 = 30 Ω

R4 = 40 Ω

La tensión de alimentación es V = 24 V

La corriente total en el circuito se puede calcular de dos maneras:

El primer método consiste en calcular las corrientes individuales que fluyen a través de cada resistencia.

Si I1 es la corriente que fluye a través de la resistencia R1, entonces de acuerdo con la ley de Ohm

I1 = V/R₁ = 24/10 = 2,4 A

De manera similar, si I2 es la corriente que fluye a través de la resistencia R2, entonces de acuerdo con la ley de Ohm

I2 = V/R₂ = 24/20 = 1,2 A

Si I3 es la corriente que fluye a través de la resistencia R3, entonces de acuerdo con la ley de Ohm

I3 = V/R₃ = 24/30 = 0,8 A

Y si I4 es la corriente que fluye a través de la resistencia R4, entonces de acuerdo con la ley de Ohm

I4 = V/R₄ = 24/40 = 0,6 A

Si yo_total es la corriente total en el circuito, y de acuerdo con la ley de corriente de Kirchhoff,

Yo_total = I1 + I2 + I3 + I4 = 2,4 + 1,2 + 0,8 + 0,6 = 5A

La segunda forma de calcular la corriente es encontrar la resistencia equivalente del circuito.

La resistencia equivalente del circuito viene dada por:

1/R_Iko = (1/ R₁) + (1/R₂) + (1/ R₃) + (1/R₄)

1/R_Iko = (1/10) + (1/20) + (1/30) + (1/40)

R_Iko = 1/2.083 = 4.8 Ω

Esta resistencia única se puede utilizar para reemplazar todas las resistencias en combinaciones en paralelo.

∴ yo_total = V/R_Iko = 24/4,8 = 5A.

Considere el siguiente circuito en el que tres resistencias R1, R2 y R3 están conectadas en paralelo.

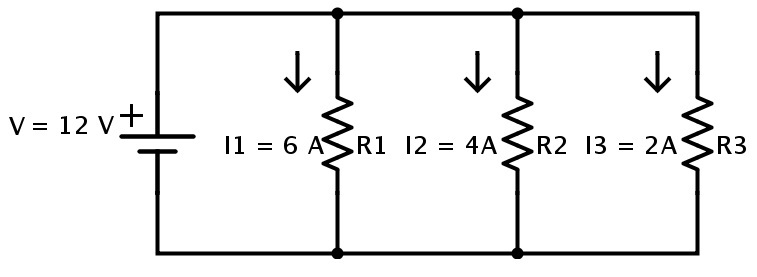
La corriente que fluye a través de R1 es I1 = 6A

La corriente que fluye a través de R2 es I2 = 4A

La corriente que fluye a través de R3 es I3 = 2A

En un circuito de resistencia en paralelo, el voltaje a través de cada resistencia es el mismo e igual al voltaje de alimentación.

donde la tensión de alimentación es V = 12 V.

Si V1 es el voltaje a través de la resistencia R1, V2 es el voltaje a través de la resistencia R2 y V3 es el voltaje a través de la resistencia R3, entonces

V = V1 = V2 = V3 = 12V

Entonces, de acuerdo con la ley de Ohm

R1 = V₁ /Yo₁

R1 = 12 / 6

R1 = 2 Ω

R2 = V₂ /Yo₂

R2 = 12/4

R2 = 3 Ω

R3 = V₃ /Yo₃

R3 = 12/2

R3 = 6 Ω

aplicación

El concepto de resistencia paralela se utiliza para analizar los circuitos de los puentes de Wheatstone. Las resistencias combinadas en paralelo actúan como un circuito divisor de flujo. Este concepto de divisor de voltaje se utiliza completamente en aplicaciones como convertidores de analógico a digital y convertidores de digital a analógico.