En el tutorial anterior, vimos los filtros pasivos, es decir, ambos. Filtros RC pasivos de paso alto Y Filtros RC pasivos de paso bajoEn este tutorial, aprenderá sobre los filtros activos, especialmente los filtros activos de paso alto.
Como su nombre indica, un filtro de paso alto solo permite el componente de alta frecuencia de la señal y limita el componente de baja frecuencia. La parte activa del nombre indica que en el diseño del filtro se utilizan componentes activos como transistores, amplificadores operacionales, etc.
Si buscas información sobre los filtros de paso bajo activos, consulta este tutorial. Filtro de paso bajo activo.
Tabla de contenido
- Introducción
- Filtro electrónico activo de paso alto
- Filtro activo de paso alto con alta ganancia de voltaje
- Ganancia de voltaje del filtro de paso alto activo
- Respuesta en frecuencia del filtro de paso alto activo
- Filtro de paso alto activo mediante un amplificador operacional inversor
- Derivación de ganancia en la forma de Laplace.
- Ejemplo de un filtro de paso alto activo
- Trama de Bode
- Filtro de paso alto de segundo orden
- Filtro de paso alto de alto orden
- Aplicaciones de los filtros activos de paso alto
- Artículos Relacionados:
Introducción
El filtro de paso alto permite frecuencias superiores a la frecuencia de corte y atenúa las frecuencias por debajo de la frecuencia de corte. En algunos casos, este filtro también se conoce como filtro de “corte bajo” o “corte base”. El rango de atenuación o banda de paso depende de los parámetros de diseño del filtro.
La ganancia de banda de paso del filtro activo es mayor o igual que la ganancia unitaria. Un filtro activo de paso alto se comporta igual que un filtro pasivo de paso alto, pero la principal diferencia es que un filtro activo de paso alto utiliza un amplificador operacional que proporciona amplificación de la señal de salida y control de la ganancia.
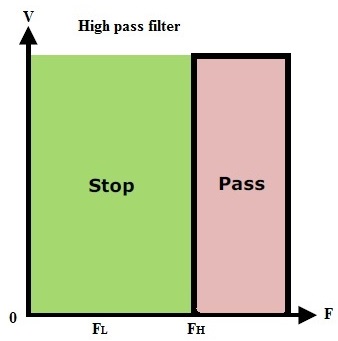
A continuación se muestran las características ideales de un filtro de paso alto.
Se ha encontrado que los filtros de paso alto pasan frecuencias desde el punto de frecuencia de corte hasta la frecuencia “infinita”, pero esto no existe en consideraciones prácticas. Además del filtro de paso alto pasivo, la respuesta de frecuencia máxima de este filtro de paso alto activo está limitada por las características de bucle abierto del amplificador operacional.
Filtro electrónico activo de paso alto
Un filtro de paso alto activo de primer orden se obtiene conectando un circuito de filtro de paso alto RC pasivo al terminal inversor o no inversor del amplificador operacional. A continuación se muestra el circuito de filtro de paso alto RC pasivo conectado al terminal no inversor del amplificador operacional de ganancia unitaria.
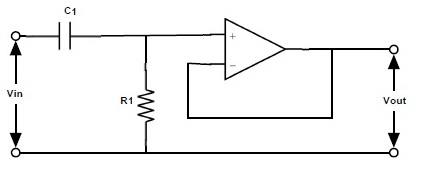
Gana AMáximo = 1 y frecuencia de corte fc = Relación 1/2πRC
Filtro activo de paso alto con alta ganancia de voltaje
Se comporta igual que un filtro pasivo de paso alto, pero la señal de entrada es amplificada por el amplificador en la salida. La cantidad de amplificación depende de la ganancia del amplificador.
La magnitud de la ganancia de la banda de paso es 1 + (R3/R2donde R3 es la resistencia de retroalimentación (unidad: Ω ohmios) y R2 es la resistencia de entrada. A continuación se muestra el circuito de un filtro de paso alto activo con función de amplificación.
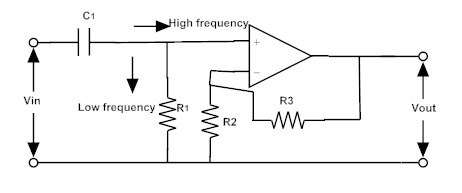
Ganancia de voltaje del filtro de paso alto activo
Ganancia de voltaje Av = AMáximo (f/fc) / √{1 + (f/fc)²}
donde f = frecuencia de funcionamiento
fc = frecuencia de corte
SerMáximo = Ganancia de banda de paso del filtro = 1 + (R3/R2)
A bajas frecuencias, es decir, cuando la frecuencia de funcionamiento es inferior a la frecuencia de corte, la ganancia de tensión es menor que la ganancia de la banda de paso AMáximoA altas frecuencias, es decir, cuando la frecuencia de funcionamiento es mayor que la frecuencia de corte, la ganancia de voltaje del filtro es igual a la ganancia de banda de paso.
Si la frecuencia de funcionamiento es igual a la frecuencia de corte, la ganancia de voltaje del filtro es igual a 0.707 A.Máximo.
Ganancia de voltaje (dB)
La magnitud de la ganancia de voltaje generalmente se expresa en decibelios (dB).
Serv(dB) = 20 log10 (Vfuera/VY)
-3 dB = 20 logs10 (0.707*Vfuera/VY)
La frecuencia de corte que separa la banda de paso de la banda de parada se puede calcular mediante la siguiente ecuación
fC = 1 / (2πRC)
El desplazamiento de fase del filtro de paso alto activo es igual al desplazamiento de fase del filtro pasivo. Esto es igual a +45° en la frecuencia de corte fC, y este valor de desplazamiento de fase es igual por:
Ø = bronceado-1(1/2πfcControl RC)
Respuesta en frecuencia del filtro de paso alto activo
A continuación se muestra la curva de respuesta de frecuencia para la ganancia de bucle abierto del amplificador.
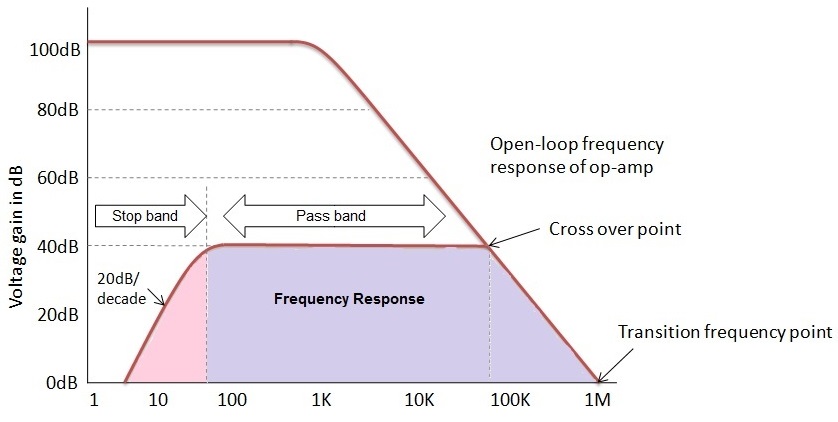
En la respuesta de frecuencia de un filtro de paso alto activo, la frecuencia máxima de la banda de paso está limitada por el ancho de banda o las características de bucle abierto del amplificador operacional. Debido a esta limitación, la respuesta de un filtro de paso alto activo se parece a la de un filtro de banda ancha.
Este filtro activo de paso alto basado en amplificador operacional se puede utilizar para lograr una alta precisión utilizando resistencias y condensadores con tolerancias bajas.
Filtro de paso alto activo mediante un amplificador operacional inversor
Se ha descubierto que los filtros activos de paso alto pueden diseñarse utilizando los terminales inversores o no inversores del amplificador operacional. Hasta ahora, hemos analizado las curvas de respuesta de los circuitos de filtro de paso alto y los filtros de paso alto activos no inversores. Ahora, echemos un vistazo a un filtro de paso alto activo que utiliza un amplificador operacional inversor.
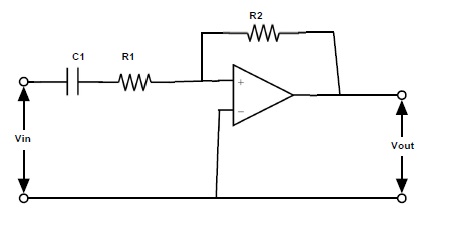
Derivación de ganancia en la forma de Laplace.
Considere un amplificador inversor como se muestra en la siguiente figura.
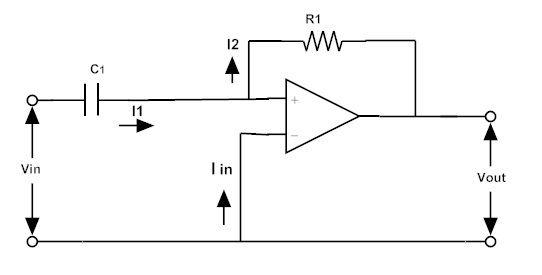
Impedancia de entrada Z1 = 1/sC1
donde s = Variable de Laplace
C1 = capacitancia
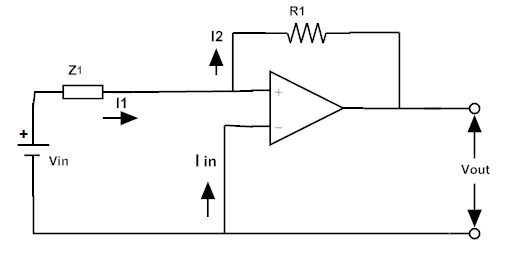
Las corrientes que fluyen a través del circuito son I1, I2, Iin,
donde I1 = I2 e Iin = 0
VY / Z1 = -Vfuera /R (R)1
Vfuera A/VY =- Investigación1 / Z1
Vfuera A/VY =- Investigación1 / (1/sC1)
Vfuera A/VY = -sR1C1 = Ganancia
Ejemplo de un filtro de paso alto activo
El valor de la frecuencia de corte es de 10 KHz y la ganancia de la banda de paso es AMáximo El valor del condensador es 1,5 y el valor del condensador es 0,02 μF.
La ecuación para la frecuencia de corte es: fC = 1 / (2πRC)
Si reordenamos esta ecuación, obtenemos R. = 1 / (2πfC)
R = 1/(2π * 10000 * 0.02 * 10-6) = 795.77 Ω
La ganancia de banda de paso del filtro es A.Máximo = 1 + (R3/R2) = 1,5
R3 = 0,5 R2
Si el valor de R2 es de 10 KΩ, entonces R3 = 5 kΩ
La ganancia del filtro se puede calcular de la siguiente manera
Ganancia de voltaje del filtro de paso alto |Vfuera A/VY |= AMáximo * (f/fc) /√[1 + (f/fc)²]
Serv(dB) = 20 log10 (Vfuera/VY)
Utilice esta fórmula para representar la respuesta del rango de frecuencia y trazar la curva de respuesta del filtro. Se supone que estas respuestas están entre 10 Hz y 100 KHz.
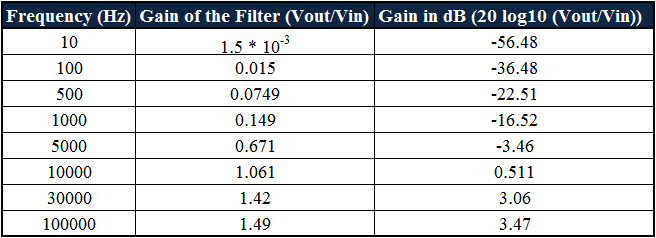
Trama de Bode
Utilice este diagrama de Bode para analizar la respuesta de frecuencia de un circuito. No es más que un gráfico de cambios de tiempo lineales y funciones de transferencia de frecuencia. Se representa en fr. logarítmico. Eje de equivalencia. Consta principalmente de dos parcelas. Uno es un gráfico de amplitud y el otro es un gráfico de fase.
El gráfico de amplitud representa la magnitud de la respuesta de frecuencia, o ganancia, mientras que el gráfico de fase se utiliza para representar la respuesta de desplazamiento de frecuencia.
A continuación se muestra el diagrama de Bode de la respuesta en frecuencia según los valores de la tabla anterior.
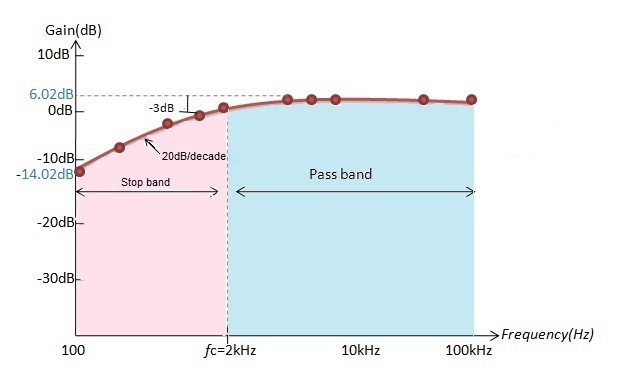
Según los valores calculados, la ganancia (dB) del filtro, que se obtiene a una frecuencia de 10 Hz, es de -56,48. Si aumenta el valor de frecuencia a 100 Hz, la ganancia obtenida será de -36,48 dB, y a una frecuencia de 500 Hz, la ganancia del filtro será de -22,51 dB.
A una frecuencia de 1000 Hz, la ganancia en dB es de -16,52. Esto significa que a medida que aumenta la frecuencia, la ganancia del filtro aumenta a una velocidad de 20 dB/década.
Hasta una frecuencia de corte de 10 KHz, la ganancia del filtro aumenta, pero más allá de la frecuencia de corte, la ganancia alcanza su valor máximo y permanece constante.
Filtro de paso alto de segundo orden
La respuesta de frecuencia del filtro activo de segundo orden es exactamente opuesta a la del filtro activo de paso bajo de segundo orden porque el filtro atenúa los voltajes por debajo de la frecuencia de corte. La función de transferencia del filtro de segundo orden se muestra a continuación
Vfuera(s)/ VY(s) = -Ks² / s² + (ω0/Q)s + ω0²
Donde: K = R1/R2 y ω0 = 1/CR
Esta es una forma común de filtrado de paso alto de segundo orden.
Filtro electrónico activo de paso alto de segundo orden
El procedimiento de diseño para un filtro activo de segundo orden es el mismo que el procedimiento de diseño para un filtro de segundo orden, ya que solo hay una variación en la caída. Si la caída del filtro de paso alto activo de primer orden es de 20 dB/década, la caída del filtro de segundo orden es de 40 dB/década.
Esto significa el doble del valor del filtro de primer orden. El circuito del filtro de segundo orden se muestra a continuación.
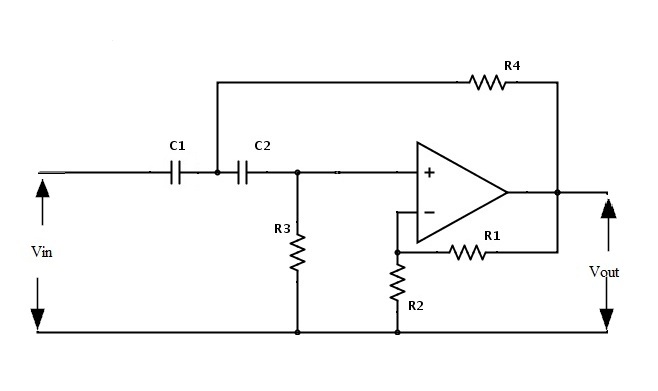
La ganancia del filtro es 1 + R1/R2, y la ecuación para la frecuencia de corte es fc = 1/2π√R3R4C1C2
Ejemplo de un filtro de paso alto activo de segundo orden
Diseñe un filtro con una frecuencia de corte de 4 KHz y una tasa de retardo de banda de parada de 40 dB/década. La tasa de retardo de la banda de parada es de 40 dB/década, por lo que está claro que este filtro es un filtro de segundo orden.
Considere el valor del condensador C1 = C2 = C = 0.02 μF
La ecuación para la frecuencia de corte es R = 1/2πfC.
Al ordenar esta fórmula, se obtiene R = 1⁄2πfC.
Sustituya el valor de la frecuencia de corte a 4 KHz y el valor del condensador a 0,02 μF.
R = 1.989 KΩ = 2 KΩ.
Supongamos que el filtro tiene una ganancia de 1 + R1/R2 = 2.
R1 / R2 = 1
R1 = R2
Por lo tanto, podemos tomar R1 = R2 = 10KΩ
Por lo tanto, el filtro resultante es el siguiente.
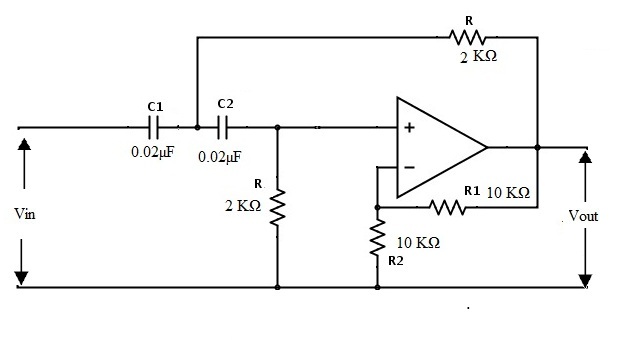
Filtro de paso alto de alto orden
Al conectar en cascada los filtros primario y secundario, se puede obtener un filtro de tercer orden. Puede conectar en cascada dos filtros de segundo orden para obtener un filtro de cuarto orden. De esta forma, con la ayuda de filtros primarios y secundarios, obtenemos un filtro de orden superior.
A medida que aumenta el orden del filtro, aumenta la diferencia entre las bandas de parada reales y teóricas. Pero como ya hemos visto que la resistencia y el condensador que determinan el valor de respuesta de frecuencia son los mismos, la ganancia general del filtro de orden superior es igual.
Este orden en cascada se muestra a continuación.
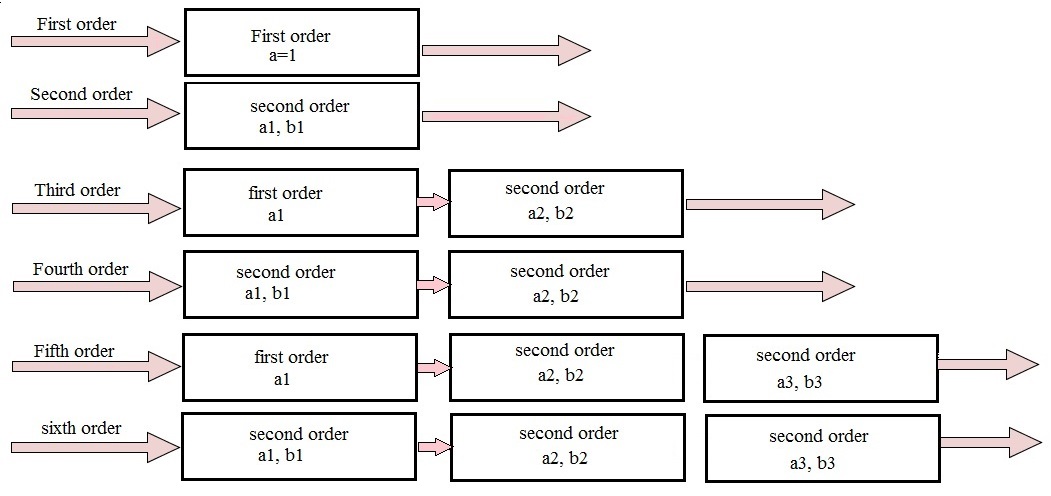
Aplicaciones de los filtros activos de paso alto
- Se utilizan en altavoces para reducir el ruido de bajo nivel.
- Para eliminar la distorsión de la vibración en las aplicaciones de audio, también se denominan filtros de refuerzo de agudos.
- Se utilizan para amplificar señales de alta frecuencia en amplificadores de audio.
- Estos también se utilizan en ecualizadores.