Un filtro Butterworth es un tipo de filtro activo que tiene una respuesta de frecuencia relativamente plana en toda la banda de paso. Debido a esta respuesta frecuente, los filtros Butterworth también se conocen como filtros planos máximos o filtros planos-planos.
La tecnología de filtro Butterworth le permite diseñar todo tipo de filtros, incluidos los de paso alto, paso bajo y paso de banda. En este tutorial, nos centraremos en el diseño de un filtro de paso bajo utilizando la tecnología de filtro Butterworth.
Para obtener más información sobre los filtros de paso bajo en general, ya sean activos o pasivos, lea los siguientes tutoriales:Filtros RC pasivos de paso bajoyFiltro de paso bajo activo“.
Tabla de contenido
- Introducción
- Filtro Butterworth
- Aproximación de Butterworth
- Filtro primario de paso bajo Butterworth
- Filtro Butterworth de paso bajo de segundo orden
- Respuesta de frecuencia ideal de los filtros Butterworth.
- Polinomio de filtro Butterworth de paso bajo normalizado
- Ejemplo de un filtro de paso lento de Butterworth
- Filtro de paso bajo Butterworth de tercer orden
- aplicación
- Artículos Relacionados:
Introducción
Hay tres consideraciones principales en el diseño de un circuito de filtro.
- La respuesta de la banda de paso debe ser de máxima planitud.
- Se requiere una transición lenta de la banda de paso a la banda de parada.
- La capacidad de un filtro para pasar una señal sin distorsión en la banda de paso.
Estas distorsiones suelen ser causadas por cambios de fase en la forma de onda. Además de estos tres, los parámetros de los tiempos de subida y bajada también juegan un papel importante. Para cada consideración, estas consideraciones se tienen en cuenta para diseñar un tipo de filtro.
El filtro Butterworth está diseñado para ofrecer la máxima respuesta plana. Diseñamos un filtro Chebyshev para una transición suave de la banda de paso a la banda de parada, y un filtro Bessel para un retardo de tiempo plano máximo.
Filtro Butterworth
A expensas de la inclinación del medio de transición de la banda de paso a la banda de parada, este filtro Butterworth proporciona una respuesta plana a la señal de salida. Es por eso que también se le llama filtro de amplitud plana máxima.
La velocidad de la respuesta de atenuación del filtro está determinada por el número de polos adquiridos en el circuito. El número de polos depende del número de elementos reactivos en el circuito, es decir, el número de inductores o condensadores utilizados en el circuito.
La respuesta de amplitud del filtro Butterworth de enésimo orden se da como:
Vfuera A/VY = 1 / √{1 + (f / fc)2n}
donde “n” es el número de polos en el circuito. A medida que aumenta el valor de “n”, también lo hace la planitud de la respuesta del filtro.
‘f’ = frecuencia de funcionamiento del circuito, ‘fc‘ = frecuencia central o frecuencia de corte del circuito.
Estos filtros están predeterminados con consideraciones de aplicación, principalmente en circuitos RC activos con altas frecuencias. Aunque no ofrece una respuesta de corte brusca, a menudo se considera un filtro versátil utilizado en muchas aplicaciones.
Aproximación de Butterworth
Sabemos que se necesita un filtro de orden superior para satisfacer las consideraciones de respuesta del filtro y obtener una aproximación cercana al filtro ideal, por lo que tenemos lo siguiente: Esto añade complejidad.
También se conocen la frecuencia de salida y las respuestas de fase de los circuitos de paso bajo y paso alto. Las características ideales del filtro son la máxima planitud, la máxima ganancia de banda de paso y la máxima atenuación de la banda de parada.
Para diseñar un filtro, se necesita una buena función de transferencia. Para satisfacer estas funciones de transferencia, la derivación matemática se realiza en un diseño de filtro analógico con muchas funciones aproximadas.
En este diseño, el filtro Butterworth es uno de los tipos de filtro. Las consideraciones de diseño de paso bajo de Butterworth se utilizan principalmente para una serie de funciones. Más adelante, discutiremos el polinomio normalizado del filtro de paso bajo de Butterworth.
Filtro primario de paso bajo Butterworth
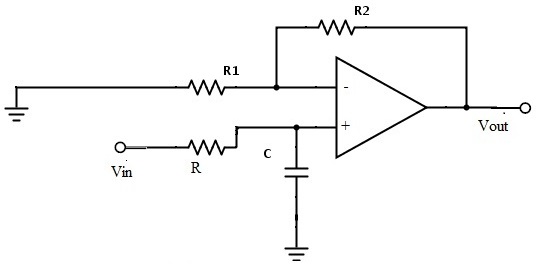
El siguiente circuito muestra un filtro Butterworth de paso bajo.
La ganancia de banda de paso requerida para un filtro Butterworth depende principalmente de los valores de resistencia de R1 y Rf, y la frecuencia de corte del filtro depende de los elementos R y C del circuito anterior.
La ganancia del filtro se da como A_max = 1 + R1 / Rf.
La impedancia del condensador ‘C’ viene dada por -jX.C El voltaje a través del condensador se da de la siguiente manera:
Vc =-jXC / (R – jXC) * Vin.
donde XC = 1 / (2πfc), reactancia capacitiva.
La función de transferencia de la forma polar del filtro se da de la siguiente manera:
H(jω) = |Vout/Vin|∟ø
donde la ganancia del filtro es Vfuera A/VY = AMáximo / √{1 + (f/fH)²}
Ángulo de fase Ø = – tan-1 (f/fH )
Baja frecuencia significa que si la frecuencia de funcionamiento es inferior a la frecuencia de corte, la ganancia de la banda de paso es igual a la ganancia máxima.
Vfuera A/VY = AMáximo En otras palabras, es una constante.
Una frecuencia más alta significa que la ganancia es menor que la ganancia máxima cuando la frecuencia de funcionamiento es mayor que la frecuencia de corte.
Vfuera A/VY <Máximo
Si la frecuencia de funcionamiento es igual a la frecuencia de corte, entonces la función de transferencia es igual a Amax/√2. La reducción de ganancia es de 20 dB/década o 6 dB/octava, que puede expresarse como -20 dB/década en la pendiente de respuesta.
Filtro Butterworth de paso bajo de segundo orden
Una red RC adicional conectada al filtro primario de Butterworth proporciona un filtro de paso bajo secundario. Este filtro de paso bajo de segundo orden tiene la ventaja de que la ganancia disminuye muy rápidamente en la banda de parada después de la frecuencia de corte.
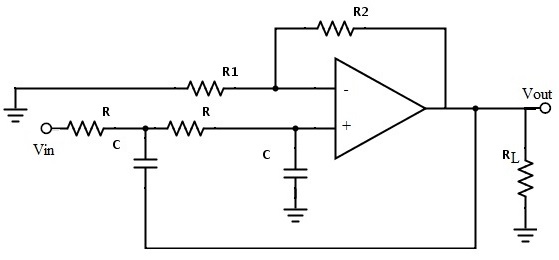
En este filtro de segundo orden, el valor de la frecuencia de corte depende de los valores de las resistencias y condensadores en las dos secciones RC. La frecuencia de corte se calcula mediante la siguiente fórmula:
fc = 1 / (2π√R2C2)
La ganancia disminuye a una velocidad de 40 dB/década, y la respuesta está representada por una pendiente de -40 dB/década. La función de transferencia del filtro puede venir dada por:
Vfuera A/VY = AMáximo / √{1 + (f/fc)4}
La forma estándar de la función de transferencia de un filtro de segundo orden viene dada por:
Vfuera A/VY = AMáximo /segundo2 + 2εωns + ωn2
Donde: ωn = Frecuencia natural de oscilación = 1/R2C2
ε = coeficiente de amortiguamiento = (3 – AMáximo ) / 2
Para un filtro de Butterworth de segundo orden, a partir del polinomio de Butterworth normalizadoEl término intermedio requerido es sqrt(2) = 1.414.
3 – UnMáximo = √2 = 1,414
Para garantizar la respuesta del filtro de salida, se obtiene una ganancia AMáximo es de 1.586.
Un filtro Butterworth de orden superior se obtiene mediante la conexión en cascada de los filtros Butterworth primario y secundario. Esto se puede ver de la siguiente manera:
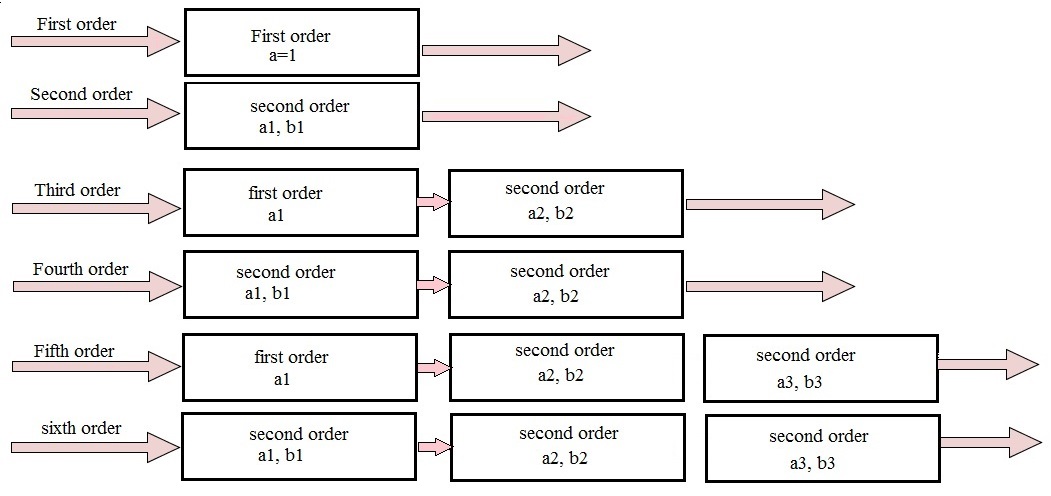Aquín y bn son coeficientes de filtro predeterminados que se utilizan para generar la función de transferencia requerida.
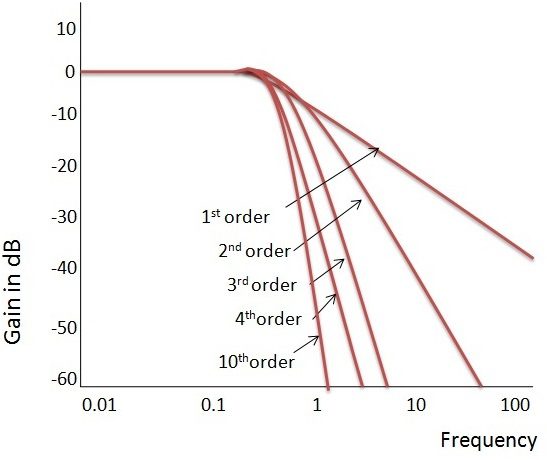
Respuesta de frecuencia ideal de los filtros Butterworth.
La planitud de la respuesta de salida aumenta a medida que aumenta el orden del filtro. A continuación se muestran la ganancia y la respuesta normalizada del filtro Butterworth para diferentes grados.
Polinomio de filtro Butterworth de paso bajo normalizado
La normalización es el proceso de dividir el voltaje, la corriente o la impedancia por cantidades en la misma unidad de medida. Este proceso se utiliza para crear un rango o nivel adimensional de un valor determinado.
El polinomio denominador de la función de transferencia de filtro da el polinomio de Butterworth. Dado un plano s en un círculo de igual radio con el centro en el origen, todos los polos del filtro de Butterworth están en la mitad izquierda de ese plano s.
Para cualquier filtro de orden, el coeficiente siempre debe ser 1 a la potencia máxima de ‘s’, y para cualquier filtro de grado, el término constante es siempre 1. Para los filtros de orden par, todos los factores polinómicos son inherentemente cuadráticos. En el caso de los filtros de orden impar, todos los polinomios, excepto los filtros de primer orden, son de segundo orden, y en el caso de los filtros de primer orden, los polinomios son 1+s.
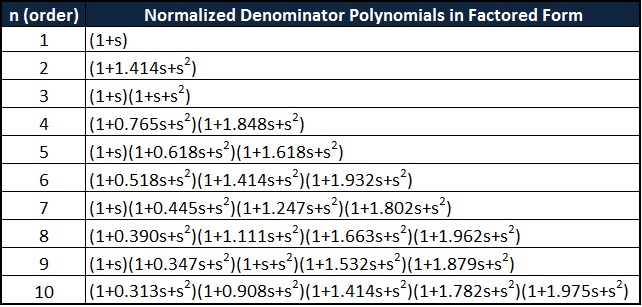
El polinomio de Butterworth en forma de coeficiente se resume en la tabla de la siguiente manera:
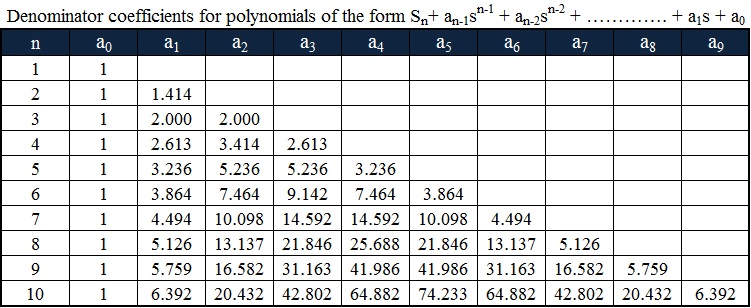
La función de transferencia del filtro Butterworth de enésimo orden se da como:
H(jω) = 1/√{1 + ε² (ω/ωc)2n}
donde n es el orden del filtro
ω es la frecuencia en radianes, igual a 2πf
Y ε es la ganancia máxima de la banda de paso Amax
Ejemplo de un filtro de paso lento de Butterworth
Considere un filtro de paso bajo Butterworth con una frecuencia de corte de 15,9 kHz, una ganancia de banda de paso de 1,5 y un condensador de C = 0,001 μF.
fc = Relación 1/2πRC
15,9 * 10³ = 1 / {2πR1 * 0,001 * 10-6}
R = 10kΩ
SerMáximo = 1,5 y suponiendo que R1 es de 10 kΩ
SerMáximo = 1 + {Rf /R (R)1}
Rf = 5kΩ
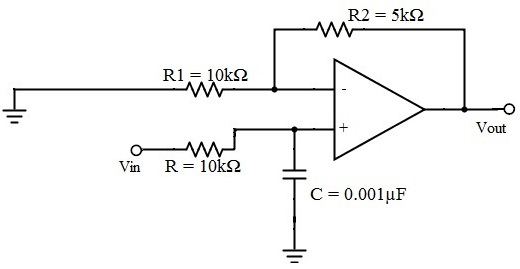
Filtro de paso bajo Butterworth de tercer orden
La cascada de filtros Butterworth primarios y secundarios da como resultado un filtro Butterworth de tercer orden. A continuación se muestra el circuito de filtro Butterworth de tercer orden.
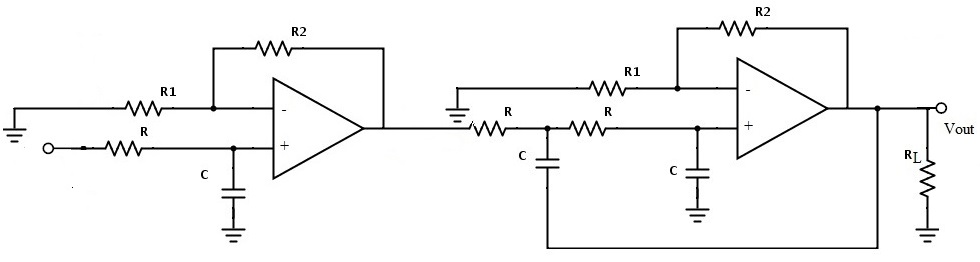
Para un filtro cúbico de paso bajo, el polinomio del polinomio de Butterworth de paso bajo normalizado especificado es (1+s) (1+s+s²). Este filtro contiene tres coeficientes desconocidos, que son0 Ser1 Ser2.
Estos valores de coeficiente son:0 = 1、1 = 2 y a2 = 2. La planitud de la curva aumenta en este filtro Butterworth de tercer orden en comparación con el filtro de primer orden.
aplicación
- Debido a la naturaleza de la banda máxima de paso plano, se utiliza como filtro antialiasing en aplicaciones de conversión de datos.
- Se ha aplicado al radar, como el diseño de pantalla de los camiones de objetivos de radar.
- En aplicaciones de audio de alta calidad, se utilizan.
- Se utilizan en filtros digitales para el análisis de movimiento.