Los fasores son una forma efectiva de analizar el comportamiento de los elementos en los circuitos de CA dadas las mismas frecuencias de circuito. El resultado de sumar dos fasores está determinado por su fase relativa, ya sea que estén “en fase” o “fuera de fase” según la diferencia de fase.
Una forma de onda sinusoidal es una cantidad alterna que se puede representar gráficamente en el dominio del tiempo a lo largo del eje horizontal. Como una cantidad que varía con el tiempo, una forma de onda sinusoidal tiene un valor positivo máximo en algún punto. π/2el valor negativo máximo en el tiempo 3π/2donde se producen valores cero a lo largo de la línea de base. 0, Pi y 2pi punto.
Sin embargo, no todas las formas de onda sinusoidales pasan por el punto del eje cero exactamente al mismo tiempo y pueden “desplazarse” a la derecha o a la izquierda del punto del eje cero. 0ah Cuando se compara con otra onda sinusoidal, difiere en cierto valor.
Por ejemplo, compare formas de onda de voltaje y corriente. Esto provoca una desalineación angular y diferencia de fase Entre dos formas de onda sinusoidales.una onda sinusoidal que no pasa por cero t = 0 Hay un cambio de fase.
La diferencia o cambio de fase de una forma de onda sinusoidal es un ángulo. Φ (letra griega phi), expresada en grados o radianes que una forma de onda se desplaza desde un punto de referencia dado a lo largo del eje cero horizontal. En otras palabras, el cambio de fase es la diferencia lateral entre dos o más formas de onda a lo largo de un eje común, y las formas de onda sinusoidales de la misma frecuencia pueden experimentar diferencias de fase.
diferencia de fase, Φ La forma de onda de CA cambia de la siguiente manera. 0 hasta un plazo máximo de t Una forma de onda durante un ciclo completo. Puede estar en cualquier lugar a lo largo del eje horizontal entre: Φ=0~2π (radianes) o Φ=0~360ah Depende de las unidades angulares utilizadas.
La diferencia de fase también se puede expresar como cambio de hora de τ parte de la duración en segundos, t Por ejemplo, +10mS o –50uS, pero es común expresar la diferencia de fase como una medida angular.
Luego, la ecuación para el valor instantáneo de la forma de onda sinusoidal de voltaje o corriente creada por la forma de onda sinusoidal anterior debe modificarse para tener en cuenta el ángulo de fase de la forma de onda, y esta nueva expresión general se convierte en:
Tabla de contenido
fórmula de diferencia de fase
- dónde:
- ametros – es la amplitud de la forma de onda.
- ωt – es la frecuencia angular de la forma de onda en radianes/segundo.
- Φ (phi) – El ángulo de fase (en grados o radianes) por el cual la forma de onda se desplaza hacia la izquierda o hacia la derecha desde el punto de referencia.
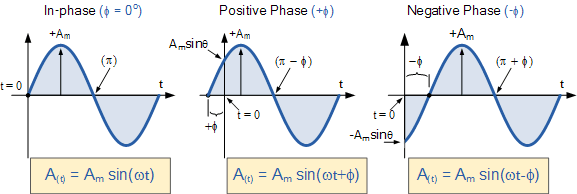
Si la pendiente positiva de la forma de onda sinusoidal pasa por el eje horizontal “hacia adelante” t = 0 Luego, la forma de onda se desplazó hacia la izquierda, por lo que Φ >0el ángulo de fase será de naturaleza positiva. +Φ Da el ángulo de fase principal. En otras palabras, aparece antes de 0 en el tiempo.ah Genera una rotación en sentido antihorario de un vector.
De manera similar, suponga que la pendiente positiva de una forma de onda sinusoidal pasa por el eje x horizontal en algún punto “después”. t = 0 Luego, la forma de onda se desplazó hacia la derecha, por lo que Φ<0el ángulo de fase será inherentemente negativo -Φ Dado que aparece después de 0 en el tiempo, produce un ángulo de fase retrasado.ah Genera una rotación en el sentido de las agujas del reloj de un vector. Ambos casos se muestran a continuación.
Relación de fase de onda sinusoidal
Primero, considere dos cantidades alternas, como el voltaje. v y actual, I tener la misma frecuencia F en hercios. Como la frecuencia de las dos cantidades es la misma que la velocidad angular, ω debe ser lo mismo. Por lo tanto, en cualquier momento, se puede decir que la fase de voltaje es v Estará en fase con la corriente. I.
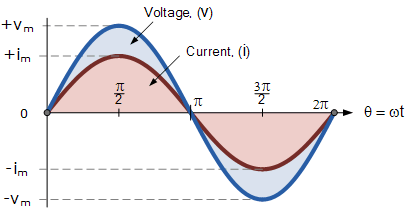
En este caso, el ángulo de rotación dentro de un período dado siempre será el mismo y la diferencia de fase entre las dos cantidades cambiará. v y I por lo tanto será cero, Φ = 0. Para la frecuencia de voltaje, v y ahora, I Deben ser iguales y ambos deben alcanzar sus valores máximos positivo, negativo y cero simultáneamente durante un ciclo completo (aunque sus amplitudes pueden ser diferentes). Entonces dos cantidades alternas, v y I Se dice que está “en fase”.
Dos ondas sinusoidales – “en fase”
Ahora consideremos el voltaje. v y ahora, I hay una diferencia de fase entre ellos 30ahentonces (Φ = 30ah de nuevo Pi/6 radianes). Dado que ambas cantidades alternas giran a la misma velocidad, es decir, tienen la misma frecuencia, esta diferencia de fase permanece constante en todos los instantes de tiempo, en cuyo caso la diferencia de fase es 30ah Entre las dos cantidades se denota por phi y Φ Como se muestra abajo.
Diferencia de fase de onda sinusoidal
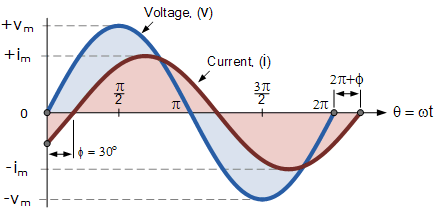
La forma de onda de voltaje anterior comienza en cero a lo largo del eje de referencia horizontal, pero la forma de onda de corriente en el mismo instante sigue siendo negativa y no se cruza hasta que cruza este eje de referencia. 30ah más tarde. Entonces hay una diferencia de fase entre las dos formas de onda cuando la corriente alcanza su pico máximo en el eje de referencia horizontal y alcanza el valor cero después de la forma de onda de voltaje.
Dado que las dos formas de onda ya no están “en fase”, deben estar “fuera de fase” en una cantidad determinada por phi. Φ En este ejemplo esto es 30ah. Así que las dos formas de onda se ven así: 30ah fuera de fase. También se puede decir que la forma de onda de corriente va a la zaga de la forma de onda de voltaje por el ángulo de fase. Φ.En el ejemplo anterior, las dos formas de onda son diferencia de fase de retraso Entonces, las ecuaciones de voltaje y corriente anteriores se convierten en:
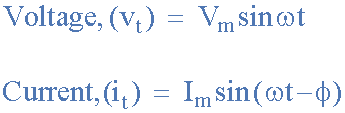
Actualmente, I Voltaje “retrasos” v por ángulo de fase Φ
Del mismo modo, para la corriente, I tiene un valor positivo, se cruza con el eje de referencia y alcanza su valor pico máximo y su valor cero en algún punto antes del voltaje. v En ese caso, la forma de onda actual “adelanta” el voltaje por un ángulo de fase. En este caso, se dice que las dos formas de onda tienen las siguientes propiedades: diferencia de fase principal Las ecuaciones para voltaje y corriente son:
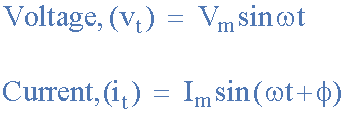
Actualmente, I “conduce” el voltaje v por ángulo de fase Φ
El ángulo de fase de una onda sinusoidal es la diferencia entre una onda sinusoidal y otra, utilizando los términos “adelanto” y “retraso” para describir la relación entre dos formas de onda sinusoidales de la misma frecuencia trazadas en el mismo eje de referencia. para describir la relación entre . En el ejemplo anterior, las dos formas de onda son: fuera de fase A 30ah.Por lo tanto es correcto decir I será tarde v o puedes decir v dirigir I A 30ah Depende de cuál elijas como criterio.
La relación entre las dos formas de onda y el ángulo de fase resultante se puede medir en cualquier lugar a lo largo del eje cero horizontal donde cada forma de onda pasa en la dirección positiva o negativa de la “misma pendiente”.
En los circuitos de alimentación de CA, esta capacidad para describir la relación entre las sinusoides de tensión y corriente en el mismo circuito es muy importante y constituye la base del análisis de circuitos de CA.
forma de onda coseno
Ahora puede saber si la forma de onda se ha “desplazado” hacia la derecha o hacia la izquierda. 0ah En comparación con otra onda sinusoidal, la fórmula para esta forma de onda es: ametros sen(ωt± Φ). Sin embargo, si la forma de onda cruza el eje cero horizontal con una pendiente positiva, 90ah de nuevo Pi/2 radián Antes Forma de onda de referencia, esa forma de onda se llama . forma de onda coseno y expresión.
fórmula del coseno
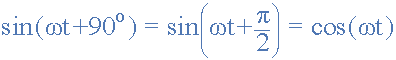
de onda cosenose llama simplemente “cos” y es tan importante en ingeniería eléctrica como la onda sinusoidal. La onda coseno tiene la misma forma que la onda sinusoidal correspondiente, es decir, una función de onda sinusoidal, pero desplazada de la siguiente manera: +90ah O un trimestre completo antes del período.
Diferencia entre ondas seno y coseno
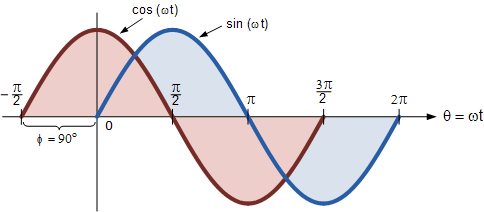
Alternativamente, podemos decir que la onda sinusoidal es la onda coseno desplazada en la otra dirección. -90ah. En cualquier caso, las siguientes reglas siempre se aplican cuando se trata de ondas angulares de seno o coseno:
Relación entre las ondas seno y coseno
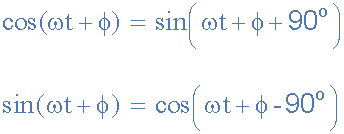
Cuando se comparan dos formas de onda sinusoidales, es más común expresar la relación como un seno o coseno de amplitud positiva, lo que se logra utilizando las siguientes identidades matemáticas:
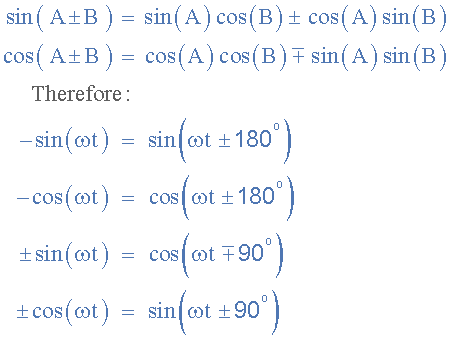
Usando la relación anterior, podemos convertir cualquier forma de onda sinusoidal, ya sea de seno a coseno o viceversa, con o sin ángulo o diferencia de fase.
En el siguiente tutorial sobre fasores, exploraremos una forma gráfica de expresar o comparar la diferencia de fase entre dos sinusoides mediante el examen de la representación fasorial de cantidades de CA monofásicas junto con el álgebra fasorial, que implica la suma matemática de dos o más fasores. uso

