Tabla de contenido
introducción
Entre todas las formas de onda, la onda sinusoidal se utiliza con frecuencia debido a su facilidad de representación y varias propiedades ventajosas. Una onda sinusoidal u onda sinusoidal es una curva que representa vibraciones suaves y repetitivas. Una onda sinusoidal se puede definir como una forma de onda cuya amplitud es siempre proporcional al seno del ángulo de desplazamiento en cada momento.
Todas las ondas se pueden crear sumando ondas sinusoidales. Una onda sinusoidal tiene un patrón que se repite. La longitud de esta porción repetida de la onda sinusoidal se llama longitud de onda.
La forma más básica en función del tiempo
Y
dónde
A es la amplitud,
F es la frecuencia;
ω = 2πf, frecuencia angular,
φ es la fase
Volver a la cima
Generando una onda sinusoidal
Hay varias formas de generar una onda sinusoidal. Se muestran a continuación.
- Oscilador de cristal
- oscilador de resistencia negativa
- generador de CA básico de bobina simple
- oscilador de cambio de fase
- Oscilador de puente Wein, etc.
El método básico para generar ondas sinusoidales es el “generador básico de bobina simple” explicado en el artículo anterior “Teoría de CA”.
Volver a la cima
¿Qué son las RPM?
RPM significa “Revolución por minuto”. En otras palabras, la “velocidad de rotación de la bobina” se denomina “RPM”. Por ejemplo, si el eje de un motor gira a 100 revoluciones por minuto, se dice que la velocidad del motor es de 100 RPM.
El número de polos es siempre par.
La relación entre la velocidad de rotación de la bobina, la frecuencia de la onda sinusoidal generada y el número de polos es la siguiente.
En términos generales, ω = 2π.Fpero si la rotación es causada por los polos magnéticos, entonces la velocidad angular se escribe como:
ω = (2/n) [2πf] dónde norte representa el número de polos
Como sabes, n = 60 Fdespués
El número de revoluciones se puede escribir como:
norte pag =(2×60)f/p
ωrotor=(2/polo)×2πf(radianes/seg)
nortepag=120f/polo(RPM)
dónde
ω es la velocidad angular de la onda sinusoidal
N es el número de polos.
F es la frecuencia de la forma de onda.
π es una constante con valor 3,1416.
El número de polos y la velocidad de una máquina de frecuencia de 60 Hz son:
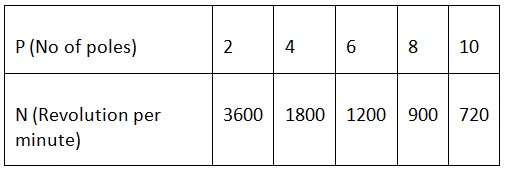
El número de polos y la velocidad de una máquina de frecuencia de 50 Hz son:
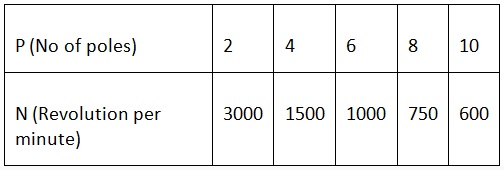
Volver a la cima
voltaje instantáneo
El voltaje instantáneo es el voltaje entre dos puntos en un momento específico en el tiempo. El voltaje de una forma de onda en un momento determinado se llama “voltaje instantáneo”.
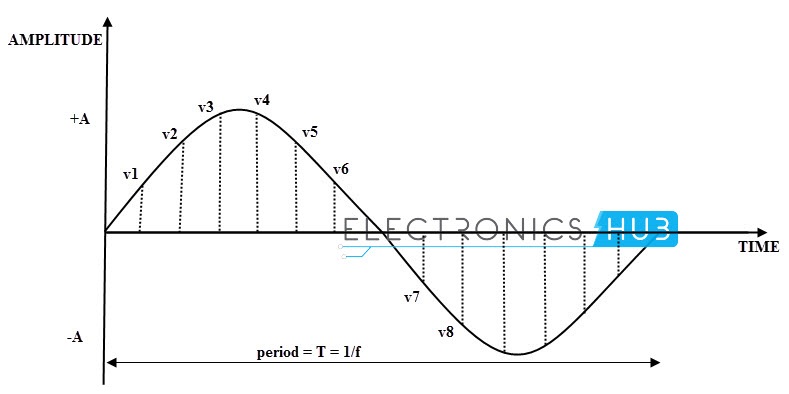
En el diagrama anterior, v1, v2, v3, v4, v5, v6… son voltajes de onda sinusoidal instantánea.
La determinación del valor instantáneo de voltaje de una onda sinusoidal depende del voltaje máximo de la onda sinusoidal.
Tensión instantánea = tensión máxima x senθ
Vinst = Vmáx × senθ
Volver a la cima
Desplazamiento de una bobina en un campo magnético.
El desplazamiento de la onda sinusoidal está determinado por el ángulo de rotación de la bobina. Está representado por “θ”. De hecho, para encontrar el voltaje instantáneo, multiplique el voltaje máximo o voltaje pico a pico de la onda sinusoidal por el seno del ángulo de rotación de la bobina.
El ángulo de rotación de la bobina en el campo magnético es θ = ωt
dónde
ω es la velocidad angular de la onda sinusoidal
t es el período de la onda sinusoidal.
Para un valor conocido del voltaje máximo de una onda sinusoidal, se puede calcular el voltaje instantáneo a lo largo de la forma de onda. El valor instantáneo da el valor de posición de la onda sinusoidal, por lo que se puede trazar un gráfico sobre la onda sinusoidal. Esto le da la forma de una onda sinusoidal.
El diagrama de arriba muestra la amplitud de una onda sinusoidal. En la Figura (1), la armadura en el campo magnético se mueve con gran amplitud, por lo que la onda sinusoidal generada forma un semiciclo positivo. Sin embargo, en la Figura (2), la armadura en el campo magnético se mueve con baja amplitud, por lo que la onda sinusoidal generada forma un semiciclo negativo.
Para entender esto fácilmente, traza el valor instantáneo de la onda sinusoidal cada 45 grados. En un ciclo completo, puedes obtener 8 valores por cada 45 grados de ángulo.
Volver a la cima
estructura sinusoidal
Si trazas una gráfica de 0° a 360° en diferentes instancias de una bobina giratoria en un campo magnético, puedes dibujar un patrón sinusoidal. Esto significa que si la fase de la onda sinusoidal es 00, 1800 y 360 0, la amplitud de la onda sinusoidal es 0, lo que significa que no se induce ninguna EMF en la bobina giratoria.
Esto se debe a que ninguna parte de la bobina móvil se ve afectada por las líneas de flujo magnético. CEM cero inducido en las ubicaciones A y E. De manera similar, en las fases 900 y 2700, la onda sinusoidal tiene una amplitud máxima. Ocurre en C&G.
En otras posiciones de la onda sinusoidal (B, D, F, H), la FEM sigue la fórmula e = Vmax*sinθ.
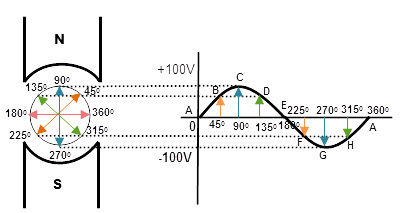
El valor de la fuerza electromotriz de la onda sinusoidal con respecto al ángulo de fase de la bobina móvil es el siguiente.
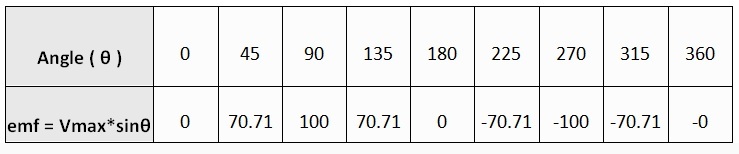
Por lo tanto, la onda sinusoidal tiene un valor de amplitud alto (positivo) en 900 y un valor de amplitud alto (negativo) en 2700.
Volver a la cima
Velocidad angular de la onda sinusoidal
Ésta es la tasa de cambio del desplazamiento angular con respecto al tiempo. La “velocidad angular” es una medida de la tasa de cambio de la posición angular de un objeto durante un período de tiempo. Está representado por ω.
Es una cantidad vectorial.Unidades de velocidad angular: radianes o grados
ω = 2π f (radianes/segundo)
Dado que la frecuencia de la corriente alterna india es de 50 Hz, la velocidad angular se puede medir como 314,16 rad/seg.
La velocidad angular se define como la velocidad del movimiento circular de la bobina del alternador.
Como ya se explicó anteriormente, se denota por ω. Es función de la duración de la onda sinusoidal, o el tiempo que tarda en completar una revolución (T).
Sabemos que la frecuencia es inversamente proporcional al período de tiempo de una onda sinusoidal. es decir f = 1/T. Esto da la velocidad angular de la onda sinusoidal en el período de tiempo como:
ω=2 π / T (rad/s)
De la ecuación anterior, podemos decir que la velocidad angular de una onda sinusoidal es inversamente proporcional al período de tiempo de la onda sinusoidal. Es decir, cuanto mayor sea el valor del período, menor será la velocidad angular y viceversa.
Ejemplo de onda sinusoidal
Si la onda sinusoidal se define como Vmε = 150 sen (220t), encuentre su velocidad y frecuencia RMS y la velocidad instantánea de la forma de onda después de 5 ms.
Resuelto:
La fórmula general para una onda sinusoidal es Vt = Vm sin (ωt).
Comparando esto con la ecuación dada Vmâ = 150 sen (220t), obtenemos
El voltaje máximo de voltaje máximo es de 150 voltios.
La frecuencia angular es de 220 radianes/segundo.
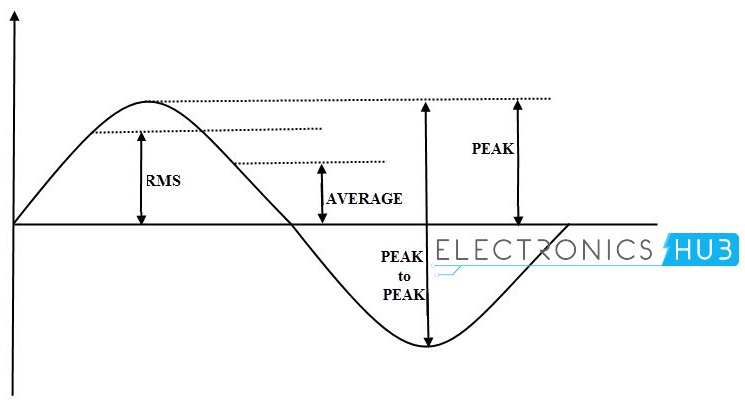
La velocidad RMS de la forma de onda viene dada por:
Vrms = 0,707 x amplitud máxima o valor pico.
= 0,0707 x 150 = 106,05 voltios
Como conocemos la velocidad angular de la onda sinusoidal, el ángulo de la onda sinusoidal es función de la frecuencia y podemos conocer la frecuencia de la forma de onda. Usando la relación entre ω y f
Velocidad angular (ω) =
Frecuencia (f) = ω / 2 π
Para una forma de onda sinusoidal dada ω = 220,
Frecuencia = 220 / 2 π
= 220 / (2 x 3,1416)
= 220/6,2832
= 35,0140 Hz
El valor instantáneo después de 5 ms se puede calcular utilizando la siguiente fórmula.
Vi = 150 sen (220 x 5 ms)
= 150 pecados (1.1)
= 150 × 0,019
= 133,68 voltios
La fase del ángulo en el instante t = 5 ms se calcula en radianes. Puedes convertir valores en radianes a valores en grados muy fácilmente. La fórmula para convertir radianes a grados es:
Grados = (1800/π)×radianes
1.1 Conversión de radianes a grados:
= (1800 / π) × 1,1
= 63,02 grados
Volver a la cima