Un inductor suele ser una bobina de alambre que crea un campo magnético alterno a su alrededor cuando una corriente alterna fluye a través de él. La inductancia es la propiedad de un inductor que resiste cambios de corriente. Medido en henrios. Esta inductancia induce una fuerza contraelectromotriz en la bobina cuando se somete a corriente alterna.
[adsense1]
Según la ley de Lenz, esta fem se opone al cambio de corriente. Por lo tanto, dado que no hay resistencia en el circuito, el voltaje aplicado solo necesita superar esta contrafem. Por lo tanto, el voltaje aplicado y la fuerza contraelectromotriz deben ser iguales y opuestos para mantener la corriente fluyendo a través del circuito.
Los circuitos de CA que utilizan inductores funcionan de manera muy diferente a los circuitos de CC. En este caso, la corriente que fluye a través de la bobina depende no sólo de la inductancia, sino también de la frecuencia de la fuente de alimentación de CA. Explique brevemente el funcionamiento de circuitos de CA con cargas inductivas.
Tabla de contenido
Aplicar CA a un inductor puro
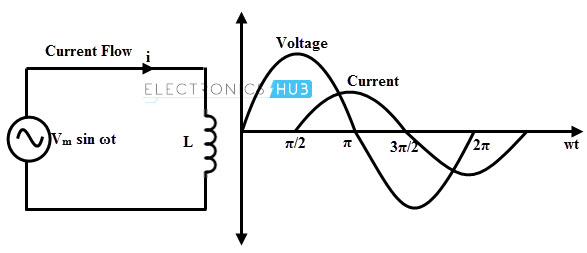
Un inductor puro no tiene resistencia en el devanado de la bobina, sólo inductancia. Esta característica de inductancia la exhiben todos los motores, transformadores y generadores (con cierta resistencia en la bobina). La siguiente figura muestra un circuito inductivo puro con una fuente de voltaje de CA y su forma de onda apropiada.
[adsense2]
Sea el voltaje aplicado v = V.metros Pecado ωt. Como se mencionó anteriormente, la fem inducida es igual al voltaje aplicado y viceversa. Es decir, v = – e
donde e es la fuerza contraelectromotriz y es igual a -L di/dt.
Sustituyendo la expresión eMF se obtiene:
v = Ldi/dt
Vmetros sen ωt = L di/dt
Di = (Vmetros / L) sen ωt dt
Aplicando la integral en ambos lados nos da:
yo = (Vmetros / L) ∫ sen ωt dt
= (Vmetros / ωL) (-cos ωt)
yo = (Vmetros / wL) (sen ωt – π/2)
Cuando (sen ωt – π/2) es 1, la corriente máxima fluye en el circuito.Entonces
soy = (Vmetros /ωL)
Entonces la ecuación actual queda:
yo = yometros pecado (ωt – π/2)
Dónde estoymetros = (Vmetros /ωL)
De las ecuaciones de corriente y voltaje anteriores, está claro que la corriente está retrasada con respecto al voltaje en 900 grados. Por lo tanto, en un circuito inductivo puro, la corriente está en cuadratura con el voltaje, como se muestra en la forma de onda anterior.
Esto significa que cuando el cambio de corriente es máximo (cuando la corriente pasa por cero), el voltaje inducido a través del inductor es máximo. De manera similar, en el valor máximo de la corriente, donde la corriente no cambia, el voltaje inducido a través del inductor es cero.
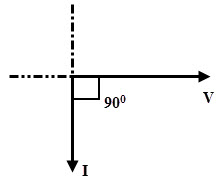
Por lo tanto, el voltaje a través de un inductor hace avanzar la corriente a través de ese inductor en un cuarto (cuarto) de ciclo. A continuación se muestra el diagrama fasorial de un circuito de CA inductivo puro.
reactancia inductiva
De la derivación anterior, la ecuación de corriente máxima queda como:
Imetros = (Vmetros /ωL)
ωL=Vmetros / Imetros
Esta relación de voltaje y corriente es la opuesta al flujo de corriente por un circuito inductivo. Esta cantidad de wL se llama reactancia inductiva y se mide en ohmios y se denomina XL.
La reactancia inductiva de un circuito de CA se puede expresar como:
XL = ωL = 2ΠfL (porque ω = 2Πf)
donde XL es la reactancia inductiva en ohmios.
f es la frecuencia de la tensión de alimentación
L es la inductancia de la bobina Henry.
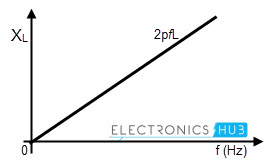
La ecuación anterior muestra que a medida que aumenta la frecuencia de la fuente de entrada, la tasa de cambio de la corriente también cambia. Por lo tanto, aumenta la fem inducida (o voltaje de reacción) a través del inductor.
Como resultado, se reduce la corriente neta que fluye a través del inductor. Como se muestra en la figura, se puede concluir que la reactancia del inductor varía linealmente con la frecuencia de la fuente de alimentación.
Potencia y factor de potencia en circuitos de CA inductivos.
La potencia en un circuito de CA es el producto del voltaje y la corriente instantáneos.Esto se da como
P = v × yo
P = Vmetros pecado ωt×Imetros Pecado (ωt – 90)
Integración a lo largo del ciclo
P = Vmetros pecado ωt×Imetros Pecado (ωt – 90)
P = 1/2π (∫02π Vmetros pecado ωt×Imetros pecado (ωt – 90) dωt)
= (Vmetros Imetros / 2π) (∫02π sen ωt × (-cos ωt) dwt)
= (Vmetros Imetros / 2π) (∫02π (-sen 2 ωt)/2 dwt)
= (Vmetros Imetros / 8π) (cos 4π – cos 0)
= (Vmetros Imetros / 8π) (1 – 1)
P=0
La potencia promedio en un inductor puro siempre es cero porque la cantidad de energía recibida de la fuente en un medio ciclo regresa a la fuente en el siguiente medio ciclo.
La siguiente figura muestra la curva de potencia de un circuito de CA inductivo. La potencia positiva es igual a la potencia negativa, por lo que la potencia resultante durante un ciclo es cero. Esto explica claramente que la inductancia pura no disipa potencia.
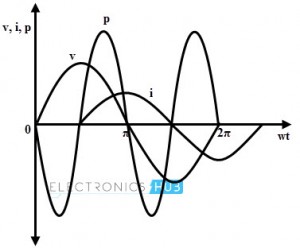
En este circuito, la corriente también es sinusoidal, pero está retrasada 90 grados con respecto al voltaje. Dado que la corriente está retrasada con respecto al voltaje 90 grados,0diferencia de fase, θ es igual a 900.después
Factor de potencia, cos 90 = 0
El factor de potencia de un circuito inductivo puro es cero, es decir, un factor de potencia en retraso puro.
circuito serie RL
Como sabemos, todas las bobinas tienen cierto grado de resistencia del devanado junto con inductancia, por lo que no existe un circuito físico de inductancia pura. En tal circuito, la resistencia se considera un elemento en serie con el inductor.
Considere el siguiente diagrama donde una resistencia pura está conectada en serie con una inductancia pura. Esta combinación en serie está conectada a través de una fuente de alimentación de CA con voltaje v = V.metros Pecado ωt.
En la serie Rl En el circuito, el voltaje a través del inductor está desfasado tanto con la corriente que fluye a través del circuito como con el voltaje a través de la resistencia, como se muestra en el diagrama anterior. El voltaje inducido en el inductor resiste el flujo de corriente, por lo que Vl La corriente I avanza y cae a través de la resistencia VR por 900.
Sean I y V las corrientes que circulan por el circuito.l y VR son la caída de voltaje a través de la inductancia y la resistencia, respectivamente.
Voltaje a través de la resistencia, VR = yoR
Voltaje a través del inductor, Vl = I × XL (donde XL = 2πfL)
Desde el fáser anterior,
V = √ (VR2 +Vl2) = √ (IR)2+ (IXL)2)
= yo √ (R2 +XL2) = yoz
donde Z es la impedancia de Rl Es un circuito en serie, y √ (R2 +XL2).
triángulo de impedancia
La resistencia que ofrece un circuito de CA al flujo de corriente sinusoidal se llama impedancia. También se puede definir como la relación entre tensión y corriente sinusoidales. Se denota con la letra Z y se mide en ohmios.
Del diagrama fasorial de la serie RL,
Tan ϕ = Vl /VR =XL/R
cosϕ = VR /V = R/Z
pecado ϕ = Vl / V = XL / Z
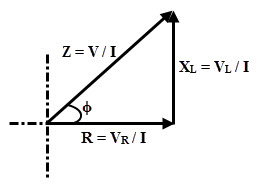
Si tenemos todos los lados del triángulo obtenido porl Al dividir un circuito en serie por la corriente se obtiene una impedancia triangular como se muestra. R,X de este triángulol La componente Z se puede expresar como:
R = Z porque ϕ
XL = Z sen ϕ
Z = √ (R2 +XL2)
y ϕ = Tan-1 (XL/R)
ejemplo
Encuentre la ecuación para la corriente y también calcule la potencia en el circuito en serie RL con R = 50 ohmios y L = 0.159 H excitado con un voltaje de v = 283 sen 100πt.
Reactancia inductiva, XL = 2πfL = 100π × 0,159
= 49,95 ohmios
Z = R + jXL = 50 + j49,95
La conversión a forma polar da Z = 70,675 ∠44,97 ohmios.
Corriente, i = v/ Z = (283 sen (100πt – 44,97))/ 70,675
i = 4 sen (100πt – π/4) A
P = VI cosθ
= (283/√2) (4/√2) cos 44,97
= 400,43A