circuito capacitivo de ca

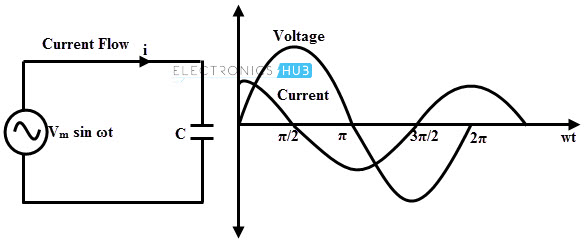
Un condensador se forma siempre que dos placas conductoras están separadas por un medio dieléctrico o aislante. La propiedad básica de un condensador es que almacena carga eléctrica. Si se conecta una fuente de voltaje a través del capacitor, las dos placas adquieren cargas opuestas. Es decir, una placa almacena una carga positiva y la otra placa almacena una carga negativa.

[adsense1]

Esto hace que los electrones fluyan de una placa a la otra hasta que el voltaje a través del capacitor sea igual al voltaje aplicado. La tasa de cambio del voltaje a través del capacitor determina la corriente que fluye a través del capacitor.

Los condensadores, junto con resistencias e inductores, ayudan a construir circuitos de CA muy complejos en muchas aplicaciones electrónicas. Esta sección explica brevemente el funcionamiento de los circuitos de CA que utilizan capacitancia.

Aplicar corriente alterna a un condensador puro.

Cuando un condensador puro se conecta a una fuente de alimentación de CA, el condensador alterna entre carga y descarga a medida que cambia el valor del voltaje aplicado. La carga que fluye a través de un capacitor es proporcional a la capacitancia (el tamaño del capacitor) y al voltaje aplicado a través del capacitor.se puede expresar como

Q = reanudar

V=Q/C

dónde

V = voltaje aplicado (voltios)

Q = carga del condensador (en culombios)

C = Capacitancia del condensador (Faradios)

[adsense2]

Considere el circuito anterior con un capacitor puro conectado a través de una fuente de voltaje de CA con v = Vm sen ωt. Una fuente de voltaje hace que la corriente fluya a través de un circuito. La corriente es proporcional a la tasa de cambio de carga en el capacitor a lo largo del tiempo.

Corriente en el circuito, i = d(q)/dt

Sustituyendo q = C v = C Vm sin ωt en la ecuación anterior se obtiene lo siguiente.

yo = d/dt (CV_metros pecado ωt) = ωC V_metros costo

o yo = ω CV_metros pecado (ωt + π/2)

Cuando el término pecado (ωt + π/2) es 1, el valor actual es máximo.

I_metros = ωC Vm

Sustituir este valor actual da como resultado:

yo = yo_metros pecado (ωt + π/2)

De la ecuación anterior, queda claro que en un circuito puramente capacitivo, la corriente se adelanta al voltaje en 900 grados. Esto significa que si se conecta un condensador puro a través de una fuente de alimentación de CA, la corriente máxima fluirá a través del condensador cuando cambie la tasa de cambio de voltaje. es el máximo (posición de voltaje cero). Y esta corriente disminuye cuando la tasa de cambio de voltaje es mínima.

En otras palabras, el estado de descarga del capacitor hace que la corriente máxima fluya a través del circuito cuando el voltaje a través del capacitor comienza a aumentar.

Una vez que el condensador está completamente cargado a su voltaje máximo, la corriente de carga cae a cero. Cuando el voltaje comienza a caer, el capacitor comienza a cargarse. Por lo tanto, la relación entre voltaje y corriente se puede describir como un desfase de 90 grados.

Por lo tanto, la corriente del capacitor se adelanta 90 grados al voltaje aplicado. A continuación se muestra el diagrama fasorial de un circuito capacitivo de CA.

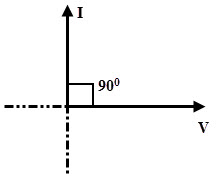
reactancia capacitiva

De la derivación anterior, la ecuación de corriente máxima queda como:

I_metros = ωCV_metros

V_metros / I_metros = (1/wC)

Esta relación de voltaje y corriente es la opuesta al flujo de corriente por un circuito capacitivo. Esta cantidad (1/w C) se llama reactancia capacitiva y se expresa como XC medida en ohmios.

La reactancia capacitiva de un circuito de CA se puede expresar como:

XC = (1 / ω C) = (1 / 2πf C) (porque ω = 2Πf)

dónde

XC es la reactancia capacitiva en ohmios.

f es la frecuencia de la tensión de alimentación

C es la capacitancia del condensador (faradios)

De la ecuación anterior, la reactancia capacitiva de un capacitor en un circuito de CA es función de la frecuencia y la capacitancia. La reactancia capacitiva disminuye a medida que aumenta la frecuencia, lo que resulta en un aumento en la corriente que fluye a través del circuito.

De manera similar, a medida que disminuye la frecuencia, aumenta la reactancia, lo que resulta en una disminución de la corriente. La relación entre la reactancia capacitiva y la frecuencia se muestra en la siguiente figura.

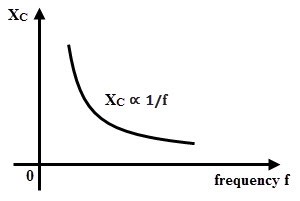
Potencia y factor de potencia en circuitos de CA capacitivos.

La potencia en un circuito de CA es el producto del voltaje y la corriente instantáneos.Esto se da como

P = v × yo

P = V_metros pecado ωt×I_metros pecado(ωt+90)

Integración a lo largo del ciclo

P = V_metros pecado ωt×I_metros pecado(ωt+90)

P = 1/2π (∫⁰_2π V_metros pecado ωt×I_metros pecado (ωt + 90) dwt)

= (V_metros I_metros / 2π) (∫⁰_2π sen ωt cos ωt dwt)

= (V_metros I_metros / 4π) (∫⁰_2π (pecado 2 ωt)/2 dwt)

= (V_metros I_metros/ 8π) (-cos 4π + cos 0)

= (V_metros I_metros / 8π) (-1 + 1)

p=0

Por lo tanto, al igual que en los circuitos inductivos, la potencia absorbida en capacitancia pura es cero como potencia absorbida y devuelta durante cada medio ciclo. La siguiente figura muestra las formas de onda de voltaje, corriente y potencia para un circuito capacitivo de CA.

Durante el semiciclo positivo de la forma de onda de potencia, la energía se almacena en el condensador durante la carga. Y durante el semiciclo negativo, la energía almacenada regresa a la fuente durante la descarga. Sabemos que la potencia media absorbida por el circuito es cero ya que el área de ambos ciclos es igual.

En este circuito puramente capacitivo, hay una diferencia de fase (conductor) de 900° entre las formas de onda de voltaje y corriente. Entonces el factor de potencia se convierte en:

Factor de potencia, cosθ = cos 90⁰ = 0

Por lo tanto, el factor de potencia de un circuito puramente capacitivo es de adelanto cero o factor de potencia de adelanto puro.

circuito serie RC

Este tipo de circuito es similar a R._l Es un circuito en serie, pero se utiliza un condensador en lugar de un inductor. En el siguiente diagrama, se conecta una disposición en serie de resistencias y condensadores a través de una fuente de alimentación de CA.

Como se muestra en el siguiente diagrama, la caída de voltaje a través de la resistencia está en fase con la corriente, pero la corriente adelanta la caída de voltaje a través del capacitor en 900 grados.

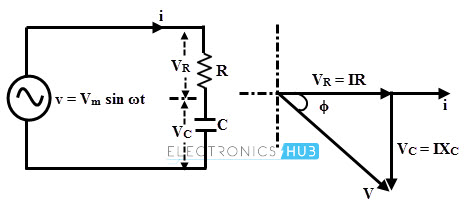
Caída de voltaje a través de la resistencia, VR = IR

Voltaje a través de un capacitor puro, VC = I ×X_C (donde X_C = 1/2πfC)

Por lo tanto, V = √ (V_R² +V_C²) = √ (IR)² +(IX_C)²)

= yo √ (R 2 + X_C 2) = IZ

donde Z es la impedancia del circuito en serie RC y √ (R ² +X_C²).

triángulo de impedancia

Del diagrama fasorial de la serie RC,

Tan ϕ = V_C/V_C =X_C /R

cosϕ = V_C/V = R/Z

pecado ϕ = V_C /V=X_C /Z

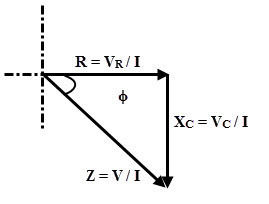
A partir del triángulo de impedancia, R, XC y la impedancia total del circuito en serie RC se pueden expresar como:

R = Z porque ϕ

X_C= Z sen ϕ

Z = √ (R ² +X_C²)

y ϕ = bronceado^-1 (-X_C /R)

circuito serie RLC

En este circuito, se conecta una conexión en serie de una resistencia, un inductor y un condensador a través de una fuente de alimentación de CA. Dependiendo del valor obtenido de la combinación de reactancia capacitiva e inductiva, el circuito funciona como circuito RL o circuito RC. Restar la reactancia mayor de la reactancia menor da la reactancia total.

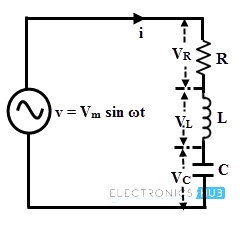
Voltaje a través de la resistencia, V_R = yo_R

Voltaje a través del inductor, V_l = IX_l

Voltaje a través de un capacitor puro, V_C= IX_C

El diagrama fasorial de este circuito depende del valor de X._l y X_Cconsideremos diferentes valores de estas reactancias.

(1)×_l > ×_C

En el caso de X_l > ×_Centonces V_l (=IX_l) es mayor que VC (= IX)_C). Por tanto, el circuito tiene propiedades inductivas como resultado de V._ly V_C Dirigido a VL. Por tanto, el circuito se comporta como un circuito en serie RL.

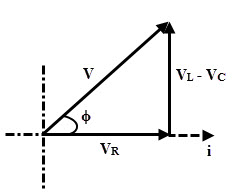
Por lo tanto, la tensión de alimentación, V = √ ((V_R² + (V_l –V_C)²) = √ ((yo_R)₂ +(IX_l– IX_C)₂)

V = yo √ ((R)² +(X_l-X_C) ²)

V = IZ

Aquí, Z = √ ((R)² +(X_l– X_C)²)

(2) ×_l C

En el caso de X_l C o XC >X_l Entonces V._l (=IX_l) es menor que VC (= IX)_C). Por lo tanto, el circuito se vuelve de naturaleza capacitiva como resultado de V._l y V_C dirigido hacia V_C. Por tanto, el circuito se comporta como un circuito en serie RC.

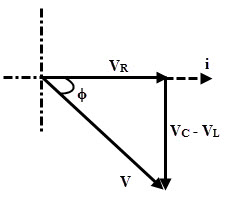
Por lo tanto, la tensión de alimentación, V = √ ((V²_R + (V_C –V_l)²) = √ ((IR)²+(IX_C– IX_l)²)

V = yo √ ((R)² +(X_C-X_l)²)

V = IZ

Aquí, Z = √ ((R)² +(X_l– X_C)²)

(3) ×_l =X_C

En el caso de X_l =X_Centonces V_l=v_C. En tal caso, el voltaje resultante será cero. Por lo tanto, V._R = V. Por tanto, el circuito se comporta como un circuito resistivo.

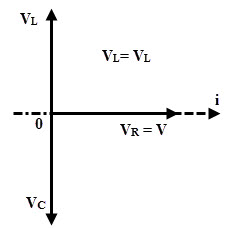
Crea un diagrama fasor,

V = V_R

V = IR

V = IZ

Aquí, Z = R.

ejemplo

Un voltaje sinusoidal de CA monofásico de v = 283 sen 314t se conecta a través de un capacitor puro de 100 µF. Luego, encuentre la corriente que fluye a través del capacitor.

Al convertir el voltaje del dominio del tiempo a la forma polar se obtiene:

v = 283 sen 314t = 283∠0⁰

La reactancia capacitiva se puede determinar como:

X_C = (1 /jw C) = (1 / 314 × 100μ) = 31,8 ∠– 90⁰

Según la ley de Ohm, la corriente que circula en un circuito se calcula de la siguiente manera.

Ic = (V/j

Ic = (283∠0)⁰ /31,8∠–90⁰)

Ic = 8,8 ∠+90⁰)