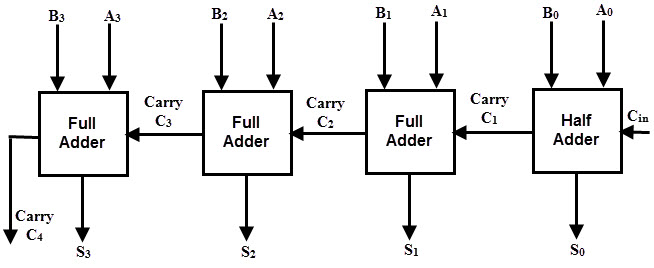
Para los sumadores paralelos, la suma binaria de dos números comienza cuando todos los bits del sumando y del sumando deben estar disponibles al mismo tiempo para realizar el cálculo. En los circuitos sumadores en paralelo, la salida de acarreo de cada etapa del sumador completo está conectada a la entrada de acarreo de la siguiente etapa superior, por lo que también se le llama sumador de acarreo ondulado.
[adsense1]
En un circuito sumador de este tipo, ninguna etapa puede producir una suma y transportar una salida hasta que se produzca un acarreo de entrada. Por lo tanto, el proceso de suma introduce un retraso de tiempo significativo conocido como retraso de propagación de acarreo. En cualquier circuito combinacional, una señal debe propagarse a través de las puertas antes de que la suma de salida correcta esté disponible en los terminales de salida.
Considere el diagrama de arriba. Tan pronto como se introduce la señal de entrada, el sumador completo correspondiente genera la suma S4. Sin embargo, la entrada de acarreo C4 no está disponible en su valor final de estado estable hasta que el acarreo c3 esté disponible en su valor de estado estable. De manera similar, C3 depende de C2 y C2 depende de C1. Por lo tanto, para que la salida S4 y el acarreo C5 establezcan sus valores finales de estado estable, el acarreo debe propagarse a todas las etapas.
El tiempo de propagación es igual al retardo típico de propagación de la puerta multiplicado por el número de niveles de puerta en el circuito. Por ejemplo, si el retardo de propagación de cada etapa sumadora completa es de 20 n segundos, S4 alcanza su valor final correcto después de 80 n (20 × 4) segundos. Ampliar el número de etapas para agregar más bits empeora aún más esta situación.
Por lo tanto, el número de bits agregados por un sumador paralelo depende del tiempo de propagación del acarreo. Sin embargo, la señal debe propagarse a través de la puerta durante un período de tiempo suficiente para producir la salida correcta o deseada.
Aquí se explica cómo acelerar un sumador paralelo que realiza suma binaria.
- Los retrasos en la propagación se pueden reducir empleando puertas más rápidas con retrasos reducidos. Sin embargo, todas las puertas lógicas físicas tienen limitaciones de capacidad.
- Otro método consiste en aumentar la complejidad del circuito para reducir el tiempo de retardo de acarreo. Hay varios métodos disponibles para acelerar los sumadores paralelos, pero un método comúnmente utilizado emplea el principio de la suma de acarreo anticipado eliminando la lógica de acarreo entre etapas.
Volver a la cima
[adsense2]
Llevar sumador anticipado
Los sumadores de anticipación son sumadores paralelos más rápidos que reducen el retraso de propagación debido a un hardware más complejo, por lo que cuestan más. Este diseño reduce la lógica de acarreo para un grupo fijo de bits en el sumador a dos niveles de lógica. Esto no es más que una variación del diseño de transporte ondulado.
Este método utiliza puertas lógicas para examinar los bits de orden inferior del sumando y del apéndice para ver si se produce un acarreo de orden alto. Analicemos en detalle.
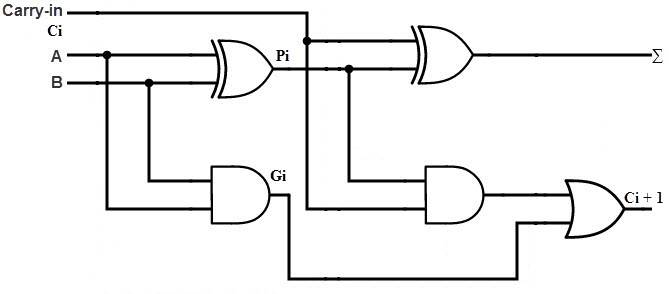
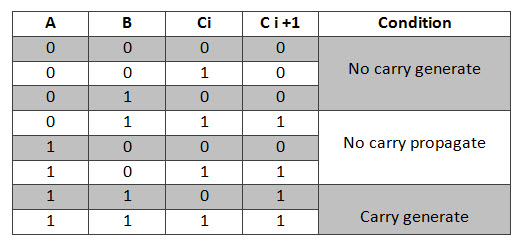
Considere el circuito sumador completo que se muestra arriba junto con la tabla de verdad correspondiente. Al definir dos variables como generación de acarreo Gi y propagación de acarreo Pi, obtenemos:
PAGI =UnI ⊕BI
Gi Aibi
La salida suma y la salida de acarreo se pueden expresar como:
Si = Pi ⊕ Ci
Ci +1 = Gi + Pi Ci
Aquí, Gi es una generación de acarreo que genera un acarreo cuando Ai y Bi son ambos 1, independientemente del acarreo de entrada. Pi es una propagación de acarreo y está asociada con la propagación de un acarreo de Ci a Ci+1.
La función booleana de salida de acarreo de cada etapa de un sumador anticipado de acarreo de cuatro etapas se puede expresar como:
C1 = G0 + P0 Cin
C2 = G1 + P1 C1
= G1 + P1 G0 + P1 P0 Cin
C3 = G2 + P2 C2
= G2 + P2 G1+ P2 P1 G0 + P2 P1 P0 Cin
C4 = G3 + P3 C3
= G3 + P3 G2+ P3 P2 G1 + P3 P2 P1 G0 + P3 P2 P1 P0 Cin
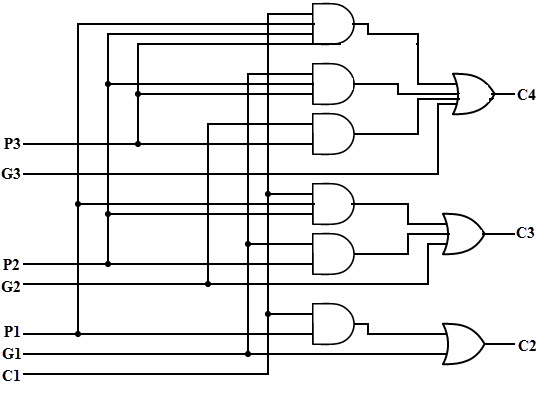
De la ecuación booleana anterior, podemos ver que C4 no necesita esperar a que C3 y C2 se propaguen; de hecho, C4 se propaga simultáneamente con C3 y C2. Dado que la expresión booleana para cada salida de acarreo es una suma de productos, se pueden implementar con una puerta AND de un nivel seguida de una puerta OR.
La siguiente figura muestra la implementación de tres funciones booleanas para cada salida de acarreo (C2, C3 y C4) del generador de acarreo.
Por lo tanto, se puede implementar un sumador paralelo de 4 bits con un esquema de acarreo para acelerar la suma binaria, como se muestra en la siguiente figura. En este caso, cada salida suma requiere dos puertas Ex-OR. La primera puerta Ex-OR produce una salida variable Pi y la puerta AND produce una variable Gi.
Entonces todos estos P y G se generan en dos niveles de puerta. El generador de arrastre permite que todas estas señales P y G se propaguen después de que se establezcan en sus valores de estado estable, produciendo portadoras de salida con un retardo de dos niveles en la puerta. Por tanto, los tiempos de retardo de propagación de las salidas sumarias S2 a S4 son iguales.
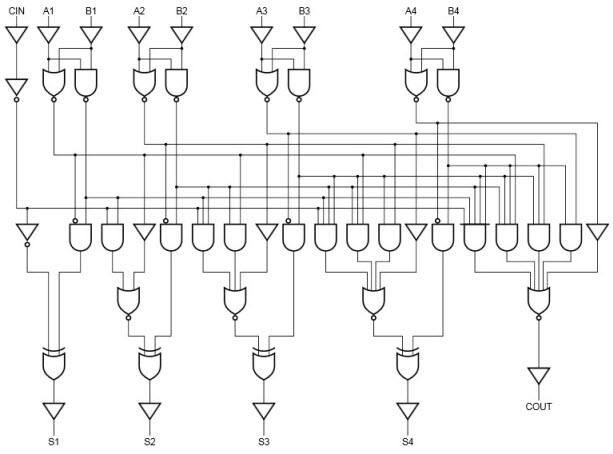
También es posible construir sumadores paralelos de 16 y 32 bits conectando en cascada varios sumadores de 4 bits utilizando lógica de acarreo. Un sumador de anticipación de acarreo de 16 bits se construye conectando en cascada cuatro sumadores de 4 bits con dos retardos de puerta adicionales, mientras que un sumador de anticipación de acarreo de 32 bits se construye conectando en cascada dos sumadores de 16 bits.
El sumador de acarreo de 16 bits requiere 5 retrasos de puerta y 8 retrasos de puerta para obtener C16 y S15, respectivamente, en comparación con 9 retrasos de puerta cada uno para C16 y S15 en el bloque sumador de acarreo de 4 bits en cascada. Los retrasos son pequeños en comparación entre sí. De manera similar, un sumador de 32 bits requiere retrasos de 7 y 10 puertas en C32 y S31, pero si el sumador de 32 bits se implementa con ocho sumadores de 4 bits, los retrasos de 18 y 17 puertas para la misma salida serán menores en comparación.
Volver a la cima
Llevar IC sumador anticipado
Varios fabricantes integran sumadores de anticipación de transporte rápido en circuitos integrados con diferentes configuraciones de bits. Se encuentran disponibles varios circuitos integrados generadores de acarreo separados porque deben conectarse a puertas lógicas para realizar operaciones de suma.
Un IC generador de anticipación de acarreo típico es el 74182, que tiene cuatro pares de señales activas de propagación de acarreo bajo (como P0, P1, P2 y P3), generación de acarreo (Go, G1, G2 y G3) y una entrada alta activa. (Cn).
Proporciona portadoras altas activas (Cn+x, Cn+y, Cn+z) en cuatro grupos de sumadores binarios. El IC también facilita la lectura anticipada de otros niveles con salidas activas de propagación baja y generación de acarreo.
Las expresiones lógicas proporcionadas por IC 74182 son:
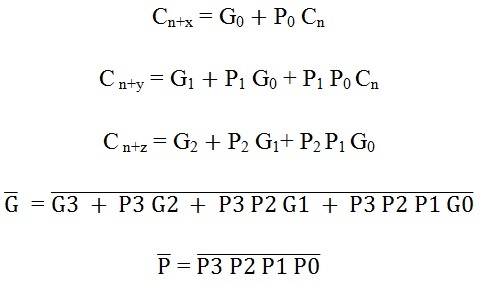
Por otro lado, existen muchos circuitos integrados sumadores de alta velocidad que combinan una serie de sumadores completos con un circuito de acarreo. La forma más común de dicho IC es 74LS83/74S283. Se trata de un circuito integrado de sumador paralelo de alta velocidad de 4 bits que contiene cuatro sumadores completos interconectados con circuitos de acarreo.
El símbolo funcional de este tipo de IC se muestra en la siguiente figura. Acepte dos números de 4 bits como A3A2A1A0 y B3B2B1B0 e ingrese Cin0 en la posición LSB. Este IC produce el bit de suma de salida como S3S2S1S0 y una salida de acarreo Cout3 en la posición MSB.
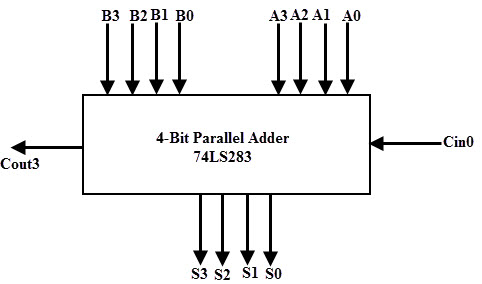
Al conectar en cascada dos o más circuitos integrados sumadores paralelos, puede realizar adiciones binarias más grandes, como adiciones de 8, 24 y 32 bits.
Volver a la cima