Los sistemas digitales requieren comparaciones de datos al realizar operaciones aritméticas o lógicas. Esta comparación determina si un número es mayor, igual o menor que el otro número. Los comparadores digitales se utilizan ampliamente en sistemas combinacionales y están diseñados específicamente para comparar las magnitudes relativas de números binarios.
También están disponibles en forma de IC con varias configuraciones de comparación de bits, como 4 bits, 8 bits, etc. También puede conectar varios comparadores en una disposición en cascada para comparar números en longitudes más largas. Para dos números binarios, primero se deben comparar los bits más significativos.
Si estos MSB son iguales, sólo necesita comparar el siguiente bit significativo. Sin embargo, si los MSB no son iguales, está claro que A es mayor o menor que B y el proceso de comparación finaliza.
Por ejemplo, dos números de 2 bits son A = A1A0 y B=B1B0. Si A1 no es igual a B1, está claro que A es mayor que B si A1 =1 y B1= 0, o A es menor que B si A0= 0 y B0 =1. En esta etapa finaliza el proceso de comparación.
Si los MSB son iguales, es decir, solo A1=B1, entonces necesitamos comparar los siguientes bits significativos, A0 y B0, para determinar si los números son mayores, menores o iguales. Por lo tanto, el comparador produce tres resultados porque L, E y G corresponden a comparaciones menores que, iguales y mayores que.
Hay dos tipos de comparadores digitales
comparador de identidad
Un comparador que tiene un solo terminal de salida y produce una salida baja o alta es un comparador de identidad.
comparador de magnitud
Un comparador con tres terminales de salida que verifica tres condiciones (mayor o igual, menor o igual). Comparador de magnitud.
Volver a la cima
Tabla de contenido
comparador digital
Un comparador digital de magnitud compara dos números digitales o binarios (piense en A y B) y calcula su valor relativo para ver si un número es igual, menor o mayor que el otro número digital. Este es un circuito combinacional que determina el tamaño de el circuito.
Usando tres variables binarias, el resultado de la comparación es A>B, A
Estos comparadores pueden comparar números de 2, 4 y 8 bits según los requisitos de la aplicación. Estos están disponibles en circuitos integrados de la familia lógica TTL y CMOS, algunos de estos circuitos integrados son el IC 7485 (comparador de 4 bits), el IC 4585 (comparador de 4 bits en la familia CMOS) y el IC 74AS885 (comparador de 8 bits).
Volver a la cima
Comparador de magnitud de un solo bit
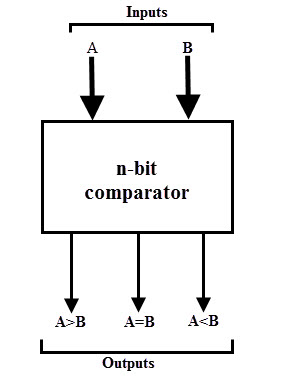
Un comparador que se utiliza para comparar dos números de 2 bits, es decir, 1 bit, se denomina comparador de un solo bit. Consta de dos entradas que permiten dos números de un solo bit y tres salidas que producen salidas de comparación menores, iguales y mayores que.
La siguiente figura muestra el diagrama de bloques de un comparador de magnitud de un solo bit. Este comparador compara dos bits y calcula L (A
A continuación se muestra la tabla de verdad para un comparador de un solo bit. Si A0 B0 = 00 y 11, entonces la salida A=B será Alta ya que ambas entradas son iguales. Si A0 B0 = 01, B es mayor que A, entonces AB está activo.
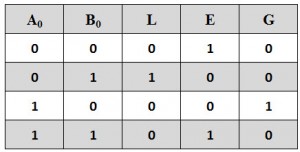
De la tabla de verdad, la expresión lógica para cada resultado se puede expresar como:
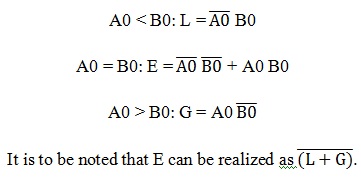
Usando estas expresiones booleanas, podemos implementar el circuito lógico para este comparador usando dos puertas AND, una puerta NOT y una puerta Ex-NOR, como se muestra en la siguiente figura. La puerta AND se utiliza para detectar si un número binario es menor o mayor que otro bit, y la puerta Ex-NOR se utiliza para detectar si dos números binarios son iguales.
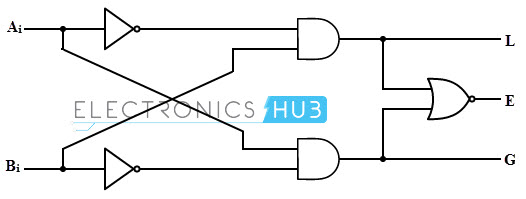
En el diagrama, la entrada de una puerta AND es A0 (B0) ̅ y la entrada de la otra puerta AND es (A0) ̅ B0. Por lo tanto, una salida de la puerta AND será 1 si A0 > B0 (es decir, A0 =1 y B0 =0) y 0 si A0 < B0 (es decir, A0 =0 y B0 =1). De manera similar, la otra salida de la puerta AND es A0. < B0 (つまり、A0 =0 および B0 =1) の場合は 1 になり、A0 > Es 0 si B0 (es decir, A0 =1 y B0 =0).
La puerta Ex-NOR tiene entradas A0 B0, por lo que si A0 = B0, la salida de la puerta Ex-NOR será 1, y si A0 no es igual a B0, la salida será 0.
Volver a la cima
comparador de 2 bits
Un comparador de 2 bits compara dos números binarios de 2 bits cada uno y produce una relación, como por ejemplo si un número es igual, mayor o menor que el otro número. La siguiente figura muestra un diagrama de bloques de un comparador de 2 bits con cuatro entradas y tres salidas.
El primer número A se especifica como A = A1A0 y el segundo número se especifica como B = B1B0. Este comparador tiene G (G = 1 si A>B), E (E = 1 si A = B) y L (A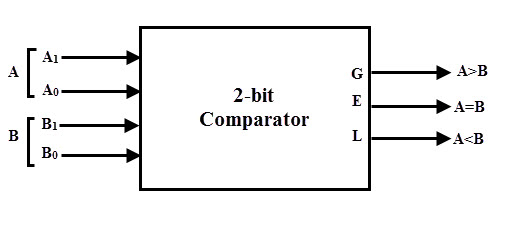
La tabla de verdad para este comparador se muestra a continuación. Se muestran varios estados de entrada y salida.
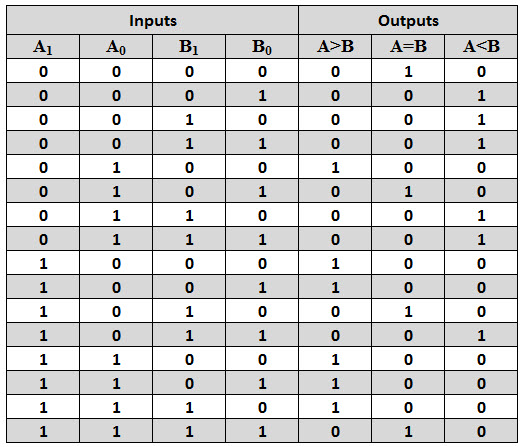
La simplificación k-map de la tabla de verdad anterior es:
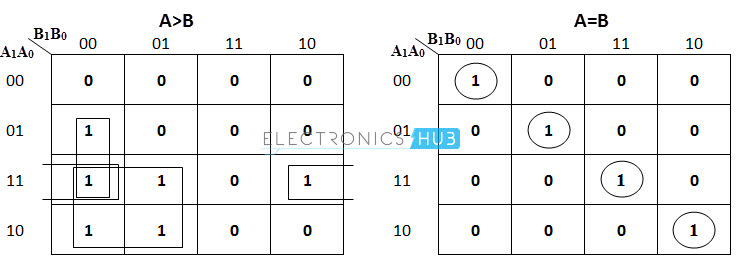
A partir de la simplificación de k-map anterior, cada resultado se puede expresar como:
Al utilizar las ecuaciones booleanas obtenidas anteriormente para cada salida, podemos implementar un diagrama lógico usando 4 puertas NOT, 7 puertas AND, 2 puertas OR y 2 puertas Ex-NOR.
La siguiente figura muestra el diagrama lógico de un comparador de 2 bits que utiliza puertas lógicas básicas. Este comparador también se puede configurar conectando en cascada dos comparadores de 1 bit.
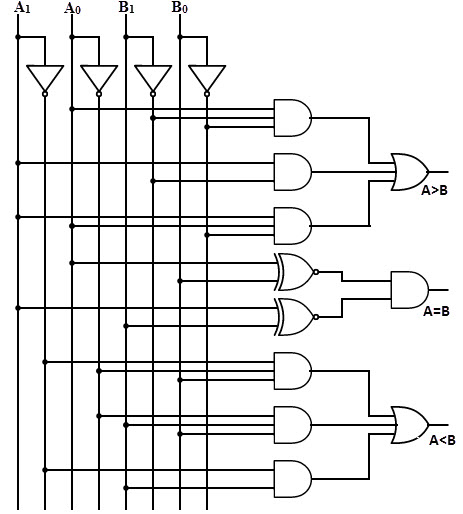Volver a la cima
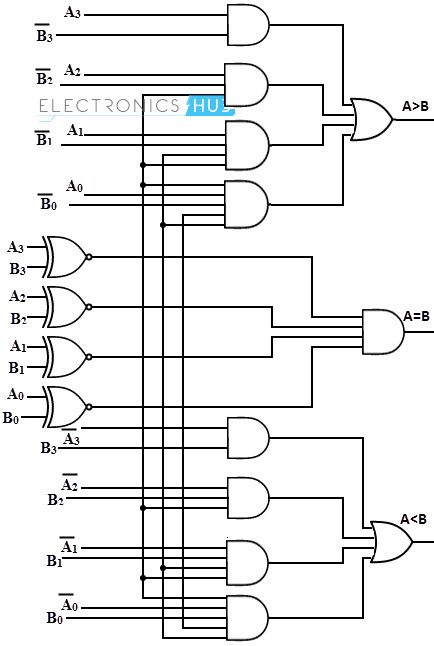
comparador de 4 bits
Se puede utilizar para comparar dos palabras de 4 bits. Los dos números de 4 bits son A = A3 A2 A1 A0 y B3 B2 B1 B0. Aquí A3 y B3 son los bits más significativos.
Compara cada uno de estos bits de un número con los bits del otro número, A = B, A < B、および A>Producir una de las salidas de B. La declaración lógica de salida para este convertidor es:
- Si A3 = 1 y B3 = 0, A es mayor que B (A>B).o
- Si A3 y B3 son iguales y A2 = 1 y B2 = 0, entonces A > B o
- Si A3 y B3 son iguales y A2 y B2 son iguales, entonces A>B si A1 = 1 y B1 = 0.o
- Si A3 y B3 son iguales, A2 y B2 son iguales, A1 y B1 son iguales, A0 = 1 y B0 = 0, entonces A > B.
De la declaración anterior, la expresión lógica de salida A > B se puede escribir como:
Se produce una salida igual cuando cada bit individual de un número coincide exactamente con el bit correspondiente de otro número. En este caso, la expresión lógica para la salida A=B se puede escribir como:
E = (A3 Ex-NOR B3) (A2 Ex-NOR B2) (A1 Ex-NOR B1) (A0 Ex-NOR B0)
A partir de la fórmula booleana de salida anterior, el circuito lógico para este comparador se puede implementar utilizando las puertas lógicas que se muestran a continuación. En este ejemplo, las cuatro salidas de la puerta Ex-NOR se aplican a una puerta AND, dando una variable binaria E o A = B. Las otras dos salidas también utilizan la salida Ex-NOR para producir la función booleana que se muestra en la figura.
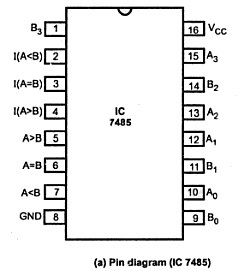
Los comparadores de 4 bits están disponibles principalmente en forma de IC, y un tipo común de este IC es el 7485. Este IC tiene I (A>B), I (A
Además de un comparador normal, este IC tiene una entrada en cascada para facilitar la conexión en cascada de múltiples comparadores. Al conectar en cascada varios de estos CI comparadores, se puede comparar cualquier número de bits.
Volver a la cima
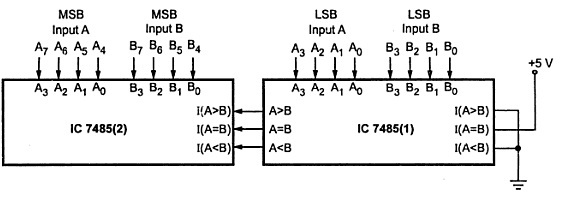
comparador de 8 bits
Un comparador de 8 bits compara dos números de 8 bits conectando en cascada dos comparadores de 4 bits. Las conexiones del circuito para este comparador se muestran a continuación, con A del comparador inferior
Para el comparador inferior, la entrada en cascada A=B debe conectarse a Alta y las otras dos entradas en cascada A, B deben conectarse a BAJA. La salida del comparador superior se convierte en la salida de este comparador de 8 bits.
Volver a la cima
Ejemplo de aplicación de comparador
- Estos son circuitos de decodificación de direcciones en computadoras y dispositivos basados en microprocesadores que se utilizan para seleccionar dispositivos de entrada y salida específicos para almacenar datos.
- Se utilizan en aplicaciones de control donde se comparan números binarios que representan variables físicas como temperatura, posición, etc. con un valor de referencia. La salida del comparador se utiliza luego para accionar el actuador y acercar la variable física al punto de ajuste o valor de referencia.
- controlador de proceso
- control de servomotor
Volver a la cima