Gran parte de la comunicación moderna es de naturaleza digital, una combinación de unos y ceros. Los datos digitales se transmiten por cables (para comunicaciones por cable) o de forma inalámbrica. Incluso en modos de comunicación avanzados, pueden ocurrir errores (debido al ruido) durante la transmisión de datos.
El error más simple es un bit roto. Es decir, un 1 se puede enviar como 0 y viceversa. Para garantizar que los datos recibidos sean los previstos, el receptor debe poder detectar errores.
En este tutorial, aprenderá sobre bits de paridad, paridad par, paridad impar, generadores de paridad y verificadores de paridad utilizando ejemplos y circuitos del mundo real.
Tabla de contenido
¿Qué es un bit de paridad?
La tecnología de generación de paridad es una de las técnicas de detección de errores más utilizadas para la transmisión de datos. En los sistemas digitales, a medida que se transmiten y procesan datos binarios, los datos pueden verse afectados por el ruido que cambia los 0 (de bits de datos) a 1 o los 1 a 0. Existe una posibilidad.
Por lo tanto, se agrega un bit de paridad a la palabra que contiene los datos para que el número de unos sea par o impar. Un mensaje que contiene bits de datos y bits de paridad se envía desde el transmisor al receptor.
En el lado receptor se cuenta el número de unos en el mensaje y si no coincide con lo enviado, significa que hay un error en los datos. Por tanto, el bit de paridad se utiliza para detectar errores durante la transmisión de datos binarios.
Generador de paridad y verificador de paridad
Un generador de paridad es un circuito lógico combinacional que genera bits de paridad en el transmisor. Por otro lado, el circuito que verifica la paridad dentro del receptor se llama verificador de paridad. Los sistemas digitales suelen utilizar circuitos o dispositivos que combinan generadores de paridad y verificadores de paridad para detectar errores de un solo bit en los datos transmitidos.
Paridad par y paridad impar
La suma de bits de datos y bits de paridad puede ser par o impar. En paridad par, el bit de paridad agregado hace que el número total de unos sea par, mientras que en paridad impar, el bit de paridad agregado hace que el número total de unos sea impar.
El principio básico involucrado en la implementación de un circuito de paridad es que la suma de un número impar de unos siempre suma 1, y la suma de un número par de unos siempre suma 0. La detección y corrección de dichos errores se puede implementar utilizando puertas Ex-OR. Una puerta OR tiene una salida de cero si el número de entradas es par).
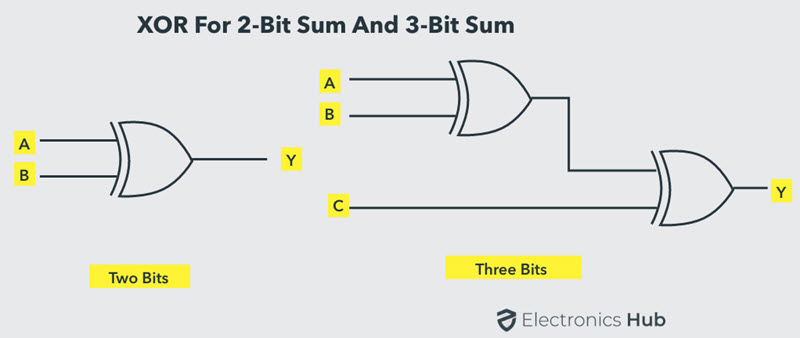
Para generar una suma de 2 bits, una puerta Ex-OR es suficiente, pero para sumar 3 bits, se requieren dos puertas Ex-OR, como se muestra en la siguiente figura.
generador de paridad
Este es un circuito combinacional que acepta n-1 bits de datos y genera bits adicionales que se envían junto con el flujo de bits. Este bit adicional o especial se llama bit de paridad.
En el esquema de bits de paridad par, si hay un número par de unos en el flujo de datos, el bit de paridad es ‘0’, y si hay un número impar de unos en el flujo de datos, el bit de paridad es ‘1’.
En el esquema de bits de paridad impar, si hay un número par de unos en el flujo de datos, el bit de paridad es ‘1’, y si hay un número impar de unos en el flujo de datos, el bit de paridad es ‘0’. Se analizan tanto los generadores de paridad pares como los impares.
incluso generador de paridad
Supongamos que se envía un mensaje de 3 bits con bits de paridad pares. Supongamos que se aplican tres entradas A, B y C al circuito y el bit de salida es el bit de paridad P. Para producir un bit de paridad par P, el número total de unos debe ser par.
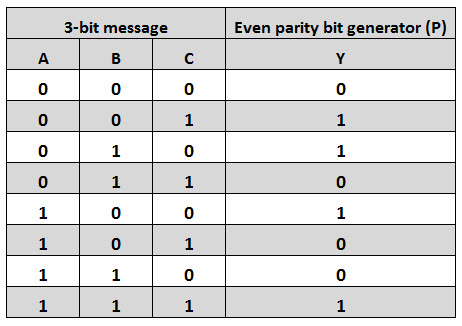
La siguiente figura muestra la tabla de verdad de un generador de paridad par, y cuando el número de unos en la tabla de verdad es impar, se coloca un 1 como bit de paridad para que todos los unos sean pares.
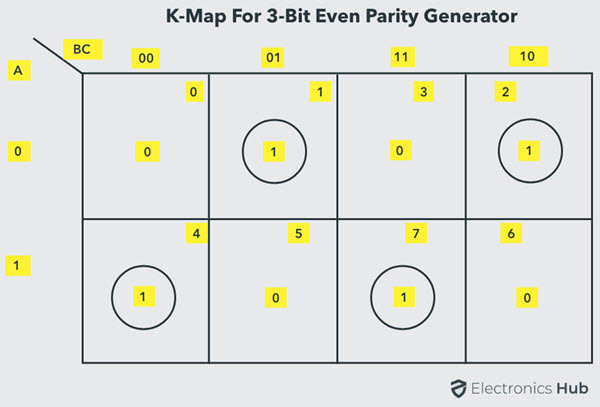
La simplificación de K-map para el generador de paridad par de mensajes de 3 bits es:
De la tabla de verdad anterior, la expresión simplificada para el bit de paridad se puede escribir como:
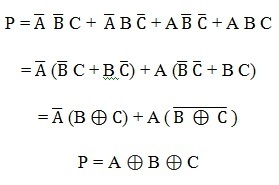
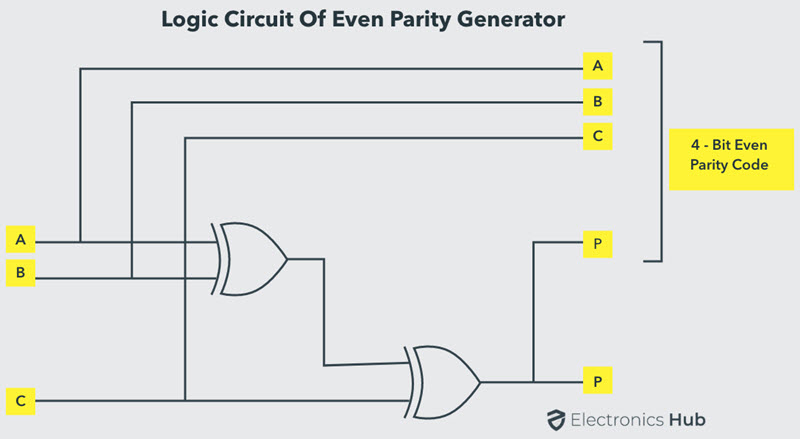
La ecuación anterior se puede implementar utilizando dos puertas Ex-OR. A continuación se muestra el diagrama lógico de un generador de paridad par con dos puertas Ex – OR. El mensaje de 3 bits con paridad generado por este circuito se envía al receptor y se verifica la presencia de errores mediante un circuito verificador de paridad.
Para generar bits de paridad pares para datos de 4 bits, se requieren tres puertas Ex-OR para sumar los 4 bits, y la suma es el bit de paridad.
generador de paridad impar
Considere 3 bits de datos transmitidos con un número impar de bits de paridad. Las tres entradas son A, B y C, y P es el bit de paridad de salida. Para producir bits de paridad impares, el número total de bits debe ser impar.
En la siguiente tabla de verdad, se coloca un 1 en el bit de paridad para hacer que el número total de bits sea impar si el número total de unos en la tabla de verdad es par.
La tabla de verdad para un generador de paridad impar se puede simplificar utilizando un mapa K de la siguiente manera:
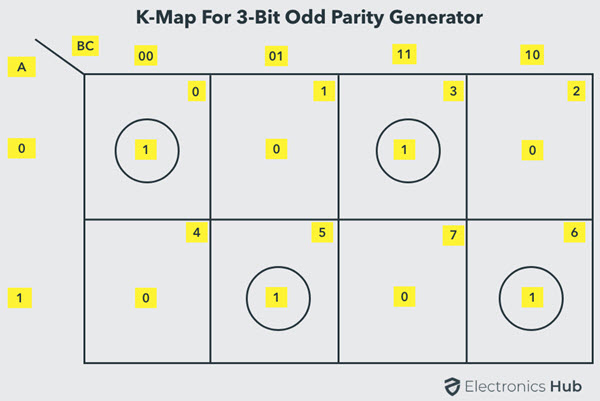
La expresión del bit de paridad de salida de este generador se obtiene de la siguiente manera.
P = A ⊕ (B ⊕ C)
La expresión booleana anterior se puede implementar utilizando una puerta Ex-OR y una puerta Ex-NOR para diseñar un generador de paridad impar de 3 bits.
El circuito lógico de este generador se muestra en la figura siguiente, donde se aplican dos entradas a una puerta Ex-OR, esta salida Ex-OR y una tercera entrada se aplican a una puerta Ex-NOR. Se generan bits de paridad impares. También puede diseñar este circuito utilizando dos puertas Ex-OR y una puerta NOT.
comprobación de paridad
Un circuito lógico que busca errores que puedan ocurrir durante la transmisión. Este circuito puede ser un verificador de paridad par o un verificador de paridad impar, dependiendo del tipo de paridad generada en el transmisor. Cuando se utiliza este circuito como verificador de paridad par, el número de bits de entrada siempre debe ser un número par.
incluso comprobador de paridad
Considere que en el remitente se generan tres mensajes de entrada con bits de paridad pares. Estos 4 bits se aplican como entrada a un circuito verificador de paridad que verifica los datos en busca de posibles errores. Los datos se envían con paridad par, por lo que los 4 bits recibidos por el circuito deben contener un número par de unos.
Si se produce un error, el mensaje recibido consta de un número impar de unos. La salida del verificador de paridad se llama PEC (Verificación de errores de paridad).
La siguiente tabla muestra la tabla de verdad para el verificador de paridad par. PEC = 1 si ocurre un error, es decir, los 4 bits recibidos contienen un número impar de unos, y PEC = 0 si no ocurre ningún error, es decir, se envió un mensaje de 4 bits. Hay un número par de unos.
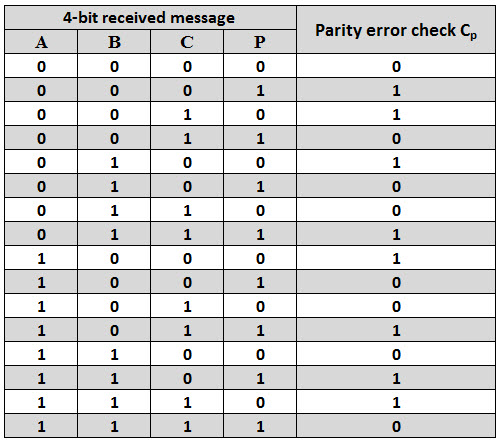
La tabla de verdad anterior se puede simplificar usando K-map como se muestra a continuación.
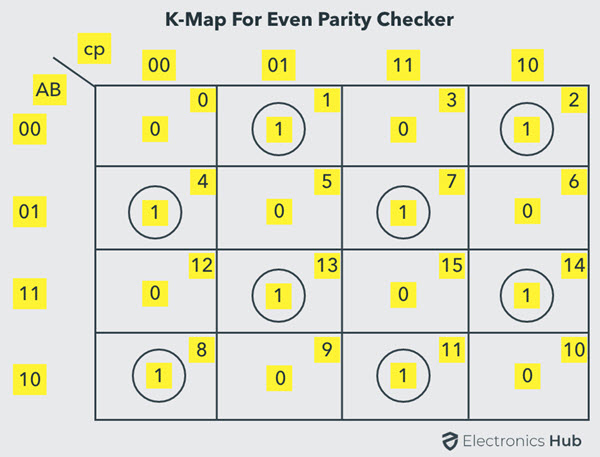
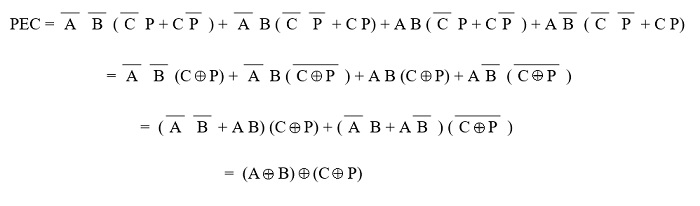
La fórmula lógica anterior para el verificador de paridad par se puede implementar utilizando tres puertas Ex-OR como se muestra en la figura. Si el mensaje recibido consta de 5 bits, se requiere otra puerta Ex-OR para verificar la paridad uniforme.
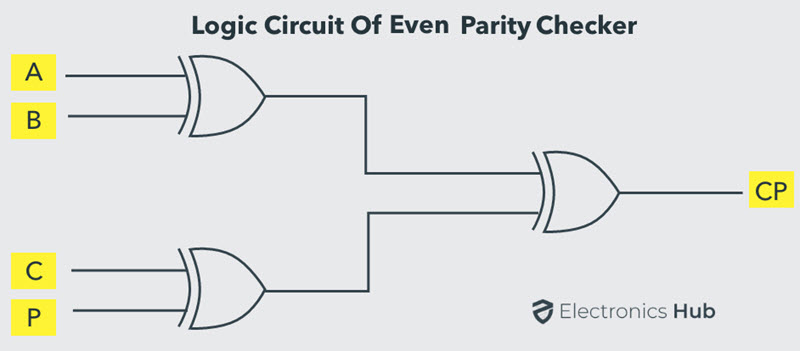
verificador de paridad impar
Supongamos que el remitente envía un mensaje de 3 bits y un bit de paridad impar. El circuito de verificación de paridad impar toma estos 4 bits y verifica si hay algún error en los datos.
Un número total impar de unos en los datos indica que no hay error, y un número total par de unos indica un error ya que los datos se envían con paridad impar al remitente.
La siguiente figura muestra la tabla de verdad para un generador de paridad impar. PEC = 1 si el mensaje de 4 bits recibido consta de un número par de unos (por lo que se produjo un error); PEC = 0 si el mensaje contiene un número impar de unos (es decir, el 1 es (significa no incluido) error) .
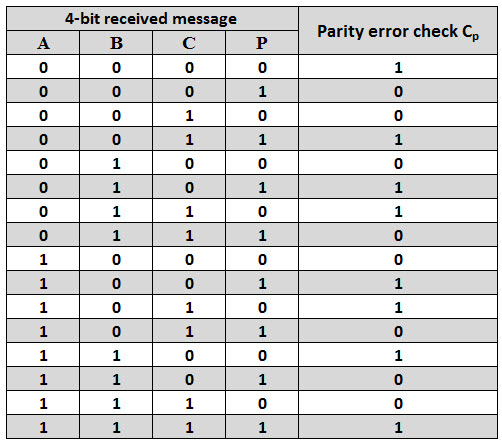
La expresión de PEC en la tabla de verdad anterior se puede simplificar mediante K-map como se muestra a continuación.
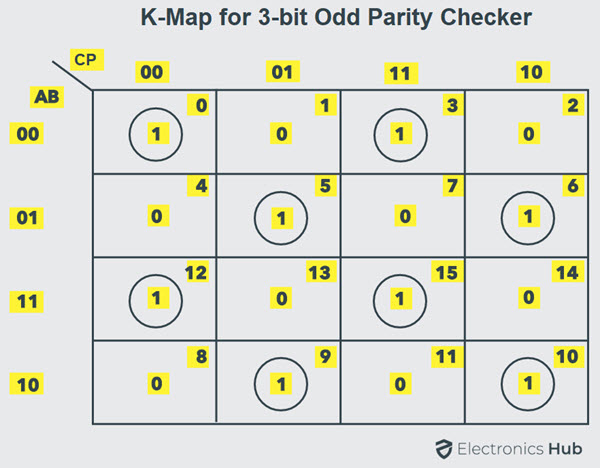
Simplificando, la expresión final de PEC se obtiene de la siguiente manera:
PEC = (A Ex-NOR B) Ex-NOR (C Ex-NOR P)
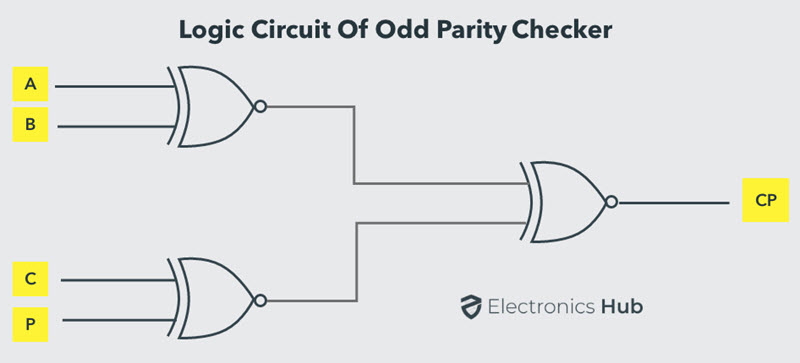
La fórmula del verificador de paridad impar se puede diseñar utilizando tres puertas Ex-NOR como se muestra a continuación.
Generador/comprobador de paridad IC
Hay diferentes tipos de circuitos integrados generadores/comprobadores de paridad disponibles en diferentes configuraciones de entrada, como 5 bits, 4 bits, 9 bits y 12 bits. Uno de los tipos de generadores/comprobadores de paridad más utilizados y estándar. El IC es 74180.
Este es un generador o verificador de paridad de 9 bits que se utiliza para detectar errores en sistemas de recuperación o transmisión de datos de alta velocidad. La siguiente figura muestra el diagrama de pines del 74180 IC.
Este IC se puede utilizar para generar códigos de paridad pares o impares de 9 bits o comprobar la paridad par o impar de códigos de 9 bits (8 bits de datos y 1 bit de paridad).
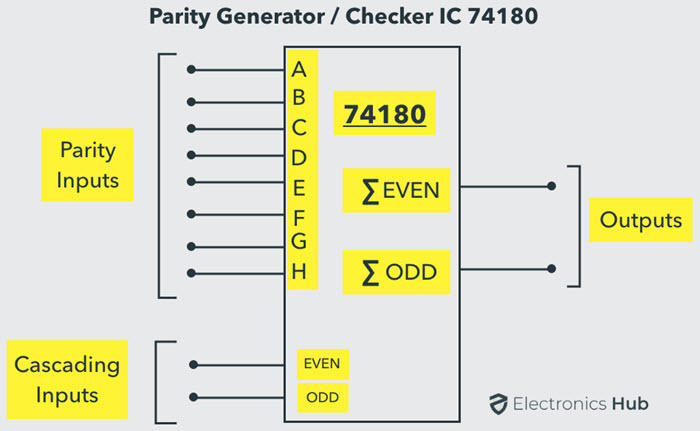
Este IC consta de ocho entradas de paridad A a H y dos entradas en cascada. Hay dos salidas: suma par y suma impar. Al implementar un circuito generador o verificador, los bits de paridad no utilizados deben conectarse al 0 lógico y las entradas en cascada deben ser iguales.
Si utiliza este IC como verificador de paridad par y se produce un error de paridad, la salida de ‘suma par’ bajará y la salida de ‘suma od’ subirá. Si este IC se utiliza como verificador de paridad impar, el número de bits de entrada debe ser impar, pero cuando ocurre un error, la salida “suma od” baja y la salida “suma par” sube.