El siguiente texto describe varios principios teóricos y matemáticos que funcionan detrás del procesamiento de geometría. También discutiremos cómo se aplican para diferentes propósitos al generar gráficos. A continuación, nos centraremos en las características destacadas del chip controlador de gráficos de alto rendimiento MB86296 de Fujitsu, centrándonos en la implementación del procesamiento geométrico. La parte final muestra cómo el rendimiento de MB86296 es mejor que el de sus predecesores debido a su motor de procesamiento de geometría mejorado.
Las operaciones de geometría, también llamadas transformaciones geométricas, consisten en operaciones matemáticas sobre coordenadas en gráficos 2D o 3D. Los ejemplos incluyen transformaciones de traslación, escala y rotación. Son esenciales para muchas aplicaciones gráficas y subrutinas. Por ejemplo, en una vista 3D de una ciudad, puede usar traducir para ubicar los símbolos de edificios y árboles, y rotarlos para orientarlos donde desee y escalarlos al tamaño correcto. Cada una de las tres transformaciones se puede utilizar en entornos 2D y 3D. Estas transformaciones consisten en cálculos matemáticos basados en coordenadas gráficas y, por lo tanto, son numéricamente intensivas y requieren una potencia de procesamiento considerable.
Fundamentos del procesamiento de geometría 2D/3D
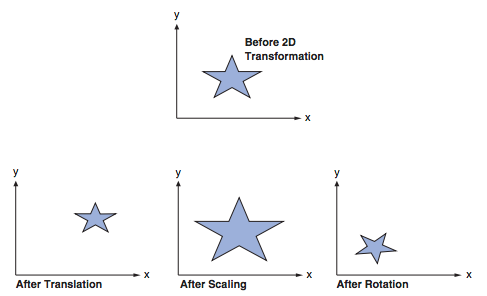
El siguiente diagrama destaca los conceptos básicos de las transformaciones 2D y 3D.
transformación 2D
Supongamos que tenemos un punto P(x, y) en un sistema de coordenadas 2D. Puede mover este punto a una nueva ubicación agregando una cantidad de traducción a los valores ‘x’ e ‘y’. Es decir, el punto se mueve al nuevo punto P(x’, y’) por _dx_ unidades a lo largo del eje x y _dy_ unidades a lo largo del eje y. podemos escribir:
[tex]xprime=x+d_{x},hspace{5mm}yprime=y+d_{y}[/tex]
Si definimos un vector columna
[tex]P=frac{x}{y},hspace {5mm}Pprime=frac{xprime}{yprime},hspace {5mm}T=frac{d_{x}}{d_{y}}[/tex]
Coordenadas homogéneas
A partir de estas fórmulas, está claro que la traducción se maneja de manera diferente a la rotación y el escalado. Necesito manejar las tres transformaciones de manera consistente para poder combinarlas en una sola expresión. Las coordenadas homogéneas resuelven este problema de manera muy efectiva. Para ello añadimos una tercera coordenada al punto. En lugar de estar representado por ‘x’ e ‘y’, cada punto ahora está representado por una W. Los dos conjuntos de coordenadas homogéneas son (2, 4, 6) y (2, 4, 6) y (4, 8, 12). Otra condición es que al menos una de las coordenadas homogéneas sea distinta de cero. Los puntos homogeneizados forman un plano definido por la fórmula W = 1 en el espacio (x, y, W).
Composición de transformaciones 2D
Considere una rotación de un objeto alrededor de un punto arbitrario P1. Ahora que sé cómo rotar un objeto alrededor de su origen, puedo resolver este problema dividiéndolo en las siguientes tareas:
- Traducir para que P1 sea el origen
- Girar
- Trasladar para que el origen vuelva a P1
Esto se muestra en la Figura 2.

conversión de ventana a viewport
Estas transformaciones se convierten de coordenadas mundiales a coordenadas de pantalla. Las coordenadas mundiales pueden ser una unidad de medida conveniente. Estos se utilizan para representar objetos en el mundo que está creando. La transformación entre dos coordenadas se puede realizar utilizando una matriz de transformación. Otra forma de lograr esto es especificar una región rectangular en coordenadas mundiales denominada ventana de coordenadas mundiales y una región rectangular correspondiente en coordenadas de pantalla denominada ventana gráfica a la que se asigna la ventana de coordenadas mundiales. Esta transformación se aplica a todas las primitivas de salida en coordenadas mundiales y se asigna a coordenadas de pantalla. Consulte la figura 3.