Tabla de contenido
Demostraciones, explicaciones, experimentos y ejemplos de soluciones de teoremas de compensación para el análisis de circuitos.
teorema de compensación
En la teoría de redes, es importante conocer y estudiar los efectos de los cambios de impedancia en una de las ramas. Afecta los voltajes y corrientes correspondientes en una red o circuito. Los teoremas de compensación proporcionan información sobre los cambios en la red.
El Teorema de Compensación se basa en el concepto básico de la Ley de Ohm. De acuerdo con la Ley de Ohm, cuando una corriente pasa a través de una resistencia, habrá una caída de tensión en la resistencia. Esta caída de tensión se opone a la tensión de alimentación.
Por lo tanto, conectamos una fuente de voltaje adicional con polaridad opuesta en comparación con el voltaje de suministro y la magnitud es igual a la caída de voltaje. El teorema de compensación se basa en este concepto.
El teorema de compensación es
“En toda red formada por impedancias lineales o bilaterales y fuentes independientes, para una rama con corriente I e impedancia Z creciente en ΔZ, los cambios de tensión y corriente en las demás ramas de la red se producen por una fuente de tensión opuesta de valor I∆ Z colocado en su rama después de reemplazar la fuente original con una impedancia interna.
Explicación del teorema de compensación
Para entender el teorema de compensación, considere el siguiente diagrama.
En esta figura, la fuente de voltaje V es una fuente de voltaje independiente con dos impedancias Z1 y Z2 Elementos lineales o de dos caras. Por lo tanto, podemos aplicar el teorema de compensación a esta red. La corriente a través del bucle es I.
Ahora suponga una impedancia Z.2 Aumentar en ΔZ. Este cambio hace que la corriente a través del bucle cambie a I’. El nuevo esquema se muestra a continuación.
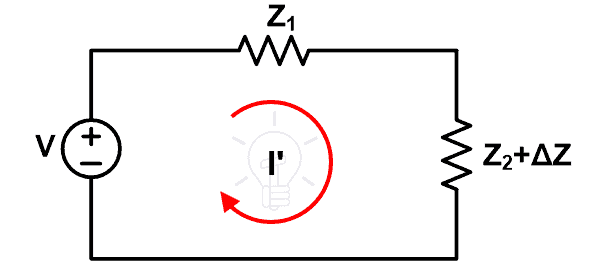
Debido al cambio de impedancia, el cambio de corriente viene dado por ΔI.
△I = I – I’
De acuerdo con el enunciado del teorema de compensación, podemos calcular directamente el cambio en la corriente ΔI. Para eso, tienes que cambiar el circuito.
La primera modificación es conectar una fuente de voltaje de valor I∆Z a la rama con impedancia variable. Y la polaridad de esta fuente de tensión es opuesta a la de la red. Fuente de voltaje V recién agregadaDecir ah conocida como la fuente de compensación.
ⅤDecir ah = I △z
El segundo cambio es que la fuente de voltaje anterior debe ser eliminada por la impedancia interna. Considerando una fuente de voltaje ideal en este estado, podemos eliminar esta fuente de voltaje cortocircuitando los terminales. Después de estos cambios, el resto del circuito se parece a la siguiente figura.
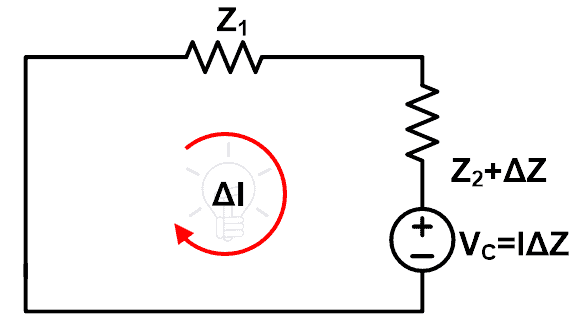
Resolviendo el circuito anterior, podemos encontrar fácilmente el cambio en la corriente después de que cambia la impedancia.
Prueba del teorema de compensación
Considere el circuito de la Figura 1. Calcule la corriente (I) a través del bucle.
Aplique KVL a la Figura-1.
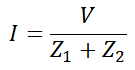
Aquí hemos asumido una impedancia Z.2 Varía con ΔZ. Y el circuito modificado se parece a la Figura-2. Necesitamos calcular la corriente (I’) a través del bucle en la Figura 2.
Aplique KVL a la Figura-2.
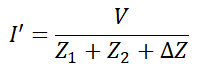
Debido al cambio de impedancia, el cambio en la corriente de bucle se expresa como ΔI. Además, ΔI es igual a la diferencia entre la antigua corriente I y la nueva corriente I’.
△I = I – I’
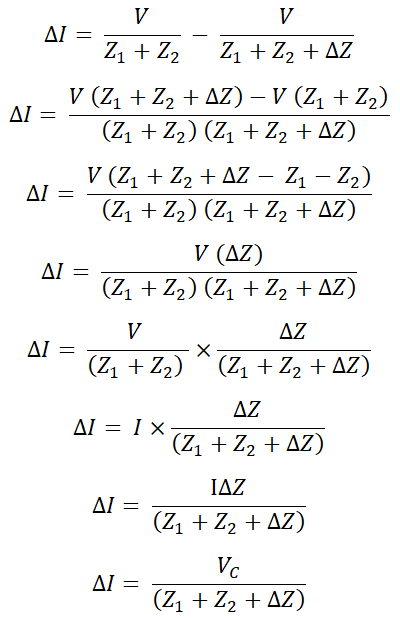
Ahora considere el siguiente diagrama.
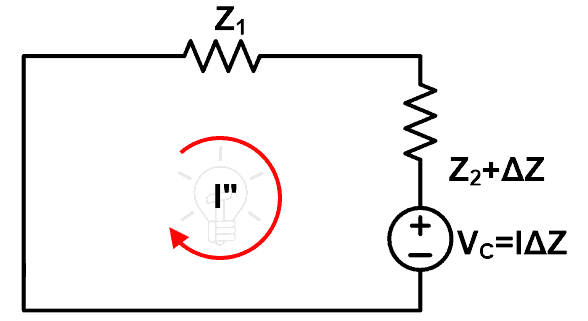
Esta figura representa el circuito después de implementar el teorema de compensación. Aquí, la fuente de voltaje original se elimina mediante un cortocircuito (suponiendo una fuente de voltaje ideal).
Podemos ver que la corriente pasa a través de este bucle. Luego compare esta corriente con la corriente calculada anteriormente.
Para calcular la corriente a través del bucle, aplique KVL a la figura anterior.
ⅤDecir ah = z1 I” +(z2 +Δz) I”
ⅤDecir ah = I” (z1 + z2 +Δz)
I” =VDecir ah / (z1 + z2 +Δz)
I” = ΔI
Por lo tanto, se demuestra que el cambio en la corriente (ΔI) después de la corrección es igual a la corriente calculada por el teorema de compensación.
También probamos el enunciado del teorema de compensación.
Experimento del teorema de compensación
objetivo: Demuestre el teorema de compensación y encuentre el cambio en la corriente.
Dispositivo: Voltímetro, amperímetro, resistencia, cable de conexión, protoboard,
diagrama de circuito:
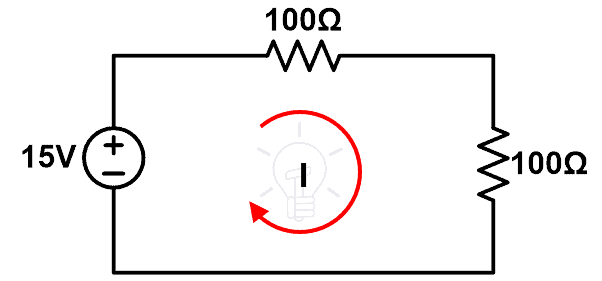
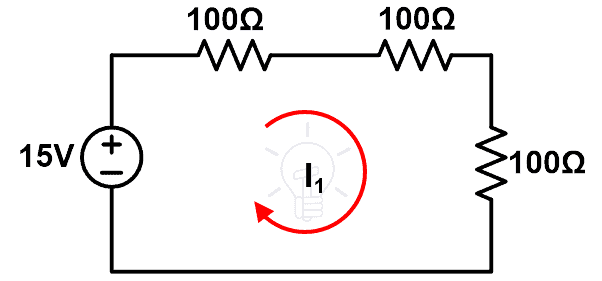
procedimiento:
Paso 1 Usando los cables de conexión en la placa de prueba, conecte los componentes como se muestra en la Figura 5.
Paso 2 Mida la corriente I.
Paso 3 Conecte los componentes como se muestra en la Figura 6. Aquí hemos conectado una resistencia adicional.
Paso 4 Mida la corriente I1.
Paso 5 Calcule el cambio en la corriente (ΔI) a partir de los valores de I e I1.
Paso 6 Conecte los componentes como se muestra en la Figura 7. Este circuito es un circuito de compensación.
Paso 7 Mida la corriente I.
Paso 8 Compare el cambio en la corriente (ΔI) con I”.
Tabla de experimentos:
resultado:
Comparando el valor de la corriente I” con ∆I, podemos probar el teorema de compensación.
Ejemplo del teorema de compensación
Ejemplo 1
- 1) Encuentre la corriente que fluye en la rama AB cuando la resistencia es de 3Ω.
- 2) Encuentre la corriente a través de la rama AB usando el teorema de compensación al cambiar una resistencia de 3Ω a 9Ω.
- 3) Demostrar el teorema de compensación.
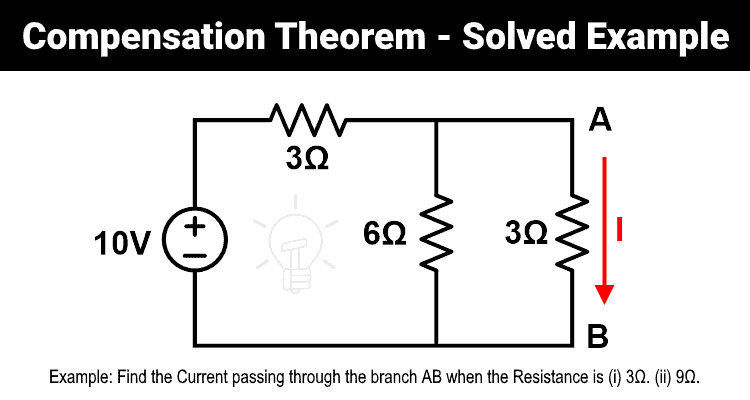
Respuesta 1
Las resistencias de 6 Ω y 3 Ω están conectadas en paralelo como se muestra. Y esta combinación en paralelo está conectada en serie con una resistencia de 3Ω.
rfórmula = 6 | | | 3+3
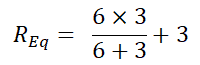
rfórmula = 2 + 3
rfórmula = 5Ω
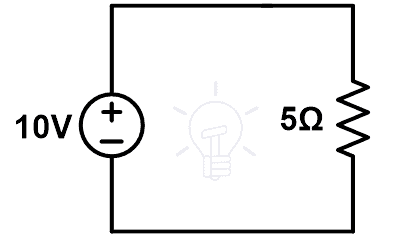
Según la ley de Ohm,
10 = I (Cinco)
I = 10 ÷ 5
I = 2A
Ahora necesitamos encontrar el camino actual a través de la rama AB. De acuerdo con las reglas de división actuales,
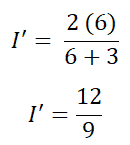
I’ = 1.333A (o 3/4A)
Respuesta-2
La resistencia de 3 Ω debe reemplazarse por una resistencia de 9 Ω. De acuerdo con el teorema de compensación, debemos agregar una nueva fuente de voltaje en serie con la resistencia de 9Ω. Y el valor de esta fuente de voltaje es:
ⅤDecir ah = I’ △z
dónde,
△z = 9 – 3 = 6 Ω y I’ = 4/3 A (o 1.333 A)
ⅤDecir ah = (4/3A) X 6Ω
ⅤDecir ah = 8V
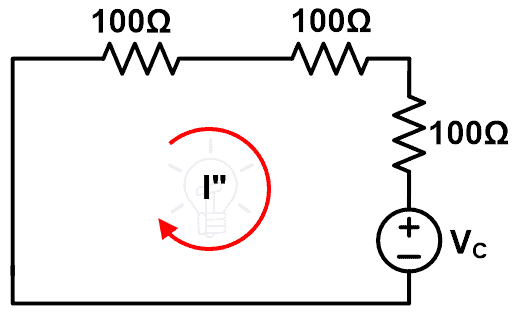
El esquema modificado o compensado se muestra en la siguiente figura.
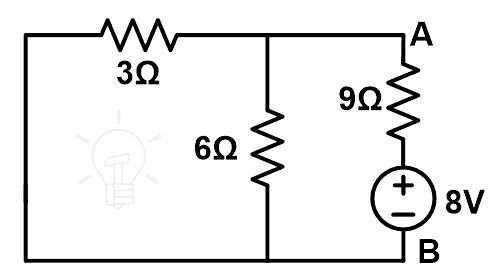
Luego encuentre la resistencia equivalente. Aquí, las resistencias de 3Ω y 6Ω están conectadas en paralelo. Esta combinación en paralelo se conecta luego en serie con una resistencia de 9 Ω.
rfórmula = 3 | | | 6 + 9
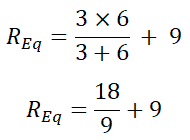
rfórmula = 2 + 9
rfórmula = 11Ω
Ahora, de acuerdo con la ley de Ohm,
Ⅴ = Δinfrarrojos
8 = ΔI (11Ω)
△I = 8 ÷ 11
△I = 0.7272A
Por lo tanto, de acuerdo con el teorema de compensación, el cambio de corriente es 0.7272A.
Respuesta-3
Quiero probar el teorema de compensación. Por lo tanto, usamos una resistencia de 9 Ω para calcular la corriente para el ejemplo dado.
El esquema modificado se muestra en la siguiente figura.
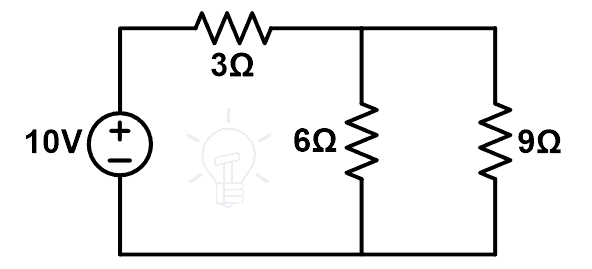
Aquí, las resistencias de 9 Ω y 6 Ω están conectadas en paralelo, y esta combinación en paralelo está conectada en serie con una resistencia de 3 Ω.
La resistencia equivalente será:
rfórmula = 9 | | | 6 + 3
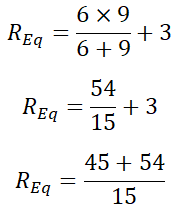
rfórmula = 99 ÷ 15
rfórmula = 6,66 Ω
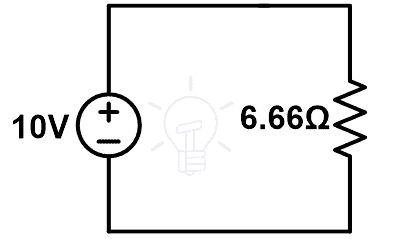
Del diagrama anterior;
10 = I (6.66)
I = 10 ÷ 6,66
I = 1.5151A
De acuerdo con las reglas de división actuales,
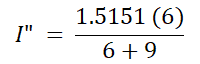
I” = 0.6060A
△I = I’ – I”
△I = (4/3A) – 0,6060
△I = 1.333A – 0.6060
△I = 0.7273A
Por lo tanto, se demuestra que el cambio de corriente calculado a partir del teorema de compensación es el mismo que el cambio de corriente calculado a partir del circuito original.
Ejemplo-2
En el siguiente circuito, use el teorema de compensación para encontrar el cambio en la corriente si reemplaza la resistencia de 3 Ω con una resistencia de 7 Ω. Y prueba el teorema de la compensación.
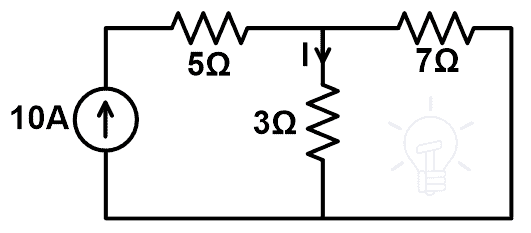
La red anterior consta solo de resistencias y fuentes de corriente independientes. Por lo tanto, podemos aplicar el teorema de compensación a esta red.
En esta figura la red es alimentada por una fuente de corriente. Ahora necesitamos encontrar la corriente a través de la rama de resistencia de 3Ω. Esta corriente se puede encontrar usando KCL o KVL. Pero aquí esta corriente se puede encontrar fácilmente por la regla de división actual.
Entonces, de acuerdo con las reglas de división actuales.
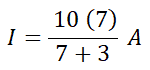
I = 70÷10A
I = 7A
En la red original con una resistencia de 3Ω, la corriente por esa rama es de 3A. Ahora necesitamos cambiar esta resistencia de 3Ω a 7Ω. Este cambio modifica la corriente que pasa por esa rama. Y encontramos este cambio en la corriente por el teorema de compensación.
Para eso, necesitamos crear una red de compensación. Para crear una red de compensación, necesitamos acortar las fuentes de voltaje y abrir las fuentes de corriente para eliminar todas las fuentes independientes disponibles en la red.
Solo una fuente actual está disponible en esta red. Suponga que la fuente de corriente es una fuente de corriente ideal. Por lo tanto, no se requiere resistencia interna adicional.
El segundo cambio que debemos hacer en el compensador es agregar una fuente de voltaje adicional. Y el valor de este voltaje es:
ⅤDecir ah = I △z
ⅤDecir ah = 7 × (7 – 3)
ⅤDecir ah = 7 × 4
ⅤDecir ah = 28V
La red de compensación se muestra a continuación.
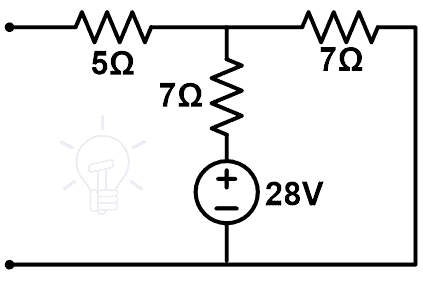
Solo hay un bucle en este diagrama. Y la corriente que pasa por la rama de 7Ω da el cambio de corriente (ΔI).
△I = ⅤDecir ah ÷ (7+7)
△I = 28 ÷ 14
△I = 2A
Para probar el teorema de compensación, encuentre la corriente en el circuito con la resistencia de 7Ω. El esquema modificado se muestra en la siguiente figura.
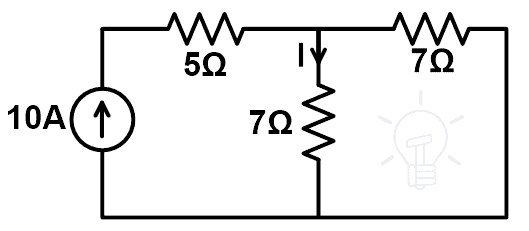
I” = (10 (7)) ÷ (7 + 7)
I” = 70 ÷ 14
I” = 5A
Aplicar las reglas de división actuales.
Para encontrar el cambio en la corriente, debemos restar esta corriente de la corriente que pasa por la red original.
△I = I – I”
△I = 7 – 5
△I = 2A
Esto prueba el teorema de la compensación.
Tutoriales de análisis de circuitos eléctricos relacionados:
