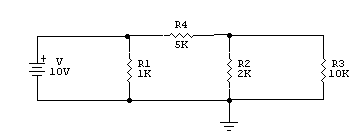
En tutoriales anteriores, explicamos que las resistencias se pueden conectar en circuitos en serie o en paralelo y usar la ley de Ohm para obtener la corriente y el voltaje. Para crear circuitos más complejos usando combinaciones de resistencias, se pueden usar combinaciones tanto en serie como en paralelo en el mismo circuito. Este tipo de circuito utiliza conexiones tanto en serie como en paralelo en lo que se denomina un circuito compuesto o combinacional, como se muestra en la Figura 1. y voltaje
Análisis de circuitos combinacionales
Una estrategia básica para analizar circuitos combinacionales implica transformar el circuito combinacional en un circuito en serie utilizando la semántica de resistencia equivalente de ramas paralelas. Una vez convertido a un circuito en serie, el análisis se puede realizar de la forma habitual. Al igual que en el tutorial anterior, el método para determinar la resistencia equivalente en paralelo es el mismo. La resistencia total o equivalente de estas ramas es igual a la resistencia de una rama dividida por el número de ramas. Para las resistencias acopladas, el método de cálculo de la resistencia equivalente es el mismo que para los circuitos individuales en serie o en paralelo. Esto se debe a que las resistencias en serie transportan exactamente la misma corriente y las resistencias en paralelo ven exactamente el mismo voltaje.
Procedimiento de cálculo serie-paralelo
La resistencia total del circuito combinado se obtiene reduciendo las diversas combinaciones en serie y en paralelo a una sola resistencia equivalente del circuito cuya corriente se puede determinar fácilmente. Al deshacer el proceso de reducción, se puede obtener la corriente que fluye a través de cada resistencia. Para llevar a cabo el proceso de reducción se deben considerar los siguientes puntos:
1. Dos o más resistencias con sus cabezas conectadas directamente y sus colas directamente en paralelo. Se puede reducir a una sola resistencia utilizando la ecuación de resistencia equivalente para resistencias en paralelo.
2. Dos resistencias conectadas de manera que una cola se conecta a la siguiente cabeza están en serie sin otro camino para que la corriente fluya a lo largo de la línea que las conecta, y una resistencia equivalente se puede reducir a
ejemplo
Calcule la corriente total (I) extraída del suministro de 12V.

Esto puede parecer una tarea difícil al principio, pero si miras de cerca verás que hay dos resistencias, R2 y R3, ambas conectadas en serie. Para esta combinación, la resistencia resultante es

Por lo tanto, ambas resistencias, R2 y R3, se pueden reemplazar con un solo valor de resistencia (12 ohmios).

Aquí se crea una sola resistencia RA en paralelo con la resistencia R4. Esto se puede reducir a un solo valor de resistencia, R(com), usando la fórmula para dos resistencias conectadas en paralelo:

El nuevo circuito simplificado se ve así:

Las dos resistencias restantes R1 y R(com) están conectadas en serie y se pueden sumar para obtener la resistencia total del circuito entre los puntos A y B.


El circuito de combinación original de cuatro resistencias anterior ahora se puede reemplazar con una sola resistencia de solo 12 ohmios. El valor de la corriente del circuito (I) se puede calcular como:

Referencias
http://www.electronics-tutorials.ws/resistor/res_5.html
http://www.physicsclassroom.com/class/circuits/u9l4e.cfm