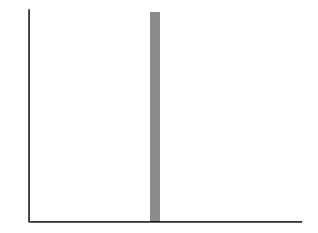Muchos ADC se utilizan para medir el nivel o la magnitud de las señales estáticas. Las aplicaciones incluyen mediciones de peso, presión y temperatura. Estas aplicaciones involucran señales de bajo nivel que requieren alta resolución y precisión. Un ejemplo es una báscula que puede manejar cargas de hasta 5 kg y puede resolver mediciones de hasta 10 miligramos.
Cuando se utilizan ADC de alta resolución, es necesario comprender los errores y el ruido asociados con el proceso de conversión. El propósito de esta nota de aplicación es mostrar cómo cuantificar el rendimiento estático mediante el análisis de histogramas. Se recopila un conjunto de datos de muestra y se utiliza para medir el ruido y la compensación. Se utilizan métodos estadísticos para determinar la “bondad” y los intervalos de confianza asociados con las estimaciones. El promedio se trata como un medio para reducir la incertidumbre y mejorar la resolución.
Explicación del histograma de ruido
Por lo general, no hay un PDF que describa el ruido del ADC. Este PDF se puede deducir mediante pruebas estáticas. Esta PDF estimada es en realidad un gráfico de histograma de ocurrencias de variables aleatorias y variaciones individuales. Para los ADC, la variable aleatoria es el código digital resultante, por lo que la frecuencia a la que se produce cada código se representa frente a cada código discreto.
Un ADC silencioso siempre tendrá el mismo código de salida para un voltaje de entrada dado. En la Figura 1 se muestra un gráfico de histograma del convertidor sin ruido. Un gráfico de histograma del código de salida contendrá múltiples valores si hay una fuente de ruido en el ADC. La figura 2 es un histograma que muestra que la salida de una entrada puede ser uno de 11 códigos posibles.

El ruido eléctrico debido a efectos aleatorios forma una distribución gaussiana o normal. Esta es una curva en forma de campana llamada curva normal. La PDF gaussiana es continua y está completamente determinada especificando la media (µ) y la varianza (σ2). El PDS gaussiano está definido por

norte=1 para archivos PDF reales.
Otros valores norte Escale el PDF para que se ajuste al conjunto de muestra. Utilizando los datos que se muestran en la Figura 3, podemos estimar la PDF. La Figura 3 traza el histograma ADC ruidoso y la PDF estimada. Las medias y las varianzas se estimaron a partir de un conjunto de datos de muestra. Estos parámetros de PDF nos permiten cuantificar el rendimiento del ADC. La media es el valor medio o esperado. Se utiliza para medir el error de compensación. La varianza describe la variabilidad de una distribución con respecto a su media. Se utiliza como medida de incertidumbre o ruido. La raíz cuadrada de la varianza se denomina desviación estándar (σ) y es una medida del ruido efectivo o rms. El ruido de pico a pico se puede determinar a partir del valor de ruido RMS.

No todos los tipos de ruido se pueden medir con la PDF gaussiana. Al estimar la PDF utilizando una distribución normal o gaussiana, el ruido debe ser aleatorio. La figura 4 muestra el histograma del ruido no aleatorio. Tenga en cuenta que la distribución del histograma no tiene la forma familiar de campana. Los histogramas pueden ser el resultado de una interferencia de línea de 60 Hz u otros tipos de ruido sinusoidal. El PDF se parece al de una sinusoide con una distribución “puntiaguda”.

La figura 5 es otro ejemplo de un PDF sin forma gaussiana. La razón aquí es la baja no linealidad diferencial (DNL) del ADC. Un DNL bajo da como resultado anchos de código desiguales y distribuciones sesgadas. Los ADC Delta-sigma y de autocalibración tienen buenas especificaciones DNL. Un buen DNL es muy importante para las aplicaciones que utilizan promedios para mejorar la resolución.

El histograma debe tener una distribución en forma de campana. De lo contrario, la PDF gaussiana estimada no se correlacionará o la PDF gaussiana estimada no se correlacionará con el sistema real. Es una buena idea ver la distribución del ruido para asegurarse de que se esté analizando el ruido aleatorio. Si el ruido no es aleatorio, el histograma no se puede modelar utilizando la ecuación PDF de Gauss.