🕑 Tiempo de lectura: 1 minuto
Puede analizar barras de refuerzo con diferentes secciones transversales, propiedades del material y dimensiones bajo carga axial para determinar los valores de tensión y deformación correspondientes.
El análisis se basa en las ecuaciones básicas de la ley de Hooke relacionadas con las tensiones (F) y tensión (e)
pedo = mi.MI ———-Fórmula 1
donde “E” es el módulo elástico. Aquí hay una breve descripción del análisis de tensión o deformación de barras de refuerzo con diferentes secciones transversales.
Lea también: Diferentes constantes elásticas y sus relaciones
Tabla de contenido
Análisis de barras en diferentes tramos
Suponga una carga axial de ‘P’ en barras de diferentes longitudes, áreas transversales y diámetros, como se muestra en la Figura 1.
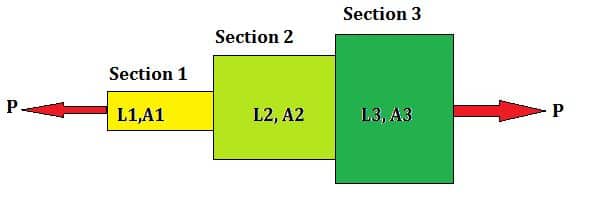
Incluso si la carga axial que actúa sobre la barra es la misma, los esfuerzos y las deformaciones longitudinales experimentadas por cada sección de la barra son diferentes. La derivación se sigue de los siguientes principios:
Cambio total de longitud, dL = suma de los cambios de longitud de la sección 1, la sección 2 y la sección 3.
dL = dL1 +dL2 +dL3 ———-Fórmula 2
1. ANÁLISIS DE LA SECCIÓN 1
tensiones en la sección 1,
pedo1 = carga/área de la sección 1 = P/A1
Cepa de la Sección 1,
mi1 = cambio de longitud / longitud original = dL1/L1 = pedo1/E = P/(A1MI) [From Eq.1]
Por lo tanto, el cambio en la longitud dL1=PL1/(A1E) ———-Ec.3
2. ANÁLISIS DE LA SECCIÓN 2
tensiones en la sección 2,
pedo2 = carga/área de la sección 2 = P/A2
mi2 = cambio de longitud / longitud original = dL2/L2 = pedo2/E = P/(A2MI) [From Eq.1]
Por lo tanto, el cambio en la longitud dL2=PL2/(A2E)———-Ec.4
2. ANÁLISIS DE LA SECCIÓN 2
Sección 3 estrés
pedo3 = carga/área de la sección 3 = P/A3
mi3 = cambio de longitud / longitud original = dL3/L3 = pedo3/E=P/(A3MI) [From Eq.1]
Por lo tanto, el cambio en la longitud dL3=PL3/(A3E)———-Ec.5
De la ecuación 2,
dL = dL1 +dL2 +dL3
Por lo tanto, Eq.3 + Eq.4 + Eq.5,
dL = DL1 +dL2 +dL3 =PL1/(A1E) +PL2/(A2E) + PL3/(A3MI)
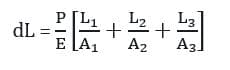
La fórmula anterior se utiliza cuando las secciones de la barra tienen el mismo módulo de elasticidad. Para diferentes valores de ‘E’, obtenemos la siguiente relación:
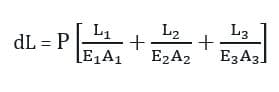
Lea también: Relaciones tensión-deformación en el hormigón
Lea también: Relación esfuerzo-deformación del refuerzo
