frecuencia armónica

introducción

El término “armónico” se refiere a la frecuencia fundamental de una forma de onda. Antes de aprender sobre los armónicos, es necesario comprender algunos conceptos de formas de onda. Analicemos el tema de las frecuencias naturales y forzadas.

[adsense1]

frecuencia natural

La vibración cuando un objeto vibra libremente sin estar sometido a una fuerza externa se llama “vibración natural”. La frecuencia a la que se produce la vibración natural se llama “frecuencia natural”.

frecuencia forzada

Cuando un objeto vibra aplicando una fuerza periódica desde el exterior, esa vibración se denomina “vibración forzada”. La frecuencia de vibración forzada se llama “frecuencia forzada”.

onda viajera

Cuando una onda se mueve continuamente a través de un medio sin reflejarse en ningún punto de su trayectoria, se llama onda viajera.

onda estacionaria

Cuando dos ondas viajeras de la misma frecuencia y amplitud viajan en direcciones opuestas a través de un medio, se superponen. Esta onda superpuesta se llama “onda estacionaria”. Una onda estacionaria tiene nodos y antinodos.

Volver a la cima

frecuencia fundamental

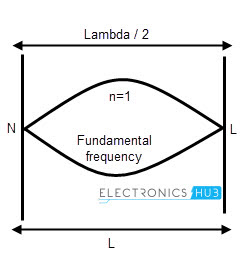
Definida como la frecuencia más baja de una forma de onda periódica. Generalmente se escribe como “f”. En otras palabras, la frecuencia de resonancia más baja de un cuerpo en vibración se llama “frecuencia fundamental”.

Volver a la cima

¿Qué es armónico?

Los armónicos son frecuencias que son múltiplos enteros de la frecuencia fundamental. Las vibraciones resonantes forzadas de un objeto generan ondas estacionarias. La frecuencia natural forma un patrón de onda estacionaria. Estos patrones se crean en frecuencias específicas y se denominan “frecuencias armónicas” o “armónicos”.

El sonido de las frecuencias armónicas producidas por la forma de onda es muy claro, pero otras frecuencias producen ruido que impide escuchar el sonido claro de las ondas.

[adsense2]

Los armónicos ocurren en todas las formas de onda, pero con mayor frecuencia solo en ondas sinusoidales. Las ondas no sinusoidales, como las ondas triangulares y en dientes de sierra, se construyen agregando frecuencias armónicas. La palabra “armónicos” se usa comúnmente para describir la distorsión causada por varias frecuencias no deseadas llamadas “ruido” en una onda sinusoidal.

Cada armónico encuentra dos posiciones: un nodo y un antinodo.

nodo

Un nodo es un punto a lo largo del medio que parece estar estacionario. No hay desplazamiento. Por eso, también se les llama puntos y también nodos.

estómago

Hay una partícula que sufre un desplazamiento máximo entre dos puntos. Los dos puntos son nodos. Aquí, un nodo es positivo y el otro es negativo. Los ganglios y el vientre se muestran en la imagen de abajo.

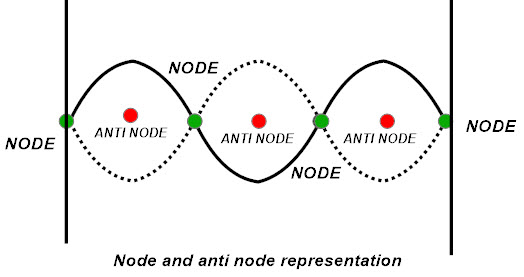
Los nodos y antinodos se presentan en forma de ondas. Por tanto, las ondas contienen frecuencias armónicas. La frecuencia fundamental es la frecuencia más baja de los armónicos. Por tanto, entre ellos sólo hay un vientre. Este vientre está a medio camino entre los dos nodos. De esto podemos decir que la cuerda de la guitarra produce la longitud de onda más larga y la frecuencia más baja.

La frecuencia más baja producida por cualquier instrumento musical se llama frecuencia fundamental. Esto también se conoce como el “primer armónico” de la onda. En términos de frecuencia fundamental, podemos decir que los armónicos son múltiplos enteros de la frecuencia fundamental.

Por ejemplo: f, 2f, 3f, 4f, etc… son armónicos.

Como la frecuencia fundamental es un número entero, hay n armónicos: 1.º armónico, 2.º armónico, 3.º armónico, etc.

primer armónico

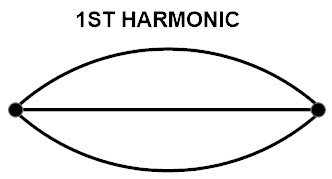
Como se explicó anteriormente, la frecuencia fundamental también se llama primer armónico. El primer armónico tiene dos nodos y un antinodo.

segundo armónico

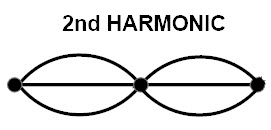
El segundo armónico consta de tres nodos y dos antinodos. Puedes obtener el segundo armónico estableciendo un nodo entre los dos nodos del primer armónico. Para el primer armónico, el segundo nodo está entre el primero y el último nodo.

tercer armónico

Para el tercer armónico, si los nodos están en cualquiera de los extremos de la púa, el patrón de forma de onda resultante constará de cuatro nodos y tres antinodos. Esto significa que la forma de onda del tercer armónico tiene un ciclo sinusoidal completo y medio ciclo. Si lo dibujas como un diagrama, se verá como el siguiente.

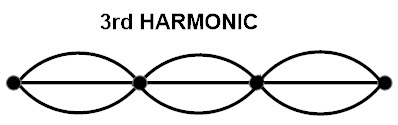
Observando la discusión anterior, podemos decir que el número de antinodos es igual a un múltiplo entero de un armónico particular. Es decir, para el primer armónico hay un antinodo y para el segundo armónico hay dos antinodos.
La frecuencia armónica se puede calcular mediante la siguiente fórmula:

Velocidad = Frecuencia x Longitud de onda

V = nx λ

norte^th Armónicos = nx frecuencia fundamental

Si conocemos la velocidad y la longitud de onda de la forma de onda, podemos calcular las frecuencias armónicas. Hay dos tipos de armónicos en las ondas: armónicos pares y armónicos impares. Por ejemplo, un cilindro que está abierto por ambos lados vibrará con armónicos pares e impares, pero un cilindro que está cerrado por un lado vibrará solo con armónicos impares.

Volver a la cima

Características armónicas

La mayoría de las vibraciones que escuchamos son causadas por armónicos. Por ejemplo, la música puede sonar como una guitarra, un violín o incluso una voz humana. Los armónicos también se denominan parciales armónicos. Las características de los armónicos varían según la vibración y la forma de onda del instrumento.

Por tanto, las vibraciones son generalmente las responsables de generar armónicos. Un oscilador no es más que un instrumento que se mueve o vibra. Los armónicos parciales producen frecuencias diferentes a las de los armónicos totales. Sin embargo, las frecuencias armónicas precisas se producen mediante instrumentos con cables largos y delgados.

Sólo produce exactamente un armónico. Las frecuencias que ocurren en múltiplos enteros de la frecuencia fundamental se denominan frecuencias armónicas.

El oído humano no puede oír claramente todos los armónicos. Las frecuencias distintas de las armónicas se denominan frecuencias no armónicas. Se combinan muchos armónicos para formar un sonido. Los sonidos discordantes son audibles para el oído humano.

Original: La primera es ver la campana de nuestra escuela y de la iglesia con regularidad. En segundo lugar, los cuencos cantores antiguos son otro ejemplo de vibración sólo en frecuencias armónicas. Otra propiedad importante de los armónicos es que todos los armónicos son periódicos en la frecuencia fundamental y la suma de los armónicos también es periódica en la frecuencia fundamental.

Volver a la cima

matices y matices

Las frecuencias superiores a la frecuencia fundamental se denominan “armónicos”. Los instrumentos musicales generalmente tienen matices. Los armónicos varían según el tono del instrumento. Así como diferentes instrumentos tienen diferentes timbres, también los tienen los armónicos. Al mezclar/combinar armónicos, puedes obtener el tono fundamental del instrumento.

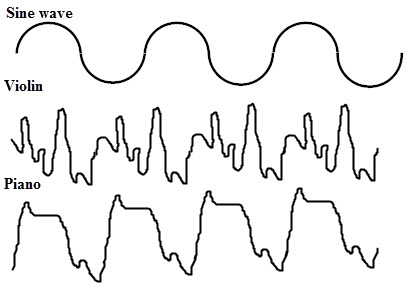
Observe la salida de sonido anterior producida por diferentes instrumentos como el violín y el piano. Tienen la misma frecuencia, por lo que tienen el mismo sonido, diferentes armónicos y, en última instancia, diferentes sonidos. Esto significa que los armónicos del instrumento pueden afectar la salida del sonido. La forma de onda irregular de un violín representa un sonido agudo, mientras que un piano produce un sonido puro similar a una onda sinusoidal.

Volver a la cima

Relación entre longitud y longitud de onda.

Verifique todos los armónicos nuevamente para obtener la relación entre longitud y longitud de onda. Es decir, el primer, segundo y tercer armónico. Todos sabemos que la longitud de onda de una onda sinusoidal es “lambda”. Los armónicos también se representan como ondas sinusoidales.hagamos los cálculos

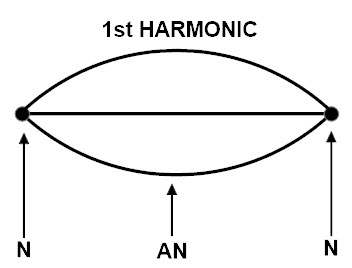
desde el primer armónico

Por tanto, en el primer armónico, ambos extremos de la cuerda quedan fijos y se denominan nodos. Y cuando hay vibración, el cable se mueve hacia arriba y hacia abajo, formando un antinodo. Entonces este diagrama parece una media onda sinusoidal.Esa es la mitad de la longitud de onda.

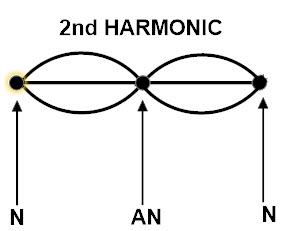
desde el segundo armónico

El segundo armónico tiene dos antinodos, por lo que hay dos bucles. A partir del primer armónico ya hemos calculado que un bucle es igual a 1/2 longitud de onda. Entonces aquí tenemos dos bucles, que suman una longitud de onda.

Del 3er armónico

En el movimiento del tercer armónico hay tres bucles, cada uno de los cuales consta de 1/2 longitud de onda. Entonces la suma de los tres bucles es 3/2 de lambda.

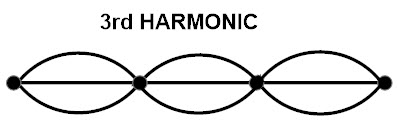
De todos estos armónicos, podemos decir que para el primer armónico hay un antinodo, para el segundo armónico hay dos antinodos y para el tercer armónico hay tres antinodos. Por tanto, el enésimo armónico tiene n antinodos.

Por lo tanto, si derivamos la expresión de la relación entre longitud y longitud de onda, obtenemos:

L=n/2 de longitud de onda

Estas expresiones también se pueden escribir como:

Para 1er armónico: L=1/2-lambda

Para el segundo armónico: 2L=2/2-lambda

Para tercer armónico: 3L=3/2-lambda

Para el enésimo armónico tenemos: nL=n/2-lambda donde ‘n’ es un número entero.

La relación entre la longitud armónica y la longitud de onda y la relación matemática también se muestran a continuación en forma de tabla.

L=n/2 (lambda)

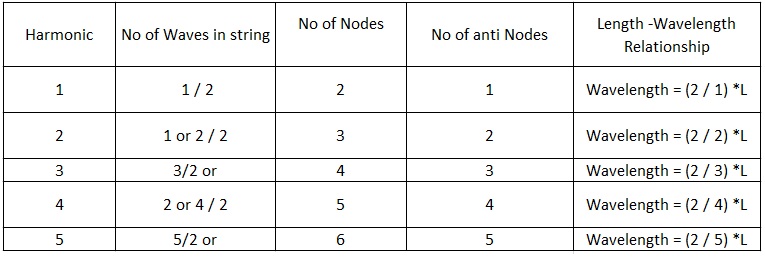
Volver a la cima

Desventajas de los armónicos

• Los armónicos afectan el rendimiento de los sistemas de energía. Las desventajas de los armónicos se enumeran a continuación.
• Los armónicos degradan la calidad del suministro de energía en la red eléctrica. Puede causar algunos efectos negativos.
• Los armónicos pueden aumentar la corriente RMS efectiva, provocando pérdidas de energía en el sistema de distribución.
• El aumento acumulativo del tercer armónico provoca una sobrecarga en el conductor neutro.
• Los armónicos aumentan el nivel de ruido de las señales eléctricas.
• Los armónicos pueden alterar la tensión de alimentación y provocar un mal funcionamiento de las cargas sensibles.
• Las armónicas causan problemas con las comunicaciones y las líneas telefónicas.
• Estos afectan la resonancia entre la inductancia de la fuente y el nivel de capacitancia del capacitor de factor de potencia.

En pocas palabras, los armónicos causan los siguientes errores en los sistemas de energía y comunicación:

• equipo de calefacción
• Falla en el equipo
• Mal funcionamiento del equipo
• interferencia de comunicación
• Mal funcionamiento de fusibles y disyuntores
• problemas de proceso
• Calentamiento de conductores.

Volver a la cima

Ejemplo armónico

Ya sabemos que encontramos muchas frecuencias armónicas en nuestra vida diaria. A continuación se muestran algunos ejemplos de armónicos.

Example

Muchos osciladores, como cuando tocas la cuerda de una guitarra, oscilan en diferentes frecuencias, pero no son armónicos, sino que generalmente se les llama subarmónicos. Por lo tanto, si utiliza un oscilador largo y delgado, se generarán frecuencias en el rango armónico. Para saber exactamente dónde ocurren los armónicos, primero debemos calcular la frecuencia fundamental de la forma de onda.

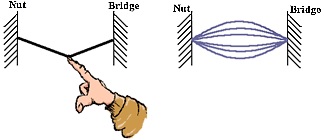
Considere una cuerda de guitarra que produce frecuencias de armónicos. Luego deja el extremo de la cuerda sujeto y asegúralo a la estructura de tu guitarra. Por tanto, los extremos no se pueden mover. Por tanto, ya sabemos que los armónicos se generan por ondas estacionarias. Para ellos hay nudos y barrigas.

Aquí ambos extremos son nudos, por lo que hay nudos y también una barriga. Por tanto, tiene sus propias frecuencias armónicas. Por lo tanto, dado que la frecuencia fundamental es la frecuencia más pequeña, hay un antinodo entre ellas. Este vientre está a medio camino entre los dos nodos. De esto podemos decir que la cuerda de la guitarra produce la longitud de onda más larga y la frecuencia más baja.

La frecuencia más baja producida por cualquier instrumento musical se llama frecuencia fundamental. A esto también se le llama primer armónico.

Volver a la cima