Un oscilador de cristal es un circuito oscilante que utiliza un cristal como resonador para estabilizar o controlar la frecuencia. A menudo se utilizan para generar relojes para circuitos analógicos y sistemas digitales.
[adsense1]
Se utilizan en aplicaciones como relojes, transmisores de comunicaciones y receptores que requieren una mayor estabilidad, es decir, mantener con precisión una frecuencia de oscilación precisa. En un oscilador LC, la frecuencia está determinada por los valores de inductancia y capacitancia.
Sin embargo, dichas variables pueden cambiar debido a las fluctuaciones del clima, el tiempo y la temperatura. Por lo tanto, los osciladores LC no son adecuados para aplicaciones de estabilidad de frecuencia. Sin embargo, en el caso de un oscilador de cristal, el cristal es el elemento determinante de la frecuencia que proporciona estabilidad de alta frecuencia.
Tabla de contenido
¿Qué es un cristal?
Los cristales son elementos producidos sintéticamente o de origen natural que exhiben efectos piezoeléctricos. El efecto piezoeléctrico es un fenómeno electromecánico en el que cada vez que se aplica presión mecánica a un conjunto de caras de un cristal, se crea una diferencia de potencial en la cara opuesta del cristal. Por lo tanto, cada vez que una fuerza hace que el cristal vibre, se genera un voltaje alterno a través del cristal.
Por el contrario, cuando se aplica un voltaje alterno a un cristal, se producen vibraciones mecánicas que provocan distorsiones mecánicas en la forma del cristal. Estas vibraciones u oscilaciones oscilan a una frecuencia de resonancia determinada por el corte y el tamaño físico del cristal.
[adsense2]
Esto se debe a que cada cristal tiene su propia frecuencia de resonancia dependiendo de su corte. Por tanto, genera una señal de frecuencia constante bajo la influencia de vibraciones mecánicas.
La imagen de arriba muestra simbólicamente una fina rodaja de cuarzo en un recinto sellado. Básicamente, tiene forma hexagonal con una pirámide al final. Sin embargo, en la práctica corta en rodajas de losa rectangulares.
Los procesos de corte incluyen corte X, corte Y, corte AT, etc. Luego, esta losa se instala entre dos placas metálicas. Estas placas de metal se denominan placas de retención porque sujetan las losas de cristal entre ellas.
Los cristales están disponibles desde unos pocos KHz hasta unos pocos MHz, con factores de calidad de miles a cientos de miles. Estos valores de factor de alta calidad hacen que los cristales sean muy estables con respecto a la temperatura y el tiempo.
Circuito equivalente de cristal.
Cuando el cristal está estable, es decir, no vibra, equivale a una capacitancia debido a su unión mecánica. Esta capacitancia se llama capacitancia de montaje CM y existe entre dos placas metálicas separadas por un dieléctrico como una losa de cristal. Este CM es la capacidad de derivación.
Cuando el cristal comienza a vibrar, experimenta pérdidas por fricción interna, representadas por la resistencia R. Por otro lado, como el cristal tiene cierta masa, su inercia está representada por la inductancia L. Durante condiciones de vibración, el cristal exhibe cierto grado de rigidez, denotado por. condensador C
Por tanto, los tres elementos R, L y C son las propiedades del cristal natural y CM es la capacitancia de los electrodos que sostienen el cristal. Todos estos valores están determinados por el corte, el tamaño y la naturaleza vibratoria del cristal. El circuito equivalente de todo el cristal se muestra a continuación.
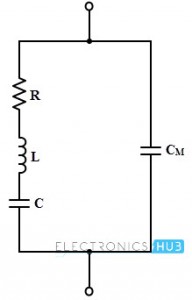
Estos parámetros RLC forman un circuito resonante y la frecuencia resonante se expresa como:
fr = (1/ (2π √ (LC))) √ (Q2 / (1 + Q2))
donde Q es el factor de calidad y su valor es igual a 2 π f L/R. El valor Q de los cristales es muy alto, normalmente 20.000. Por tanto, el factor √ (Q2/(1 + Q2) es 1. En este caso, la frecuencia de resonancia es:
fr = (1/ (2π √ (LC))
De hecho, la frecuencia del cristal es inversamente proporcional al espesor. Por tanto, para conseguir frecuencias muy altas, el espesor debe ser muy fino. Sin embargo, las vibraciones pueden dañar el cristal. Por lo tanto, los osciladores de cristal se utilizan en el rango de frecuencia de aproximadamente 200 o 300 KHz.
Resonancia en serie y resonancia en paralelo.
Del circuito equivalente de un oscilador de cristal, podemos ver que el circuito tiene dos frecuencias resonantes: una frecuencia resonante en serie y una frecuencia resonante en paralelo. La resonancia en serie ocurre cuando las reactancias de los tramos RLC en serie son iguales, es decir, XC = XL.
En la frecuencia resonante en serie, la reactancia del brazo LC en serie es cero, y la única impedancia proporcionada por esta rama en resonancia en serie es R. Esta frecuencia de resonancia en serie se expresa como:
fs = (1/ (2π √ (LC))
Una condición resonante en paralelo ocurre cuando la reactancia del tramo resonante en serie es igual a la reactancia del capacitor montado. La reactancia del brazo en serie se vuelve inductiva a frecuencias superiores a fs. En esta condición resonante, la impedancia que presenta el cristal al circuito externo es muy alta.
La capacitancia equivalente durante la resonancia en paralelo es la siguiente.
Ceq = CMETRO C/CMETRO+C
La frecuencia de resonancia paralela viene dada por:
fp = (1/ (2π √ (LCeq))
La siguiente figura muestra la relación entre la impedancia del cristal y la frecuencia cuando el valor de capacitancia del tramo de la serie es mucho menor que CM.
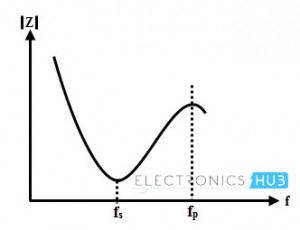
En general, fp y fs están tan cerca que se dice que en realidad sólo hay una frecuencia de resonancia en un cristal.
oscilador de cristal de colpitts
Los osciladores de cristal de Colpitts se utilizan principalmente en altas frecuencias de radio como osciladores estables que utilizan un cristal para controlar la frecuencia del oscilador.
La retroalimentación generalmente se proporciona a través de una configuración de divisor de voltaje capacitivo externo, pero también se puede proporcionar a través de un elemento capacitor. La siguiente figura muestra un circuito Colpitts de emisor común que utiliza un esquema de retroalimentación capacitiva externa.
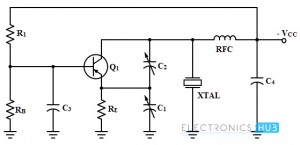
En el circuito anterior, las resistencias R1 y RB proporcionan la polarización del divisor de voltaje para facilitar el arranque, y C3 es un capacitor de derivación que aísla efectivamente la base de las fluctuaciones de RF. Los condensadores C1 y 2 están conectados entre el colector y el emisor para fines de retroalimentación.
Estos dos condensadores variables proporcionan regulación y control de retroalimentación. El cristal está conectado entre el colector y tierra y funciona como un circuito resonante paralelo.
El colector se alimenta a través de RFC junto con C4, que actúa como circuito de aislamiento de energía. La salida se puede tomar capacitivamente en el terminal del colector.
cirugía
El funcionamiento de este oscilador de cristal está determinado por el funcionamiento del circuito divisor de voltaje que consta de los condensadores C1 y C2. Cuando se enciende el circuito, una pequeña corriente de polarización fluye a través de RB. Luego fluye una corriente de colector, creando un voltaje a través del divisor del capacitor.
- Supongamos que la corriente del colector aumenta debido a un pulso de ruido generado dentro del transistor. Esto reduce el voltaje del colector y el capacitor C2 acopla este cambio de voltaje al emisor.
- Una señal negativa decreciente (dirección positiva) aplicada al emisor es regenerativa. Esto aumenta aún más la corriente del colector.
- El voltaje del colector continúa disminuyendo (el voltaje negativo se vuelve positivo) y el capacitor C2 continúa acoplando este voltaje de carga al emisor.
- Al mismo tiempo, aparece un cambio en el voltaje del colector a través del cristal. Por lo tanto, el cristal se distorsiona ligeramente mecánicamente por la acción piezoeléctrica.
- Una vez que la corriente del colector alcanza el nivel de saturación, no se producen más cambios y se detiene la operación regenerativa.
- En este punto, la tensión electrostática a través del cristal comienza a disminuir, el capacitor C1 comienza a descargarse ligeramente a través de RE y finalmente la corriente del colector comienza a disminuir. Esta operación también es regenerativa y el transistor pasa inmediatamente al modo de corte.
- A medida que la corriente del colector disminuye, el voltaje del colector aumenta (se vuelve más negativo) y el cristal se esfuerza en la dirección opuesta.
- Por lo tanto, a medida que continúa cada ciclo de esta operación, el cristal oscila a su frecuencia de resonancia paralela. La oscilación del cristal genera un voltaje a través del cristal, por lo que una vez que comienza la oscilación, el cristal continúa oscilando.
- Dado que el cristal se desvía del colector a tierra, actúa efectivamente como un circuito resonante paralelo, suavizando el pulso oscilante en una forma de onda aproximadamente sinusoidal.
Los osciladores de cristal también se pueden diseñar con una variedad de configuraciones de circuitos. Otros tipos más comunes de configuraciones de circuitos incluyen los osciladores de cristal Miller y los osciladores de cristal Pierce.
reloj de cristal con microprocesador
Hemos comentado que los osciladores de cristal se utilizan para generar oscilaciones con mayor estabilidad de frecuencia. Ésta es la razón por la que los osciladores de cristal se utilizan para generar señales de reloj en sistemas digitales. Esto se debe a que los microprocesadores y controladores ejecutan instrucciones en sincronización con las señales del reloj.
Ciertos tipos de controladores tienen circuitos osciladores incorporados y solo requieren un cristal para generar la señal de reloj requerida. Es posible que ciertos dispositivos digitales no tengan una unidad osciladora incorporada, por lo que se requiere un circuito oscilador externo para generar los pulsos de reloj.
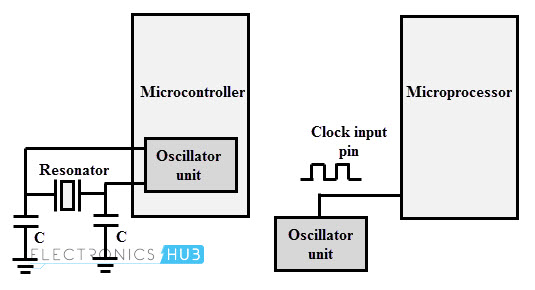
La figura anterior muestra un ejemplo del uso de un oscilador de cristal para generar la frecuencia de reloj de un microprocesador. Para los microcontroladores, un oscilador de cristal es suficiente. El valor del circuito oscilador y del cristal se determina en función del valor de la frecuencia máxima de reloj a la que puede funcionar el sistema.
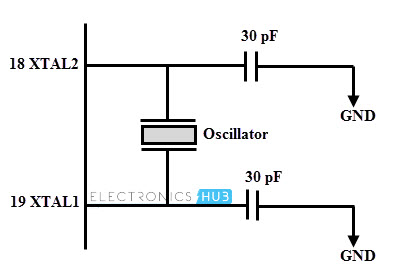
La siguiente figura muestra un microcontrolador 8051 que funciona según un oscilador de cristal externo. A menudo se conecta un oscilador de cristal entre los pines de entrada XTAL1 y XTAL2.
XTAL1 es la entrada al amplificador del oscilador inversor y la entrada al circuito de generación de reloj interno, y XTAL2 es la salida del amplificador del oscilador inversor. Para los microcontroladores 8052, las frecuencias de cristal más utilizadas son 12 MHz y 11,059 MHz, aunque 11,059 es mucho más común.
Problema de ejemplo
El cristal tiene los siguientes parámetros: CMETRO = 1 pF, R = 5 K ohmios, L = 0,4 H, C = 0,085 pF. A continuación, encuentre la frecuencia de resonancia en serie, la frecuencia de resonancia en paralelo y el factor de calidad del cristal.
A partir de los conceptos de resonancia en paralelo y en serie explicados anteriormente, la frecuencia de resonancia en serie se puede expresar como:
fs = (1/ (2π √ (LC))
= (1/ (2π √ (0,4 × 0,085 × 10-12))
= 0,856MHz
La frecuencia de resonancia paralela viene dada por:
fp = (1/ (2π √ (LCeq))
La capacitancia equivalente durante la resonancia en paralelo es la siguiente.
Ceq = CMETRO C/CMETRO +C
= (0,085 × 1) / (0,085 + 1)
= 0,078 pF
fp = (1/ (2π √ (LC))
= (1/ (2π √ (0,4 × 0,078 × 10-12))
= 0,899MHz
Factor de calidad Q = ws L / R
= 2π fs L/R
= (2π × 0,856 × 106 × 0,4) / 5 × 103
= 430.272