Los mapas de Carnot o mapas K fueron introducidos en 1953 por el ingeniero de telecomunicaciones de Bell Laboratories, Maurice Carnot, como un refinamiento de los “diagramas de Veitch de Edward Veitch”, un método para simplificar o reducir la complejidad de las expresiones booleanas.
El método de Karnaugh o K-map es una representación gráfica de ecuaciones booleanas que utiliza operaciones booleanas para reducir la complejidad de resolverlas. Se pueden considerar versiones especiales o ampliadas de “tablas de verdad”.
Un diagrama de Karnaugh puede describirse como “una matriz que contiene 2k celdas en un formato similar a una cuadrícula, donde k es el número de variables en la expresión booleana que se reducirán u optimizarán”. Dado que se evalúa a partir del método de la tabla de verdad, cada celda del mapa K representa una sola fila de la tabla de verdad y las celdas están representadas por cuadrados.
Las celdas en el k-map están dispuestas de manera que se asignan diferentes conjunciones de una sola variable a filas adyacentes. El método K-map apoya la eliminación de posibles condiciones de carrera y permite una identificación rápida.
La técnica del mapa de Karnaugh se puede utilizar para reducir expresiones booleanas que contienen cualquier número de variables, como expresiones booleanas de 2 variables, expresiones booleanas de 3 variables, expresiones booleanas de 4 variables e incluso expresiones booleanas de 7 variables, que son complejas de resolver. . Utilice los teoremas y leyes booleanos habituales.
descripción general
Tabla de contenido
Minimización con mapas de Karnaugh y ventajas de K-maps
- Los mapas K se utilizan para convertir tablas de verdad de ecuaciones booleanas en forma SOP minimizada.
- Reglas básicas fáciles y sencillas para la simplicidad.
- El método K-map es más rápido y eficiente que otras técnicas de simplificación del álgebra booleana.
- Todas las filas del mapa K se representan mediante celdas cuadradas, donde cada cuadrado representa un minitérmino.
- Es fácil convertir tablas de verdad en k-maps y convertir k-maps en ecuaciones en forma de suma de productos.
Hay dos formas de convertir una ecuación booleana en un mapa K.
- forma no optimizada
- forma optimizada
- Forma no optimizada: implica convertir el número de unos en la ecuación SOP a un número igual de términos producto (términos mínimos).
- Forma optimizada: implica reducir el número de minitérminos en la ecuación SOP.
Agrupación de variables del mapa K
- Hay algunas reglas a seguir al agrupar variables en un K-map.ellos son
- Un cuadrado que contenga “1” debe tomarse al menos una vez en la simplificación.
- Un cuadrado que contiene un “1” se puede considerar tantas veces como se pueda agrupar.
- Los grupos no deben contener ceros (0).
- Los grupos deben ser lo más grandes posible.
- Los grupos pueden ser horizontales o verticales. Las variables no se pueden agrupar en diagonal.
- Si no hay posibilidad de que el cuadrado que contiene “1” se coloque en un grupo, se debe agregar a la fórmula final.
- Los grupos pueden superponerse.
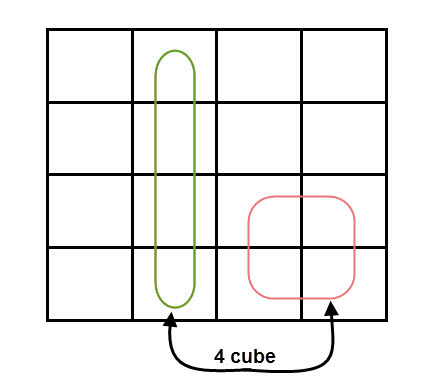
- El número de cuadrados en un grupo debe ser igual a una potencia de 2, como 1, 2, 4, 8, etc.
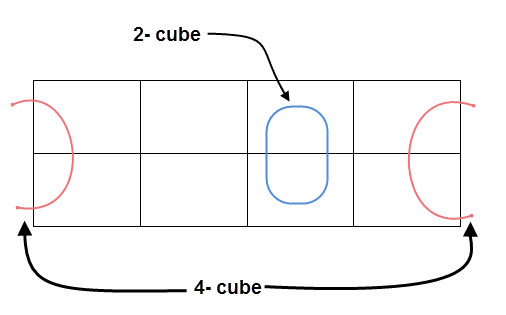
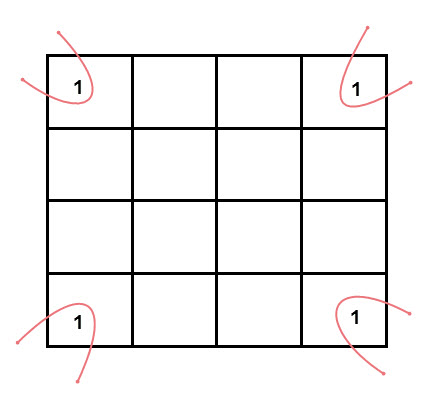
- Los grupos pueden moverse. Los K-maps se consideran esféricos o plegados, por lo que los cuadrados de las esquinas (al final de las columnas o filas) deben considerarse cuadrados adyacentes.
- La agrupación de variables de K-map se puede realizar de varias maneras, por lo que las ecuaciones simplificadas resultantes no siempre tienen que ser únicas.
- Para dibujar un K-map, las ecuaciones booleanas deben estar en forma normal.

Mapa K de 2 variables
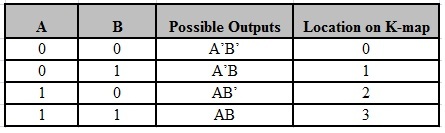
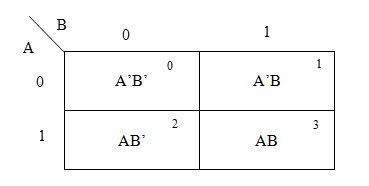
El mapa k de dos variables tiene cuatro celdas (22). Se verá así (ver imagen a continuación)

Los términos mínimos posibles de dos variables (A y B) son AB, A.B’, A’.B y A’.B’. La conjunción de las variables (A, B) y (A’, B) está representada en las celdas de la fila superior, y (A, B’) y (A’, B’) están representadas en las celdas de la fila inferior. . . La siguiente tabla muestra las ubicaciones de todas las salidas posibles de una función booleana de dos variables en el K-map.
A continuación se muestra una representación general de un gráfico K-map de dos variables.
Cuando utilice mapas de Karnot para simplificar ecuaciones booleanas, represente cada celda del mapa K que contenga un término conectado con un 1. Luego agrupe las celdas adyacentes en tamaños posibles de 2 o 4. Para k-maps más grandes, puede agrupar variables por tamaños más grandes, como 8 o 16.
Los grupos de variables deben ser rectangulares. Es decir, los grupos deben formarse uniendo células adyacentes vertical u horizontalmente. No se permiten grupos diagonales o en forma de L. El siguiente ejemplo muestra la simplificación de K-map de una ecuación booleana de dos variables.
ejemplo
Simplifique la ecuación booleana de dos variables dada utilizando un mapa K.
F = XY’ + X’ Y + X’Y’
Primero, creemos una tabla de verdad para la ecuación dada.
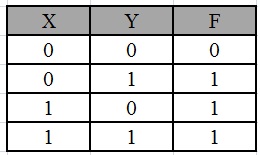
Coloca 1 en el término de salida dado por la ecuación.
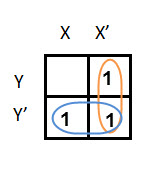
Este K-map le permite crear dos grupos de acuerdo con las reglas de agrupación. Uno es combinar los términos (X’, Y) y (X’, Y’), y el otro es combinar (X, Y’) y (X’, Y’). (X’, Y’) término. Aquí ambos grupos utilizan la celda inferior derecha.
Después de agrupar las variables, el siguiente paso es determinar la expresión minimizada.
Al reducir cada grupo, obtenemos la intersección de las expresiones minimizadas, por ejemplo quitando el término común de los dos grupos, X’ e Y’. Por tanto, la ecuación reducida queda como X’ +Y’.
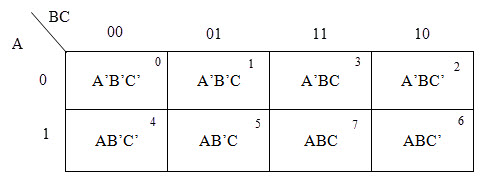
Mapa K de tres variables
Para una función booleana de tres variables, puede haber ocho términos mínimos de salida. A continuación se muestra una representación general de todos los minitérminos con tres variables.
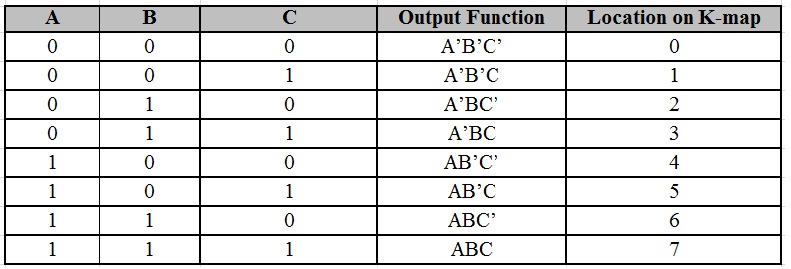
A continuación se muestra un gráfico típico de un mapa K de tres variables. Debido a que las columnas 10 y 11 han intercambiado posiciones, puede ver que solo una variable cambia entre celdas adyacentes. Este cambio le permite minimizar la lógica.
Para K-maps de 3 variables, puede agrupar hasta 8 celdas. Otras posibilidades son 1, 2 y 4.
ejemplo
Simplifique la ecuación booleana dada en tres variables usando k-map.
F = X’ YZ + X’ Y’ Z + XY Z’ + X’ Y’ Z’ + XYZ + XY’ Z’
Primero, creemos una tabla de verdad para la ecuación dada.
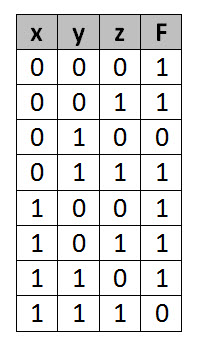
Coloca 1 en el término de salida dado por la ecuación.
El mapa k de tres variables tiene ocho celdas (23). Se verá así (ver imagen a continuación).
El tamaño máximo del grupo es de 8 personas, pero dependiendo de la situación es posible formar grupos de 4, 2, etc. Un mapa de Karnot de tres variables considera que la columna más a la izquierda del mapa k es una columna adyacente de la columna más a la derecha. Por tanto, un grupo de tamaño 4 se forma de la siguiente manera:
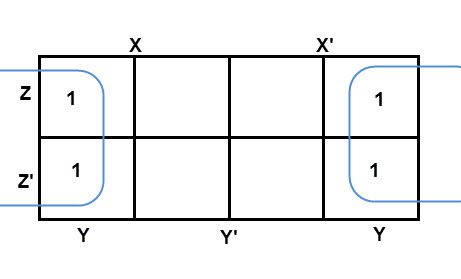
Y lo que ambos términos tienen en común es “Y”. Por tanto, un grupo de tamaño 4 se reduce como unión Y. Para consumir todas las celdas que contienen 1, agrupe las celdas restantes para formar un grupo de tamaño 2, como se muestra a continuación.
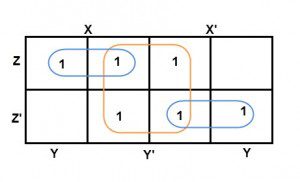
Los grupos de tamaño 2 no tienen variables comunes, por lo que se describen mediante esas variables y sus conjugados. Por lo tanto, la ecuación reducida queda como XZ’ + Y’ + X’ Z. No es posible realizar más minimizaciones con esta ecuación.
4 mapas K variables
Para una función booleana de cuatro variables, existen 16 términos mínimos posibles. A continuación se muestra una representación general de minitérminos que utiliza cuatro variables:
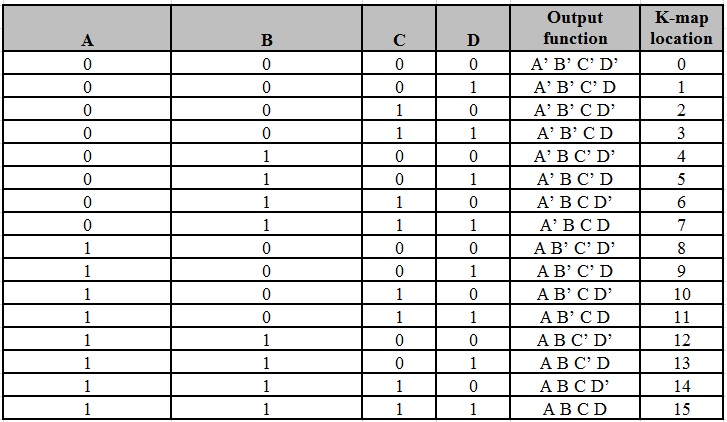
A continuación se muestra un gráfico típico de K-map de 4 variables. Puede ver que se han intercambiado tanto las columnas como las filas de 10 y 11.
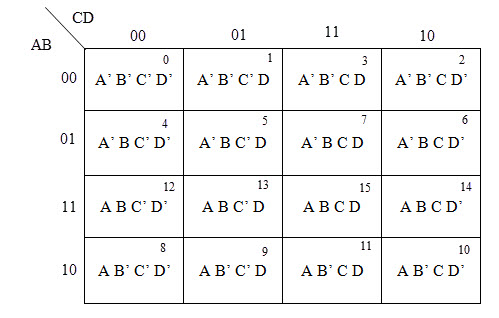
El número de celdas que se pueden agrupar es 1, 2, 4, 8 o 16.
ejemplo
Simplifique la ecuación booleana de cuatro variables dada usando k-map. F (W, X, Y, Z) = (1, 5, 12, 13)
Sol: F (W, X, Y, Z) = (1, 5, 12, 13)

Al preparar un k-map, podemos minimizar la ecuación booleana dada de la siguiente manera.
F = WY’Z + W’Y’Z
5 mapas K variables
Una función booleana de 5 variables puede contener hasta 32 mintérminos. Todos los términos mínimos posibles se enumeran a continuación.
| a | B | C | D | mi | función de salida | Ubicación del mapa K |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | A B C D E’ | 0 |
| 0 | 0 | 0 | 0 | 1 | A B C D E | 1 |
| 0 | 0 | 0 | 1 | 0 | A be ka de | 2 |
| 0 | 0 | 0 | 1 | 1 | Abekadé | 3 |
| 0 | 0 | 1 | 0 | 0 | A B C D E’ | cuatro |
| 0 | 0 | 1 | 0 | 1 | A B C D E | Cinco |
| 0 | 0 | 1 | 1 | 0 | A B C D E’ | 6 |
| 0 | 0 | 1 | 1 | 1 | A B C D E | 7 |
| 0 | 1 | 0 | 0 | 0 | A B C D E’ | 8 |
| 0 | 1 | 0 | 0 | 1 | A B C D E | 9 |
| 0 | 1 | 0 | 1 | 0 | A B C D E’ | Diez |
| 0 | 1 | 0 | 1 | 1 | A B C D E | 11 |
| 0 | 1 | 1 | 0 | 0 | A B C D E’ | 12 |
| 0 | 1 | 1 | 0 | 1 | A B C D E | 13 |
| 0 | 1 | 1 | 1 | 0 | A B C D E’ | 14 |
| 0 | 1 | 1 | 1 | 1 | A B C D E | 15 |
| 1 | 0 | 0 | 0 | 0 | A B C D E’ | dieciséis |
| 1 | 0 | 0 | 0 | 1 | A B C D E | 17 |
| 1 | 0 | 0 | 1 | 0 | A B C D E’ | 18 |
| 1 | 0 | 0 | 1 | 1 | abstenerse | 19 |
| 1 | 0 | 1 | 0 | 0 | A B C D E’ | 20 |
| 1 | 0 | 1 | 0 | 1 | A B C D E | veintiuno |
| 1 | 0 | 1 | 1 | 0 | A B C D E’ | Veintidós |
| 1 | 0 | 1 | 1 | 1 | A B C D E | veintitrés |
| 1 | 1 | 0 | 0 | 0 | A B C D E’ | veinticuatro |
| 1 | 1 | 0 | 0 | 1 | A B C D E | Veinticinco |
| 1 | 1 | 0 | 1 | 0 | A B C D e” | 26 |
| 1 | 1 | 0 | 1 | 1 | A B C D E | 27 |
| 1 | 1 | 1 | 0 | 0 | A B C D E’ | 28 |
| 1 | 1 | 1 | 0 | 1 | A B C D E | 29 |
| 1 | 1 | 1 | 1 | 0 | A B C D E’ | 30 |
| 1 | 1 | 1 | 1 | 1 | A B C D E | 31 |
El mapa K de 5 variables tiene 32 celdas como se muestra a continuación. Representado por F(A, B, C, D, E). Está dividido en dos cuadrículas de 16 celdas y una variable (A) es 0 en una cuadrícula y 1 en la otra.
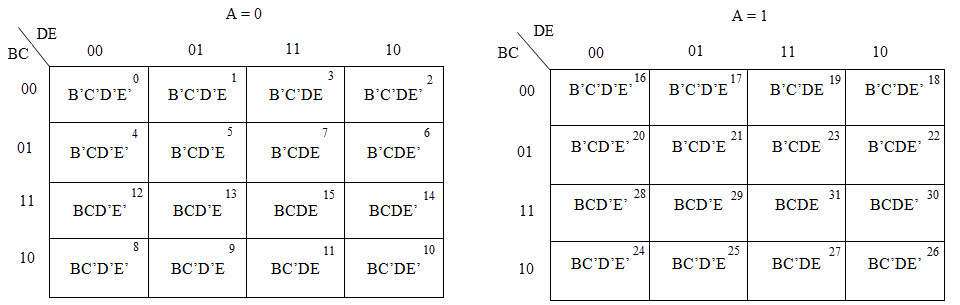
ejemplo
Simplifique la ecuación booleana de 5 variables dada usando k-map.
f (A, B, C, D, E) = ∑ metro (0, 5, 6, 8, 9, 10, 11, 16, 20, 42, 25, 26, 27)
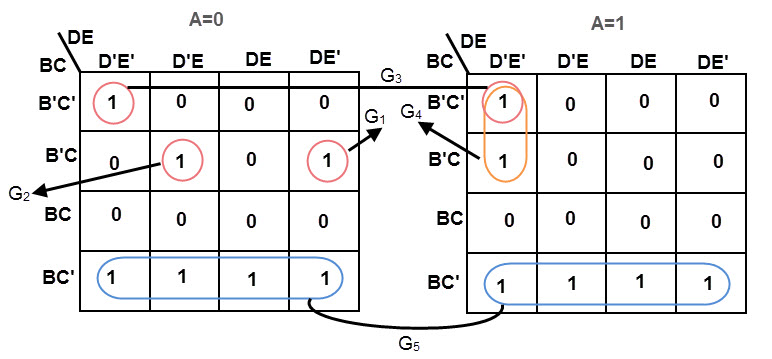
K-map para condiciones “no importa”
Las condiciones “No me importa” se utilizan para reemplazar celdas vacías y formar posibles grupos de variables. Estos se pueden utilizar como 0 o 1 según las variables vecinas del grupo. Las celdas que contienen condiciones “no importa” están representadas por un asterisco.
Un símbolo entre el 0 y el 1 normal.
También puede ignorar “no me importa” al agrupar variables. Las condiciones de “no importa” son muy útiles para agrupar variables grandes.
Minimizar expresiones usando Don’t CaresPuede minimizar una expresión booleana buscando una función relativa para la condición “no importa” y asignándole 0 o 1. Si n es el número de no importa en la expresión booleana, entonces el número de funciones obtenidas es: 2norte
.
Implementación de un conversor de código BCD a Gray usando K-map
Un código Gray es una secuencia de números en la que dos números consecutivos difieren en un bit. Este código recibió su nombre del científico “Frank Gray”. Poseía una patente en 1953 para el uso de cordón gris en registros de eje.
Puede utilizar la simplificación de k-map para convertir códigos decimales codificados en binario (BCD) en códigos Gray.
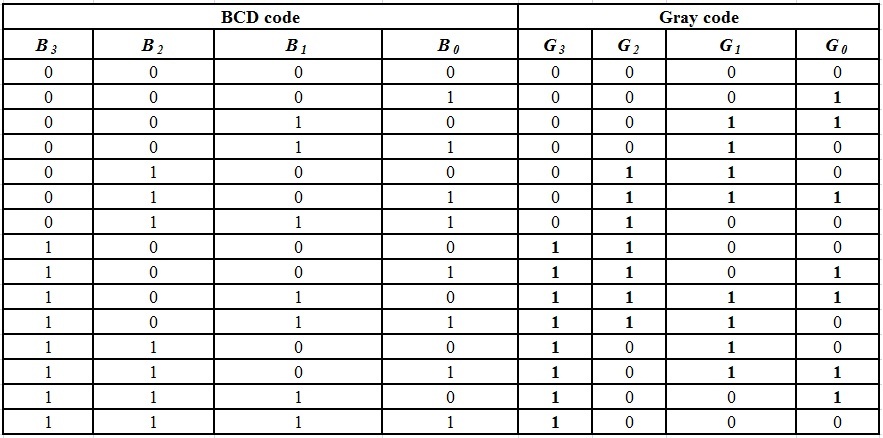
Código BDC y código Gray
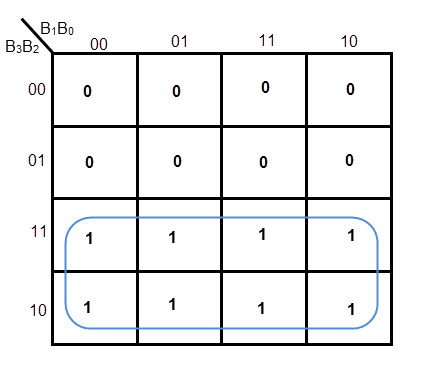
K-MAP para G3
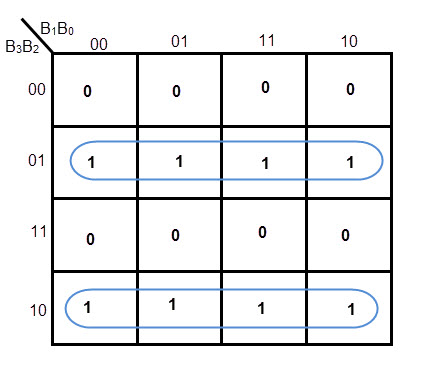
K-MAP para G2
Fórmula de cálculo G2 = B3′ B2 + B3 B2’= B3 XOR B2
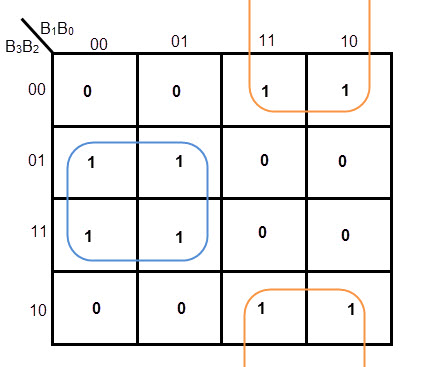
K-MAP PARA G1
Fórmula de cálculo para G1 = B1′ B2 + B1 B2’= B1 XOR B2
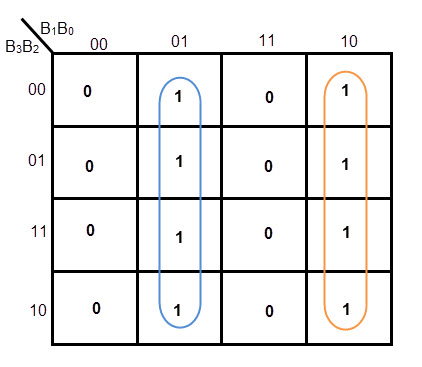
mapa G0K
Fórmula de cálculo para G0 = B1′ B0 + B1 B0’= B1 XOR B0
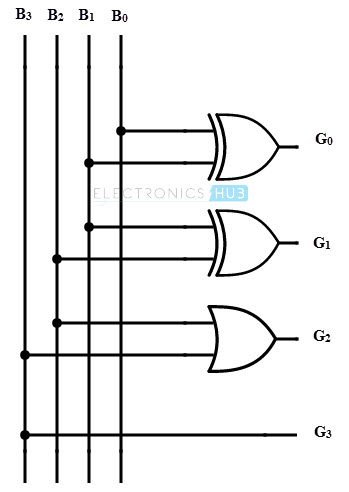
BCD a gris
- Artículo relacionado:
- Circuito medio sumador y circuito sumador completo
- Implementación de funciones booleanas mediante puertas lógicas
- Puerta OR exclusiva (puerta XOR)
- Símbolos lógicos para puertas lógicas básicas (O, Y, NO,…)
- Generador de paridad y verificación de paridad
Multiplexor (MUX) y multiplexación