En este tutorial, aprenderá cómo implementar funciones booleanas utilizando puertas lógicas. En el tutorial anterior, aprendimos sobre las leyes del álgebra booleana y teoremas relacionados. También aprendiste que las funciones booleanas se pueden expresar fácilmente en formato SOP (suma de productos) y POS (producto de sumas). Usamos puertas lógicas para representar lógicamente estas ecuaciones estandarizadas.
Cualquier función booleana se puede expresar utilizando una gran cantidad de puertas lógicas interconectándolas adecuadamente. La implementación de una puerta lógica o la representación lógica de una función booleana es una forma muy sencilla y sencilla.
La implementación de una función booleana utilizando puertas lógicas implica conectar la salida de una puerta lógica a la entrada de otra puerta. Las puertas lógicas más utilizadas son las puertas AND, OR, NAND y NOR.
Echemos un vistazo a las implementaciones de puertas lógicas de estilo SOP y POS de funciones booleanas.
Tabla de contenido
Una breve introducción a las puertas lógicas.
Las puertas lógicas son los componentes básicos de los circuitos electrónicos digitales. Las puertas lógicas son piezas de circuitos electrónicos que se pueden utilizar para implementar expresiones booleanas.
Las leyes y teoremas de la lógica booleana se utilizan para manipular expresiones booleanas, mientras que las puertas lógicas se utilizan para implementar estas expresiones booleanas en la electrónica digital.
La puerta Y, la puerta O y la puerta NO son tres puertas lógicas básicas utilizadas en la electrónica digital. Utilizando estas puertas lógicas básicas, se derivan otras puertas lógicas como NAND, NOR, OR exclusivo (Ex-OR) y NOR exclusivo (Ex-NOR).
Antes de ver la implementación de funciones booleanas usando puertas lógicas, repasemos rápidamente algunos conceptos básicos importantes de las puertas lógicas.
Y puerta
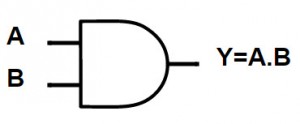
Una puerta lógica AND es una puerta lógica básica con dos o más entradas y una salida. La salida de una puerta AND es ALTA solo si todas las entradas de la puerta son ALTAS. La salida para todos los demás casos de entrada es BAJA. A continuación se muestran el símbolo lógico y la tabla de verdad de la puerta AND.
| a | B | Y = A y B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Si “A” y “B” son las dos entradas de una puerta AND, la expresión de salida se escribe como:
Y = A. B o Y = AB
Se lee como “Y IGUAL A A Y B”.
O puerta
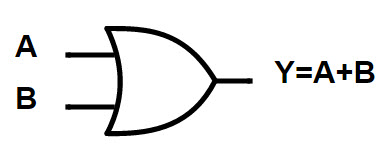
Las puertas OR se utilizan para realizar operaciones lógicas “OR”. Las puertas OR también tienen dos o más entradas y una salida. Si cualquiera de las entradas es ALTA, la salida de la puerta O será ALTA. Si todas las entradas están en BAJA, la salida será BAJA. A continuación se muestran el símbolo lógico y la tabla de verdad de la puerta OR.
| a | B | Y = A o B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Si ‘A’ y ‘B’ son las dos entradas de una puerta OR, la fórmula de salida se escribe como:
Y = A + B
Lea “Y es igual a A o B”.
no una puerta
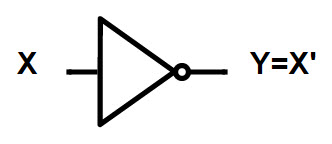
Una puerta lógica NOT es otra puerta lógica básica con una entrada y una salida. La salida de una puerta NOT es siempre el complemento de su entrada. Si la entrada es ALTA, la salida será BAJA; si la entrada es BAJA, la salida será ALTA. El símbolo lógico y la tabla de verdad de la puerta NOT se muestran a continuación.
| X | Y = X’ |
| 0 | 1 |
| 1 | 0 |
La puerta NOT se utiliza en álgebra booleana para generar el complemento de una variable. Por eso, también se le llama circuito complementario o inversor.
Implementación de funciones booleanas SOP mediante puertas lógicas
El formato de suma de productos o SOP se representa mediante las puertas lógicas básicas: puertas Y y O. La implementación del estilo SOP tiene una puerta AND en el lado de entrada y una puerta O en el lado de salida, ya que la salida de la función es la suma de todos los términos del producto.
Lo importante que debemos recordar es que usamos puertas NOT para representar el recíproco o complemento de una variable.
| Suma de productos (SOP) | |
| aporte | y |
| producción | o |
Implementación de dos variables de entrada
Entendamos cómo implementar las siguientes funciones booleanas utilizando puertas lógicas básicas.
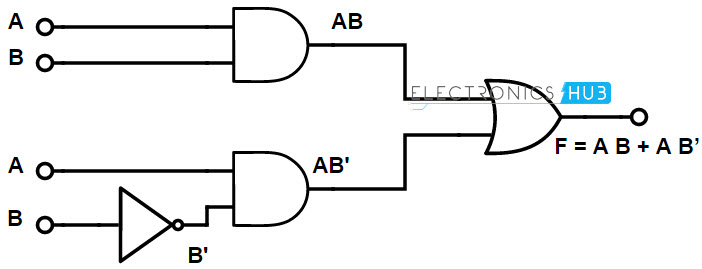
F = AB + A B
La función SOP especificada tiene un complemento. B. Por lo tanto, usamos una puerta NOT en el lado de entrada para representar la entrada complementaria. Y utilice una puerta AND para representar el término del producto. Consulte el diagrama lógico a continuación para ver la representación de funciones booleanas.
Implementando tres variables de entrada
Veamos cómo implementar la siguiente función booleana usando puertas lógicas básicas. Es una función de 3 variables de entrada.
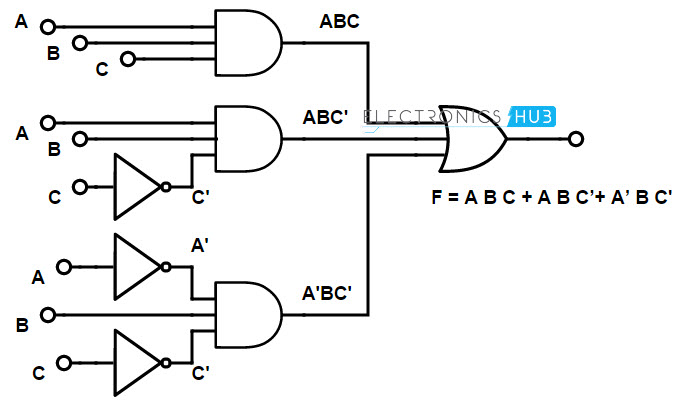
F = ABC + AB C + a B C
La función especificada tiene dos términos complementarios. a y C. Por lo tanto, usamos una puerta NOT en el lado de entrada para representar la entrada complementaria. Y utilice una puerta AND para representar el término del producto. Consulte el diagrama lógico a continuación para ver la representación de funciones booleanas.
Implementación de funciones booleanas de POS mediante puertas lógicas
El producto de sumas o forma POS se puede expresar utilizando puertas lógicas básicas como las puertas AND y OR. La implementación del formulario POS tiene una puerta O en el lado de entrada y una puerta Y en el lado de salida, ya que la salida de la función es el producto de todos los términos de la suma. Las implementaciones de formularios POS utilizan puertas NOT para representar el recíproco o el complemento de una variable.
| Producto de sumas (POS) | |
| aporte | o |
| producción | y |
Implementación de dos variables de entrada
Veamos cómo implementar la siguiente función booleana usando puertas lógicas básicas.
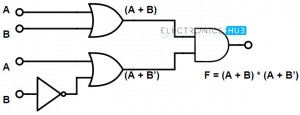
F = (A+B). (A+ B)
La función dada tiene un término complementario. B. Por lo tanto, usamos una puerta NOT en el lado de entrada para representar la entrada complementaria. Luego usamos una puerta OR para representar el término de suma. Consulte el diagrama lógico a continuación para ver la representación de funciones booleanas.
Implementando tres variables de entrada
Implemente funciones booleanas utilizando puertas lógicas básicas.
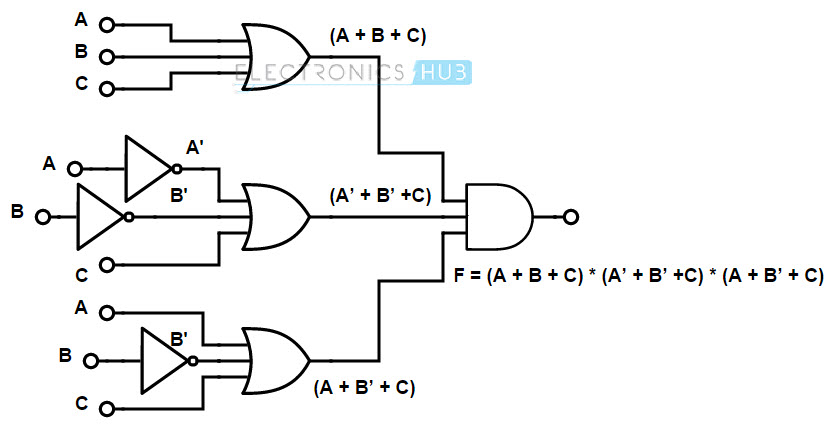
F = (A+B+C). (a + B +C). (A+ B +C)
La función booleana especificada tiene dos términos complementarios. a y B. Por lo tanto, usamos una puerta NOT en el lado de entrada para representar la entrada complementaria. Luego usamos una puerta OR para representar el término de suma. Consulte el diagrama lógico a continuación para ver la representación de funciones booleanas.
Implementación de funciones booleanas mediante puertas lógicas universales
Las puertas NAND y NOR se consideran “puertas lógicas universales”. La razón es que las puertas NAND y NOR pueden realizar (o funcionar de manera similar) las tres puertas básicas, como las puertas AND, OR y NOT. Puede diseñar puertas lógicas básicas utilizando puertas NAND o NOR. Por eso se la llama “puerta universal”.
Echemos un vistazo a la implementación de funciones booleanas utilizando puertas lógicas universales.
Implementación de funciones booleanas mediante puertas NAND
Una puerta NAND es una combinación lógica de una puerta AND y una puerta NOT, y funciona como una puerta AND, una puerta OR y una puerta NOT. Entonces usaremos puertas NAND para implementar la función booleana.
Lo importante que hay que recordar acerca de la puerta NAND es que es la inversa de la puerta AND básica. Esto significa que la salida de la puerta NAND es igual al complemento de la salida de la puerta AND.
Veamos un ejemplo para entender la implementación.
Implemente funciones booleanas utilizando puertas lógicas NAND.
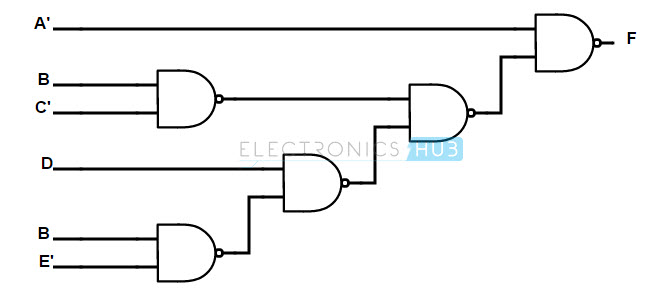
F (A, B, C, D, E) = A + (B + C) (D +Bmi)
La implementación de la puerta NAND utiliza puertas NAND tanto en el lado de entrada como en el de salida. Observe el diagrama lógico diseñado a continuación. A continuación se muestran instrucciones paso a paso para implementar una función booleana específica utilizando puertas NAND.
Primero, la función o ecuación booleana dada debe expresarse mediante una puerta AND-OR. La implementación de AND-OR se muestra a continuación.
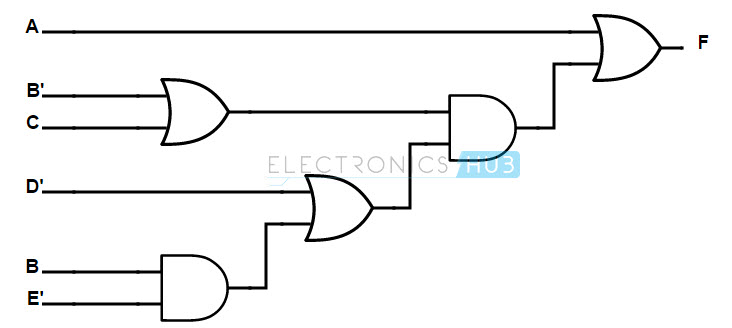
Para convertir una puerta AND en una puerta NAND, se introduce una burbuja (complemento) en la salida de la puerta AND. Para compensar la burbuja, también se introduce una burbuja en la entrada de la siguiente puerta. La implementación se muestra a continuación.
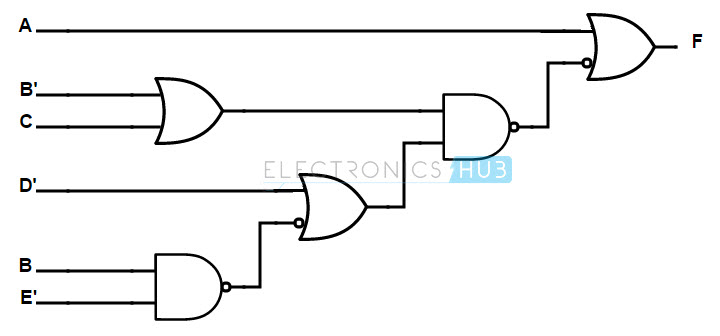
Para proporcionar uniformidad a las entradas, si una puerta tiene una entrada con una burbuja, también se introduce una burbuja en la otra entrada. Nuevamente, para compensar las burbujas, se introducen burbujas en la salida de la puerta anterior o se complementan con literales. Lo mismo se muestra en la siguiente figura.
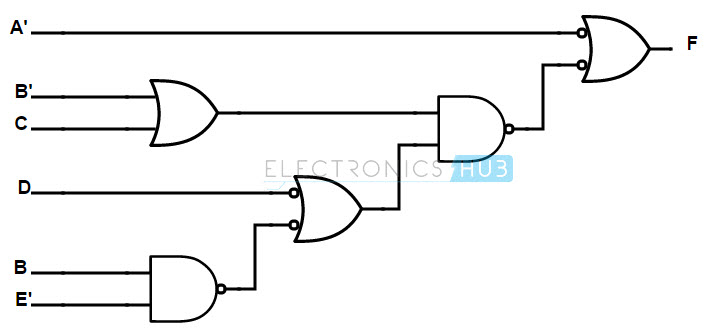
Si no hay ninguna burbuja en ninguna de las entradas de la puerta OR, se introducirá una burbuja y se corregirá adecuadamente como se muestra en la siguiente figura.
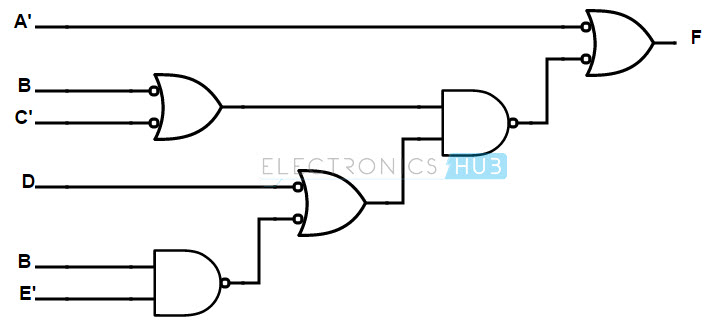
Una puerta OR con dos entradas complementarias equivale a una puerta NAND (según la ley de De Morgan A’+B’ = (AB)’). Por tanto, sustituyendo la puerta OR por dos entradas complementarias por una puerta NAND, obtenemos la estructura final de implementación de una función booleana utilizando puertas NAND. La implementación final se muestra a continuación.
Implementación de funciones booleanas mediante puertas NOR
Una puerta NOR es una combinación de una puerta O y una puerta NO, y funciona como una puerta Y, una puerta O y una puerta NO. Entonces implementaremos una función booleana usando una puerta NOR. Lo importante que hay que recordar acerca de la puerta NOR es que es la inversa de la puerta OR básica. Esto significa que la salida de la puerta NOR es igual al complemento de la salida de la puerta OR.
Veamos un ejemplo para entender la implementación.
Implemente una función booleana utilizando una puerta lógica NOR.
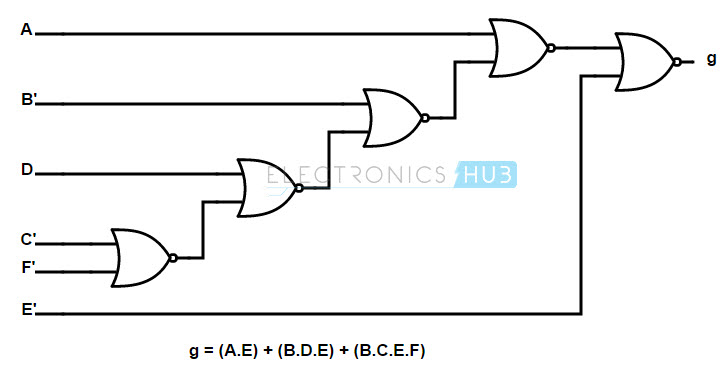
g (A, B, C, D, E, F) = (AE) + (BDE) + (BCEF)
La ecuación dada se puede reescribir como:
g (A, B, C, D, E, F) = AE + BDE + BCEF
= (A + BD + BCF) E
= (A + B (D + CF)) mi
La implementación de la puerta NOR utiliza puertas NOR tanto en el lado de entrada como en el de salida. Observe el diagrama lógico diseñado a continuación.
conclusión
Un tutorial completo para principiantes sobre la implementación de funciones booleanas utilizando puertas lógicas. Representación de ecuaciones con puertas lógicas (AND, OR, NOT), suma de productos (SOP) y suma de productos (POS) y su implementación usando puertas lógicas, e implementación de expresiones booleanas usando puertas universales (NAND y NOR) Aprendí los basicos. ).