Un multiplicador binario es un circuito lógico combinacional utilizado en sistemas digitales para realizar la multiplicación de dos números binarios. Se utilizan con mayor frecuencia para realizar diversos algoritmos en diversas aplicaciones, especialmente en el campo del procesamiento de señales digitales.
[adsense1]
Las aplicaciones comerciales como computadoras, dispositivos móviles, calculadoras de alta velocidad y algunos procesadores de uso general requieren multiplicadores binarios.
Comparada con la suma y la resta, la multiplicación es un proceso complejo. En la multiplicación, el número que se multiplica por otro número se llama multiplicando y el número que se multiplica se llama multiplicador.
Tabla de contenido
multiplicación binaria
Similar a la multiplicación decimal, la multiplicación binaria sigue el mismo proceso para producir el resultado del producto de dos números binarios. Multiplicar números binarios es mucho más fácil porque solo implica ceros y unos. Las cuatro reglas básicas de la multiplicación binaria son:
0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
La multiplicación de dos números binarios se puede realizar utilizando dos métodos comunes: suma y desplazamiento parcial de productos y uso de multiplicadores paralelos.
Antes de discutir los tipos, veamos el proceso de multiplicación binaria sin signo. Considerando dos números binarios de 4 bits, 1010 y 1011, la multiplicación de estos dos se obtiene como:
A partir de la multiplicación anterior, se genera un producto parcial para cada dígito del multiplicador. Todos estos productos parciales luego se suman para producir el valor del producto final. En la multiplicación de producto parcial, si el bit multiplicador es 0, el producto parcial es 0; si el bit multiplicador es 1, el producto parcial resultante es el multiplicando.
De manera similar a los números decimales, cada producto parcial sucesivo se desplaza un lugar hacia la izquierda con respecto al producto parcial anterior antes de sumar todos los productos parciales.
Por lo tanto, esta multiplicación utiliza n desplazamientos y suma n bits de números binarios. Los circuitos combinatorios implementados para realizar tales multiplicaciones se denominan multiplicadores de matriz o multiplicadores combinacionales.
Volver a la cima
[adsense2]
circuito multiplicador binario paralelo
Para generalizar el proceso de multiplicación, considere dos números binarios de 2 bits sin signo, A y B. El multiplicando A es igual a A1A0 y el multiplicador B es igual a B1B0. La siguiente figura muestra el proceso de multiplicar dos números binarios de 2 bits.
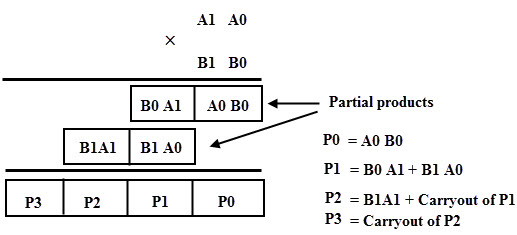
Este proceso implica multiplicar dos dígitos y sumar dígitos con o sin acarreo. Después de multiplicar cada bit por el multiplicando, se producen productos parciales y estos productos se suman para producir una suma que representa el valor binario multiplicado.
Como se muestra en la figura, esta multiplicación se logra usando un circuito combinacional que usa una puerta AND para la multiplicación y un medio sumador para la suma.
El primer producto parcial se obtiene mediante una puerta AND, que es sólo el bit menos significativo del resultado de la multiplicación. Dado que el segundo producto parcial se desplaza hacia la izquierda, el segundo término del producto parcial de la primera parte y el primer término del segundo producto parcial se suman en un medio sumador, lo que da la suma resultante junto con el resultado final.
Esta realización se agrega como entrada en el siguiente medio sumador como se muestra en la figura. De manera similar, encuentre el resultado de multiplicar dos números binarios usando una configuración de circuito simple. Al multiplicar dos números de 2 bits se obtiene un número binario de 4 bits.
Considere la multiplicación de dos números de 4 bits sin signo con el multiplicando A igual a A3A2 A1A0 y el multiplicador B igual a B3B2B1B0. Los productos parciales se generan dependiendo de cada bit multiplicador multiplicado por el multiplicando.
Cada producto parcial consta de cuatro términos de producto, que están desplazados hacia la izquierda con respecto al producto parcial anterior, como se muestra. Agregue todos estos productos parciales para producir un producto de 8 bits.
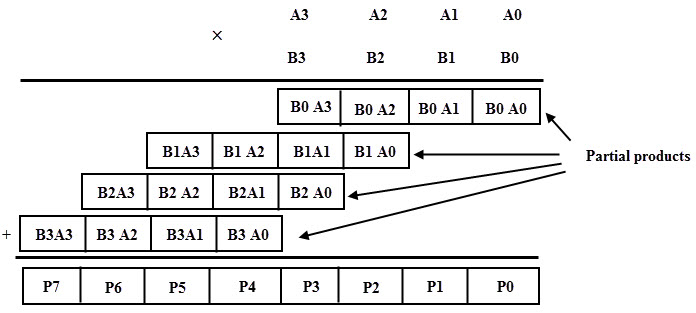
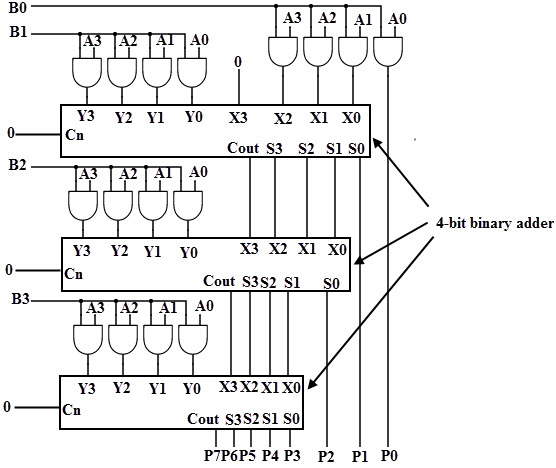
Se puede implementar un circuito lógico de multiplicación binaria 4×4 utilizando tres sumadores binarios completos y una puerta AND.
En la operación anterior, el primer producto parcial se obtiene multiplicando B0 y A3A2 A1A0, y el segundo producto parcial se forma multiplicando B1 y A3A2 A1A0, así como el tercer y cuarto producto parcial Masu. Por lo tanto, estos productos parciales se pueden implementar utilizando puertas AND como se muestra en la figura.
Estos productos parciales se suman mediante un sumador paralelo de 4 bits. Los tres bits más significativos del primer producto parcial con acarreo (que se supone cero) se suman con el segundo término parcial en el primer sumador completo.
Luego, el resultado se suma al siguiente producto parcial con arrastre, y así sucesivamente hasta el último producto parcial, produciendo finalmente una suma de 8 bits que representa el producto de los dos números binarios.
Volver a la cima
Multiplicador binario usando el método de cambio
En lugar del método automatizado anterior, se puede implementar un enfoque de multiplicación manual utilizando un sumador de n bits, cuatro registros (A, B, C, Q) y lógica de control y desplazamiento como se muestra en la siguiente figura.
En este caso, el multiplicador de 4 bits se almacena en el registro Q, el multiplicando de 4 bits se almacena en el registro B y el registro A primero se pone a cero. El proceso de multiplicación comienza verificando si el bit menos significativo de B es 0 o 1.
Si B0 = 1, el número del multiplicando (B) se suma con el bit menos significativo del registro A y todos los bits de los registros C, A y Q se desplazan un bit hacia la derecha.
Si el bit B0 = 0, los registros C y Q combinados se desplazan un bit hacia la derecha sin realizar una suma. Este proceso se repite n veces para n números de bits. Este método de multiplicación binaria se llama multiplicador paralelo.
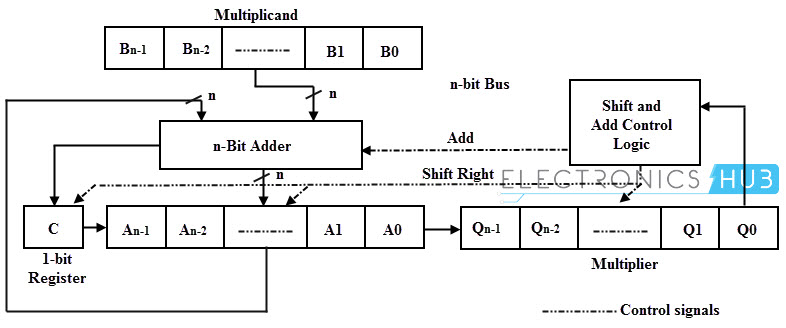
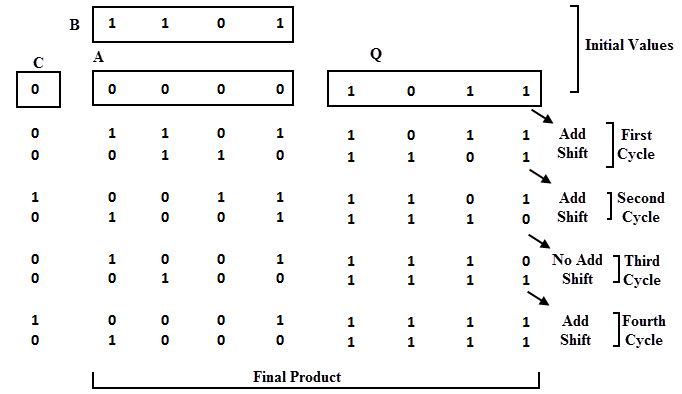
Considere el siguiente diagrama. Los valores de multiplicador y multiplicando se dan como 1011 y 1101 y se cargan en los registros Q y A, respectivamente. Inicialmente, el registro C es 0, por lo que el registro A también es 0 y se almacena un acarreo.
Como B0 = 1, el número en B se suma a los bits en A y el resultado de la suma es 1101. Los valores en los registros Q y A se desplazan un bit hacia la derecha, por lo que el nuevo valor en el primer ciclo es 0110. y 1101 respectivamente.
Para realizar una multiplicación de 4 bits, este proceso debe repetirse cuatro veces. El resultado final de la multiplicación se almacena en los registros A y Q como 10001111, como se muestra en la figura.
Un multiplicador binario sin signo de 4 × 4 toma dos entradas de 4 bits y produce una salida de 8 bits. De manera similar, un multiplicador de 8 × 8 acepta dos entradas de 8 bits y produce una salida de 16 bits.
Estos circuitos lógicos multiplicadores se implementan en circuitos integrados con varias configuraciones de pines.
Estos circuitos integrados se utilizan en una variedad de microprocesadores utilizados en diversas aplicaciones, especialmente computadoras, equipos de control, calculadoras, teléfonos móviles y procesadores de señales digitales (DSP).
Volver a la cima