descripción general
Tabla de contenido
¿Qué es el álgebra booleana?
El álgebra booleana es una rama especial del álgebra que se utiliza principalmente en electrónica digital. El álgebra de Boole fue inventada en 1854 por el matemático británico George Boole.
El álgebra booleana es una forma de simplificar circuitos lógicos (también conocidos como circuitos de conmutación lógica) en electrónica digital.
Por lo tanto, también se le llama “álgebra de cambio”. La funcionalidad de los circuitos lógicos se puede expresar numéricamente siguiendo una serie de reglas, bien conocidas como “leyes del álgebra de Boole”.
También puedes acelerar aún más los cálculos de circuitos y las operaciones lógicas siguiendo una serie de teoremas conocidos como “teoremas del álgebra de Boole”. Una función booleana es una función que representa la relación entre la entrada y la salida de un circuito lógico.
La lógica booleana permite sólo dos estados de un circuito, como Verdadero y Falso. Estos dos estados están representados por 1 y 0, donde 1 representa el estado “Verdadero” y 0 representa el estado “Falso”.
Lo más importante que hay que recordar sobre el álgebra de Boole es que el álgebra de Boole es muy diferente del álgebra matemática regular y sus métodos. Antes de aprender sobre el álgebra de Boole, conozcamos la historia del álgebra de Boole y su invención y desarrollo.
Historia del álgebra booleana
Como se mencionó anteriormente, el álgebra de Boole fue inventada en 1854 por el matemático británico George Boole. Describió por primera vez la idea del álgebra booleana en su libro “Una investigación sobre las leyes del pensamiento”.
Desde entonces, el álgebra de Boole se ha vuelto conocida como una forma perfecta de representar circuitos lógicos digitales.
A finales del siglo XIX, los científicos Jevons, Schroeder y Huntington modernizaron el concepto. Y en 1936, MHStone demostró que el álgebra de Boole es “isomorfa” con conjuntos (el dominio de las funciones en matemáticas).
En la década de 1930, el científico Claude Shannon desarrolló un nuevo tipo de técnica algebraica llamada “álgebra de conmutación” utilizando conceptos del álgebra de Boole para estudiar circuitos de conmutación.
La síntesis lógica en las herramientas modernas de automatización electrónica se expresa de manera eficiente mediante funciones booleanas conocidas como “diagramas de decisión binaria”.
El álgebra booleana permite sólo dos estados de circuitos lógicos: verdadero y falso, alto y bajo, sí y no, abierto y cerrado, 0 y 1.
expresión booleana
Son similares a las fórmulas. Las expresiones booleanas se forman combinando variables lógicas mediante operadores lógicos.Por ejemplo
- X+Y
- X+Y+XZ’
- X’+Y’
Postulados del álgebra booleana
Existen algunas leyes y reglas básicas que debe seguir un sistema de álgebra booleana. Se las conoce como las “leyes del álgebra booleana”.
Propiedades de 1 y 0
0 + X = X
1 + X = 1
0. X = 0
1.X = X
ley de identidad
X + 0 = X
X. 1 =X
ley idempotente
X + X = X
X. X=X
Supremacía o ley inválida
X.0 = 0
X + 1 = 1
Método de finalización
X + X’ = 1
X. X’ = 0
ley conmutativa
X + Y = Y + X
X. Y = Y.X
Ley distributiva
X.(Y + Z) = XY + XZ
X + (YZ) = (X + Y).(X + Z)
ley asociativa
X + (Y + Z) = (X + Y) + Z (o combinar)
X .(YZ) = (X . Y) Z (Asociación Y)
ley de absorción
X + XY = X (o absorción)
X .(X + Y) = X (y absorción)
Leyes de despido
X + X’.Y = X + Y
X.(X’ + Y) = XY
ley de combinación
X. Y + X. Y´=X
(X + Y) (X + Y’) = X
ley de involución
(X’)’ = X
ley del consenso
XY + X’.Z + YZ = XY + X’.Z
(X + Y).(X’ + Z).(Y + Z) = (X + Y).(X’ + Z)
| expresión booleana | explicación | circuito de conmutación equivalente | ley booleana |
|---|---|---|---|
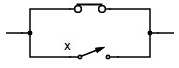
| X + 1 = 1 | Paralelo con X cerrado = “CERRADO” | abolición | |
| X + 0 = X | Abierto y paralelo X = “X” | 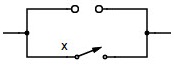 | identidad |
| X. 1 =X | Serie cerrada X = “X” | 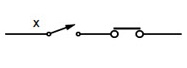 | identidad |
| X. 0 = 0 | X consecutiva y abierta = “ABIERTA” | 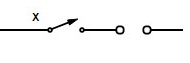 | abolición |
| X + X = X | X paralela a X = “X” | 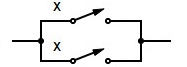 | idempotente |
| X. X=X | Serie de X (X = “X”) | 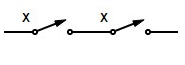 | idempotente |
| NO X’ = X | NO NO X (doble negativo) = “X” | doble negativa | |
| X + X’ = 1 | Paralelo X y NO X = “CERRADO” | 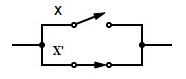 | complementar |
| X. X’ = 0 | secuencia de X con NOT X = “ABIERTO” | 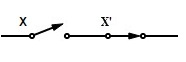 | complementar |
| X+Y = Y+X | X e Y paralelo =Y paralelo a X | 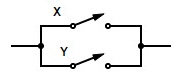 | conmutatividad |
| XY = YX | Serie de X e Y = Serie de Y y X | 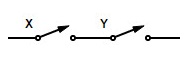 | conmutatividad |
| (X +Y)’ = X’.Y’ | Invierta el OR y reemplácelo con AND | teorema de morgan | |
| (XY)’ = X’+Y’ | Invertir AND y reemplazar con OR | teorema de morgan |
Operaciones lógicas booleanas
En matemáticas generales, los operadores aritméticos como +, -, * y / se utilizan para representar operaciones aritméticas entre variables algebraicas. De manera similar, el álgebra booleana utiliza operadores lógicos como las operaciones AND, OR y NOT para representar operaciones booleanas.
Hay tres tipos de operaciones aritméticas booleanas básicas. Estas son operación Y, operación O y operación NO. Las operaciones booleanas siempre se capitalizan.
Es incorrecto representar operaciones en minúsculas. Analicemos la aritmética booleana.
complemento (no es una función)
Complemento significa “valor inverso, recíproco u opuesto”. El álgebra de Boole apoya las leyes de complementariedad. Por ejemplo, si una variable es 1, su complemento es 0.
De manera similar, si una variable es 0, su complemento es 1. Las variables complementarias están representadas por una “barra” en la variable.
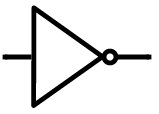
La operación complementaria también se llama operación NO. La puerta NOT realiza operaciones de complemento booleano.
Si X = 1, entonces X ̅ = 0
Si X = 0, entonces X ̅ = 1
La salida completa X ̅ se puede leer como X – barra o X – no. También representamos variables imputadas con un símbolo “primo” (‘), como X’.
El símbolo lógico para una puerta NOT se muestra a continuación.
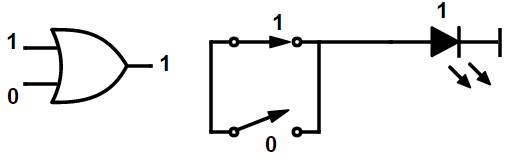
Suma (función O)
La función O significa suma booleana de números binarios. Produce la suma de dos números binarios como por ejemplo:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 1
La operación booleana OR se ilustra utilizando una puerta OR y contactos de interruptor paralelos.
Si 0 + 0 = 0
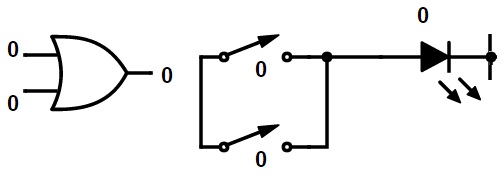
Si 0 + 1 = 1
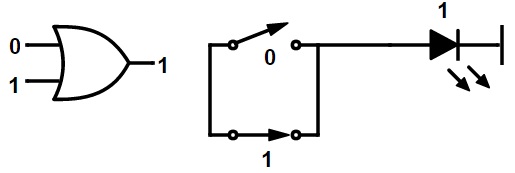
Si 1 + 0 = 1

Si 1 + 0 = 1
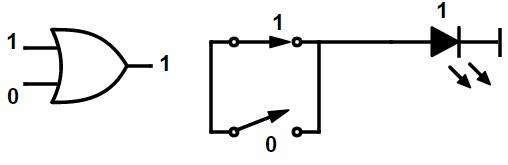
Si 1 + 1 = 1
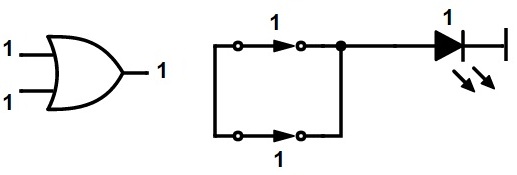
Lo importante que hay que recordar en el álgebra booleana es que no existe un mecanismo directo para sumar números negativos. Esto significa que la resta directa no es posible en el álgebra de Boole. La resta no es más que una “suma compleja”. Por ejemplo, 4 – 2 es lo mismo que 4 + (-2).
Multiplicación (función Y)
La función AND significa multiplicación booleana de números binarios. Produce el producto de dos números binarios, como por ejemplo:
0. 0 = 0
0. 1 = 0
1. 0 = 0
1. 1 = 1
La operación booleana AND se ilustra utilizando una puerta AND y contactos de interruptor en serie.
Si 0. 0 = 0

Si 0. 1 = 0
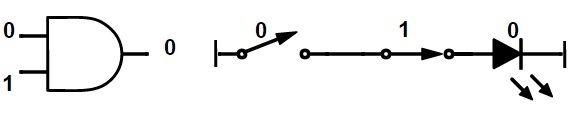
Alrededor de 1. 0 = 0
Alrededor de 1. 1 = 1

Lo importante que hay que recordar en el álgebra booleana es que no existe un mecanismo directo para dividir dos números. La división no es más que una “multiplicación compleja”.
Simplificando funciones booleanas
Los teoremas booleanos y las leyes booleanas se pueden utilizar para simplificar expresiones booleanas, reduciendo así la cantidad de puertas lógicas necesarias para la implementación. Puede simplificar funciones booleanas utilizando dos métodos.
- Método algebraico: utiliza identidades (leyes booleanas).
- Método gráfico: utilizando la proyección de Karnaugh
El método K-map es mucho más fácil para simplificar funciones que usar identidades. Si n es el número de variables, entonces el mapa K consta de 2n celdas y no hay valores similares en ninguna de las dos filas adyacentes de la columna.
Artículo relacionado:
- Símbolos lógicos para puertas lógicas básicas (O, Y, NO,…)
- Implementación de funciones booleanas mediante puertas lógicas
- Circuito medio sumador y circuito sumador completo
- Puerta OR exclusiva (puerta XOR)
- Generador de paridad y verificación de paridad
- Sumador binario y restador binario