resumen
Tabla de contenido
Introducción
Las resistencias son los componentes básicos de los circuitos eléctricos o electrónicos. A menudo, las resistencias se pueden encontrar en grandes cantidades independientemente del tamaño del circuito. Las resistencias se pueden conectar en serie, en paralelo o una combinación de ambas. Para reducir la complejidad de varias combinaciones de resistencias, se deben seguir una serie de reglas:
Se dice que dos resistencias están en serie cuando fluye la misma corriente. Una resistencia en serie puede ser reemplazada por una sola resistencia. Todas las resistencias obedecen leyes básicas, como la ley de Ohm y la ley actual de Kirchhoff.
Resistencias en serie
Se dice que un conjunto de resistencias está en serie si están conectadas espalda con espalda por un solo cable. La misma corriente fluye a través de todas las resistencias. Se dice que las resistencias en serie tienen una corriente común.
En una red resistiva en serie, la cantidad de corriente que fluye es la misma para todos.
YoR1 = IR2 = IR3 = IGrupo sanguíneo.
Considere el siguiente circuito resistivo en serie
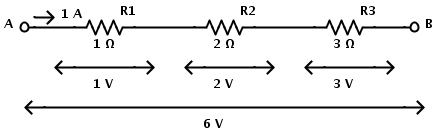
Aquí, las resistencias R1, R2 y R3 están conectadas en serie Ω 1 Ω, 2 Ω y 3, respectivamente. Dado que las resistencias están conectadas en serie, la misma corriente fluye a través de todas las resistencias. La resistencia total del circuito es igual a la suma de las resistencias individuales.
Si RT es el valor total de la resistencia, entonces
RT = R1 + R2 + R3
Ahora la resistencia equivalente del circuito es:
RIko = R1 + R2 + R3
RIko = 1 Ω + 2 Ω + 3 Ω
RIko = 6 Ω
Ahora puede reemplazar las resistencias en combinación en serie con una resistencia RIko Un valor de 6 Ω.
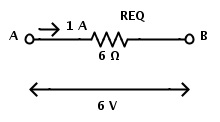
Resistencia equivalente
En una red de resistencia en serie, la misma corriente pasa a través de cada resistencia, por lo que la resistencia total es igual a la suma de las resistencias individuales.
∴Rtotal =R1 + Tecla R2 + Tecla R3
Por ejemplo, supongamos que tiene dos resistencias conectadas en serie, como se muestra a continuación
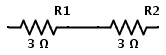
Conectar dos resistencias de tres Ω en serie equivale a tener una resistencia de seis Ω. Por lo tanto, el circuito anterior es el mismo que el siguiente
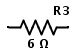
Del mismo modo, consideremos el caso en el que tres resistencias están conectadas en serie, como se muestra a continuación
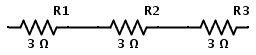
Conectar tres resistencias de tres Ω en serie equivale a tener una resistencia de nueve Ω. Por lo tanto, el circuito anterior es el mismo que el siguiente
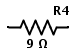
Esta resistencia única se denomina resistencia equivalente del circuito y se utiliza para reemplazar cualquier número de resistencias en serie.
Si hay n resistencias en la red en serie, entonces
RIko =R1 + Tecla R2 + Tecla R3 + ……..+ Rn
Se puede observar en la fórmula anterior. La resistencia equivalente de las resistencias conectadas en serie es siempre mayor que la resistencia de la resistencia más grande.
Calculadora de voltaje
En el caso de las resistencias en serie, el voltaje a través de cada resistencia no sigue las mismas reglas que la corriente. Cuando las resistencias están conectadas en serie, el voltaje total a través de las resistencias es igual a la suma de las diferencias de potencial individuales de cada resistencia.

En el circuito anterior, la diferencia de potencial de cada resistencia se puede calcular utilizando la ley de Ohm. Una corriente de 1 A fluye a través del circuito en serie. Entonces, de acuerdo con la ley de Ohm
La diferencia de potencial a través de la resistencia R1 es I×R1 = 1 × 1 = 1 V.
La diferencia de potencial a través de la resistencia R2 es I×R2 = 1 × 2 = 2 V.
La diferencia de potencial a través de la resistencia R3 es I×R3 = 1 × 3 = 3 V.
Por lo tanto, el voltaje total VGrupo sanguíneo = 1V + 2V + 3V = 6V.
Considere la conexión en serie de tres resistencias R1、R2 y R3 Con una corriente eléctrica, los atravieso.

Sea V la caída potencial de A a B. Esta caída potencial es la suma de las caídas potenciales individuales de las resistencias individuales. A continuación, cumpla con la ley de OHM de CA
Disminución potencial de la R general1 VR1 = I × R1
Disminución potencial de la R general2 VR2 = I×R2
Disminución potencial de la R general3 VR3 = I×R3
∴ V = VR1 + VR2 + VR3
∴V = I × R1 + Yo × R2 + Yo × R3
La resistencia equivalente de las resistencias conectadas en serie en el circuito anterior es RIkoEntonces
V = I × RIko
Serie R1, R2…. Si Rn tiene n resistencias, entonces el voltaje total a través de ellas es la suma de las diferencias de potencial individuales entre cada resistencia.
VT =VR1 + VR2 + …..+ VRn
En una combinación de resistencias en serie de n resistencias, si el valor de resistencia de cada resistencia es diferente del valor de las demás, el potencial a través de cada resistencia será diferente.
N resistencias en combinación en serie, cada una con una resistencia diferente, tendrán N diferencias de potencial diferentes entre ellas. Este tipo de circuito forma un divisor de voltaje. El circuito divisor de voltaje es la base de la estructura del potenciómetro.
En un circuito en serie, el valor del voltaje, la corriente o la resistencia se puede calcular utilizando la ley de Ohm. Las resistencias se pueden reemplazar en un circuito en serie sin afectar la potencia total, la corriente o la resistencia total del circuito a cada resistencia.
Ejemplo de una resistencia en serie
1. Para calcular el voltaje total entre A y B, considere el siguiente circuito:
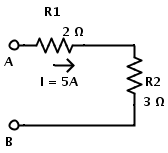
Las dos resistencias, R1 y R2, están conectadas en serie.
R1 = 2 Ω y R2 = 3 Ω
La corriente en el circuito es I = 5A.
Las caídas de tensión individuales se pueden calcular utilizando la ley de Ohm de la siguiente manera:
La caída de voltaje a través de la resistencia R1 es VR1 = I × R1 = 5 × 2 = 10V
La caída de voltaje a través de la resistencia R2 es VR2 = I × R2 = 5 × 3 = 15V
La caída de tensión total es la suma de las caídas de tensión individuales.
V = VR1 + VR2 = 10 + 15 = 25V
Otro enfoque consiste en calcular la resistencia equivalente de la combinación de series. Las resistencias individuales en combinaciones en serie pueden ser reemplazadas por una sola resistencia de resistencia equivalente. La resistencia equivalente de dos resistencias R1 y R2 en serie viene dada por:
RIko =R1 + Tecla R2 = 2 + 3 = 5Ω
Entonces, de acuerdo con la ley de Ohm,
La caída de voltaje a través de A y B es
V = I × RIko = 5 × 5 = 25V.
- Considere el siguiente circuito, en el que se dan los valores de las caídas de potencial individuales a través de cada resistencia junto con las corrientes combinadas en serie. La resistencia total de las combinaciones de series se da como R = 30 Ω. La corriente en el circuito es de 1A.
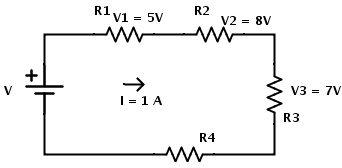
R = 30 Ω e I = 1 A
La corriente que fluye a través de cada resistencia es la misma.
I = I1 = I2 = I3 = I4 = 1A.
De acuerdo con la ley de Ohm, el valor de la resistencia se puede calcular de la siguiente manera:
R1 =V1 /Yo1
R1 = 5 / 1 = 5Ω
Del mismo modo, R2 =V2 /Yo2
R2 = 8 /1 = 8Ω
y R3 =V3 /Yo3
R3 = 7 / 1 = 7Ω
El potencial de R en su conjunto4 no se especifica. Sin embargo, el valor de R4 Se puede calcular a partir del valor de la resistencia total o equivalente del circuito.
RIko =R1 + Tecla R2 + Tecla R3 + Tecla R4
∴R4 =RIko– (R1 + Tecla R2 + Tecla R3)
R4 = 30 – (5 + 8 + 7)
R4 = 10Ω
Esto abre las posibilidades para todo el R4 Se puede calcular de la siguiente manera:
V4 = I4 ×R4
∴V4 = 1 × 10 = 10V
Tensión total VGrupo sanguíneo se puede calcular de dos maneras.
El primer método consiste en utilizar diferencias de potencial individuales.
El voltaje total es igual a la suma de las diferencias de potencial individuales.
VGrupo sanguíneo =V1 + V2 + V3 + V4
donde V1, V2, V3 y V4 son las diferencias de potencial de las resistencias R1, R2, R3 y R4, respectivamente.
Por lo tanto, VGrupo sanguíneo = 5 + 8 + 7 + 10
VGrupo sanguíneo = 30 V
La segunda forma de calcular el voltaje total es usar el valor de la resistencia equivalente.
El voltaje total es igual al producto de la corriente y la resistencia equivalente. El valor de la corriente total y la resistencia equivalente se da como I = 1 A y RIko = 30 Ω.
Por lo tanto, VGrupo sanguíneo = I × RIko
VGrupo sanguíneo = 1 × 30
VGrupo sanguíneo = 30 V
aplicación
Cuando dos resistencias con diferentes resistencias están conectadas en serie, el voltaje a través de ellas es diferente. Este método es la base del circuito divisor de voltaje.
Cuando la resistencia en el circuito divisor de voltaje se reemplaza con un sensor, la cantidad a detectar se convierte en una señal eléctrica que se puede medir fácilmente. Los sensores más utilizados son los termistores y las resistencias dependientes de la luz. En los termistores, el valor de resistencia cambia con la temperatura. Por ejemplo, supongamos que el termistor tiene una temperatura de 25 y una resistencia de 10 KΩ0C. El mismo termistor puede tener una resistencia de 100 Ω a una temperatura de 1000Por lo tanto, la caída de potencial a través del termistor depende de la temperatura. El cambio en la resistencia debido a esta temperatura se puede calibrar para determinar el valor de temperatura a partir de la caída de potencial a través del termistor.
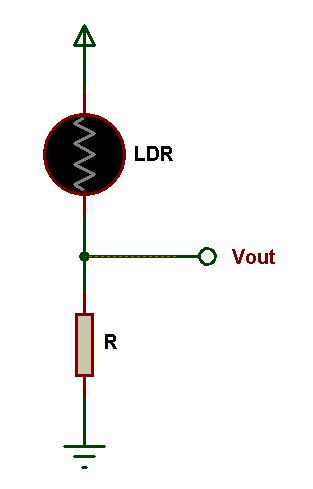
Figura: Circuito del fotosensor
Otro sensor que utiliza resistencias en serie es una fotorresistencia o una resistencia dependiente de la luz. En las resistencias dependientes de la luz, la resistencia varía en función de la intensidad de la luz incidente. En ausencia de luz, la resistencia de una resistencia estándar dependiente de la luz puede ser tan alta como 1 MΩ. En presencia de luz, la resistencia de las resistencias dependientes de la luz generalmente cae a valores pequeños del orden de unos pocos ohmios. La caída de voltaje se puede calibrar para encontrar la presencia de una longitud de onda de luz específica.
Artículos Relacionados:
- Circuitos en serie |Conceptos básicos, características,…
- Series y paralelos |
- Circuitos Paralelos | Conceptos Básicos, Ecuaciones, Voltaje, Corriente
- Conoce los diferentes tipos de circuitos…
- Fundamentos de funcionamiento de los potenciómetros, símbolos, aplicaciones, cono
- Amplificador operacional no inversor |

