Introducción a los filtros y reactores capacitivos

Introducción

Un filtro eléctrico es un circuito diseñado para eliminar todos los componentes de frecuencia no deseados de una señal eléctrica y permitir solo las frecuencias necesarias. En otras palabras, un filtro es un circuito que permite solo una determinada banda de frecuencia. El uso principal de los filtros es en ecualizadores de audio y electrónica sensible donde la señal de entrada debe ser condicional. Estos filtros se dividen en dos tipos principales: Se trata de filtros activos y pasivos.

Filtros pasivos

Un filtro pasivo no contiene un elemento amplificador, sino que consta de una resistencia, un condensador y un inductor (componente pasivo). Estos filtros no consumen energía adicional de la energía de la batería externa. Los condensadores permiten señales de alta frecuencia, mientras que los inductores permiten señales de baja frecuencia. De manera similar, un inductor restringe el flujo de señales de alta frecuencia, mientras que un condensador restringe las señales de baja frecuencia. En estos filtros, la amplitud de la señal de salida es siempre menor que la amplitud de la señal de entrada aplicada. La ganancia de un filtro pasivo es siempre inferior a uno. Esto indica que la ganancia de la señal no se puede mejorar con estos filtros pasivos. Por esta razón, las características del filtro se ven afectadas por la impedancia de carga. Estos filtros también funcionan en el rango de alta frecuencia cercano a los 500 MHz.

Filtros activos

Además de los componentes pasivos (resistencias, condensadores e inductores), los filtros activos incluyen elementos amplificadores (componentes activos) como amplificadores operacionales, transistores y FET. Mediante el uso de estos filtros, puede superar las deficiencias de los filtros pasivos. El filtro activo se basa en una fuente de alimentación externa para amplificar la señal de salida. Incluso sin un elemento inductor, estos pueden alcanzar la frecuencia de resonancia, que es la impedancia de entrada, y la impedancia de salida es mutuamente inválida. Los inductores del año siguiente tenían un diseño sin filtro. Esto se debe a que el inductor consume una cierta cantidad de energía y genera un campo magnético parásito. Además de estos problemas, el inductor hace que el filtro activo aumente de tamaño. Por lo tanto, por estas razones, se reduce el uso de inductores en filtros activos.

Algunas de las ventajas de los filtros activos

• La combinación de amplificadores operacionales, resistencias, condensadores, transistores y FET forma un circuito integrado que reduce el tamaño y el peso del filtro.
• La ganancia del amplificador operacional se puede controlar fácilmente en bucle cerrado. Debido a esto, la señal de entrada no está restringida.
• Estos se pueden aplicar a los filtros Butterworth, Chebyshev y Kauer.

La principal desventaja de los filtros activos es su estrecho rango de frecuencia de funcionamiento. En muchas aplicaciones, el rango de frecuencia de funcionamiento del filtro activo se maximiza a 500 kHz. El filtro activo requiere una fuente de alimentación de CC. En comparación con los filtros pasivos, estos filtros activos son más sensibles. Además, la salida puede verse alterada por cambios en el entorno.

El filtro es un circuito sensible y el componente de salida es solo el término de frecuencia. La mejor manera de analizar los circuitos de filtro es utilizar una representación en el dominio de la frecuencia. La expresión es la siguiente:

La magnitud del filtro M se denomina ganancia del filtro. La amplitud suele expresarse en dB como 20log (M).

Una de las características importantes del filtro es la frecuencia de corte. Se define como la frecuencia que separa la banda de paso de la banda de parada en la respuesta de frecuencia. La banda de paso es el rango de frecuencias que permite el filtro sin atenuación. La banda de parada se define como una banda de frecuencia que no está permitida por el filtro.

Los filtros se clasifican en función de la frecuencia de la señal por la que puede pasar el filtro. Hay cuatro tipos de filtros: filtros de paso bajo, filtros de paso de banda, filtros de paso alto y filtros de paso de banda. Debido al uso de amplificadores operacionales de alta velocidad, los valores de los componentes, las características de la respuesta ideal y la respuesta real son casi las mismas.

Filtro de paso bajo

Un filtro de paso bajo pasa una señal de frecuencia inferior a la frecuencia de corte “fc”. En la práctica, incluso después del rango de frecuencia de corte, pasa un pequeño rango de frecuencias. La ganancia del filtro depende de la frecuencia. A medida que aumenta la frecuencia de la señal de entrada, la ganancia del filtro disminuye. Al final de la banda de transición, la ganancia es cero. Esto se muestra a continuación.

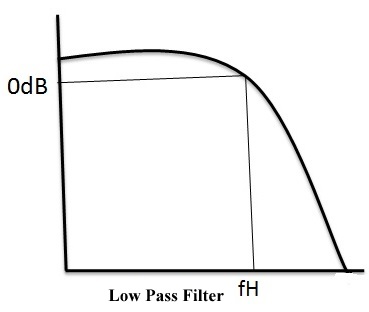
Figura: Paso bajo 1

Aquí, la línea punteada indica las características ideales del filtro, y la línea continua indica las características prácticas del filtro.

La aplicación de los filtros de paso bajo es en sistemas de sonido que se instalan en varios tipos de altavoces. Para bloquear la radiación armónica, estos filtros de paso bajo se utilizan en transmisores de radio. También se utilizan en divisores DSL en líneas telefónicas de abonado.

Filtro de paso alto

Pase la frecuencia después de la frecuencia de corte “fc”. En la práctica, el filtro tolera frecuencias insignificantes por debajo del rango de corte. Esto se muestra a continuación.

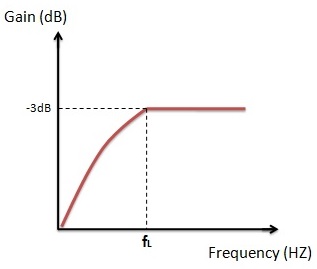
Figura: Paso alto 1

La combinación de filtros de paso alto y paso bajo forma un filtro de paso de banda. Los filtros de paso alto se utilizan en circuitos de RF y también se utilizan en divisores DSL.

Filtros de paso de banda

El propio nombre del filtro indica que solo permite ciertas bandas de frecuencia y bloquea todas las demás. Los límites superior e inferior de un filtro de paso de banda dependen del diseño del filtro. A continuación se muestran las características prácticas e ideales de los filtros de paso de banda.

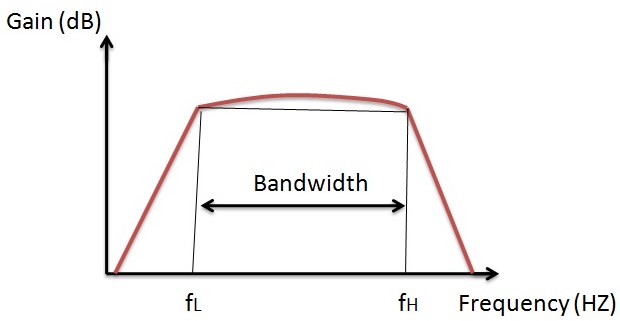
Figura: Paso de banda 1

Los filtros de paso de banda se utilizan en circuitos transmisores y receptores. Se utilizan principalmente para calcular la sensibilidad del circuito receptor y optimizar la relación señal-ruido.

Filtro de parada de banda

Estos también se conocen como filtros de eliminación de banda o filtros de eliminación de banda. Estos filtros detienen solo ciertas bandas de frecuencia y permiten todas las demás frecuencias. El límite de frecuencia del filtro depende del diseño del filtro. La línea punteada indica el caso ideal, y la línea continua indica el caso práctico. Tiene dos bandas de paso y una banda de parada.

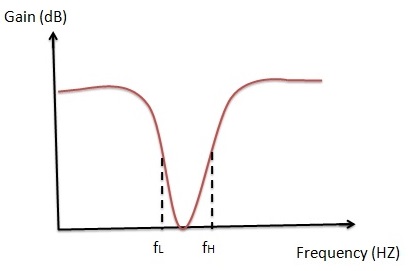
Figura: Parada de banda 1

Los filtros de parada de banda se utilizan en amplificadores de instrumentación.

Respuesta en frecuencia de un filtro ideal

Ahora, echemos un vistazo a la respuesta ideal de los diferentes filtros. donde fL indica una frecuencia de corte baja y fH indica una frecuencia de corte alta.

Características ideales de los filtros de paso bajo

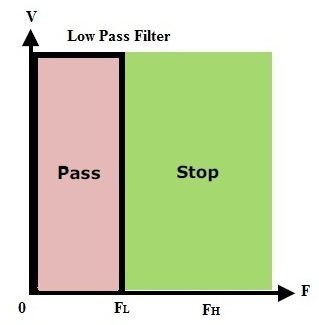
Figura: Paso bajo 2

Esta respuesta indica que el filtro de paso bajo tolera la señal a una frecuencia de corte más baja y detiene las frecuencias más altas que la frecuencia de corte más baja.

Características ideales de los filtros de paso alto

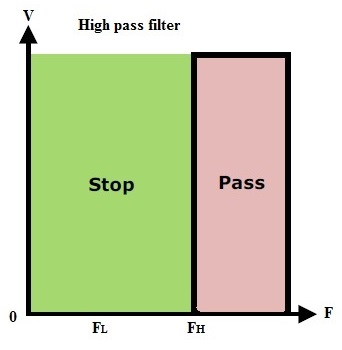
Figura: Paso alto 2

Esto indica que el filtro de paso alto permite frecuencias más altas que la frecuencia de corte alta y detiene frecuencias más bajas que la frecuencia de corte alta.

Características ideales de los filtros de paso de banda

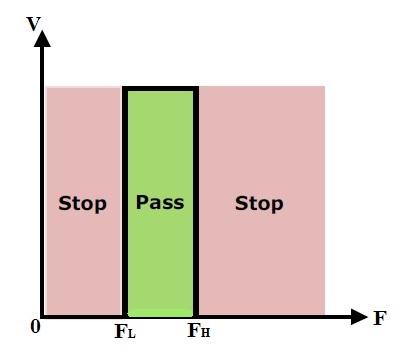
Figura: Paso de banda 2

Esta respuesta indica que el filtro de paso de banda pasa solo las frecuencias entre las regiones de corte inferior y superior. Detiene las frecuencias que son más bajas que la frecuencia de corte más baja y también detiene las frecuencias que son más altas que la frecuencia de corte alta.

Características ideales de los filtros de parada de banda

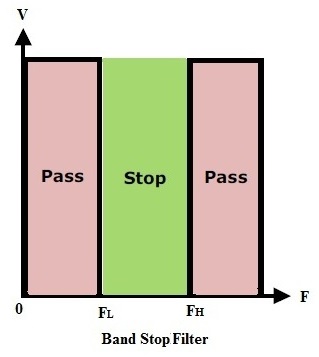
Figura: Parada de banda 2

La figura anterior muestra que las frecuencias superiores a las frecuencias de corte inferiores y las frecuencias inferiores a las frecuencias de corte altas no se procesan.

Reactancia capacitiva

Cuando la resistencia se conecta en serie con el condensador, forma un circuito RC. En los circuitos RC, el condensador se carga desde el voltaje de la fuente de alimentación de CC, y cuando el voltaje de la fuente de alimentación disminuye, el condensador eventualmente también reducirá la carga y descarga almacenadas. No solo cuando la fuente de alimentación es de CC, sino también cuando el condensador es alimentado por una fuente de alimentación de CA, el condensador se carga y descarga continuamente de acuerdo con el nivel de voltaje de la fuente de alimentación.

Sin embargo, debido a la resistencia interna, la corriente que fluye a través del condensador se atenúa un poco. Esta resistencia interna se denomina reactancia capacitiva. ‘X_C’ indica la reactancia capacitiva, que se mide en ohmios igual a la resistencia.

Cuando se cambia la frecuencia en un circuito capacitivo de acuerdo con la cantidad de cambio de frecuencia, este valor de reactancia capacitiva también cambia. Cuando los electrones fluyen de una placa a otra, una corriente eléctrica fluye a través del circuito. Sin embargo, debido al movimiento de los electrones, el nivel de frecuencia s cambia. A medida que aumenta la frecuencia a través del condensador, el valor de reactancia capacitiva disminuye, y a medida que disminuye la frecuencia a través del condensador, aumenta el valor de reactancia capacitiva. Por lo tanto, podemos decir que la reactancia capacitiva es inversamente proporcional al nivel de frecuencia aplicado. Esto indica que el condensador conectado al circuito depende de la frecuencia de alimentación. Este fenómeno se denomina impedancia compleja.

capacitivade reactancia

X_c = 1/(2π1c)

Donde: X_c = Reactancia capacitiva

π = 3.142

f = Frecuencia (Hz)

c = Capacitancia del faradio (F).

Ejemplo de reactancia capacitiva

Para observar el fenómeno de la reactancia capacitiva, consideremos dos frecuencias. Supongamos que f_1 = 1kHzandf_2 = 10 kHz y el condensador c = 220 nF.

Primer nivel de frecuencia

X_C= 1/2πf1c = 723.4Ω

En el segundo nivel de frecuencia, se ve así:

X_C= 1/2πf2c= 72.34Ω

Esta es una clara indicación de que la reactancia disminuye con el aumento de la frecuencia.

Reactancia capacitiva vs. frecuencia

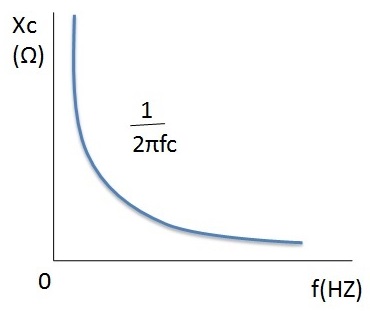
A partir de los gráficos de frecuencia y reactancia capacitiva anteriores, se puede observar que cuando la frecuencia es cero, el valor de reactancia alcanza el infinito, lo que indica el fenómeno de un circuito abierto. A medida que el valor de la frecuencia aumenta exponencialmente, el valor de reactancia disminuye. Cuando la frecuencia alcanza el infinito, el valor de reactancia es casi cero, lo que da como resultado un funcionamiento en circuito cerrado.

Concepto de divisor de tensión

Ya ha aprendido el concepto de divisor de voltaje en el tema de las resistencias, y sabe que un circuito divisor de voltaje puede producir un voltaje de salida que es solo una fracción del voltaje de entrada.

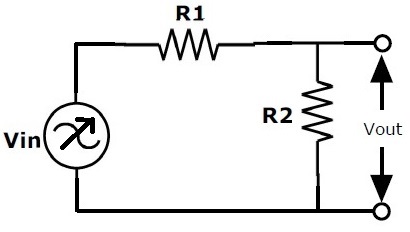
V_fuera =V_Y x (R₂ / (R₁ + Tecla R₂))

Si la resistencia R2 se reemplaza por un condensador C en el circuito anterior, la caída de voltaje entre los dos componentes variará con la frecuencia de entrada, porque la reactancia del condensador cambiará con la frecuencia. El voltaje de salida a través del condensador ahora depende de la frecuencia de entrada. Usando este concepto, se pueden construir filtros pasivos de paso bajo y paso alto reemplazando una de las resistencias en el circuito divisor de voltaje con un condensador.

Comportamiento del condensador en un filtro de paso bajo.

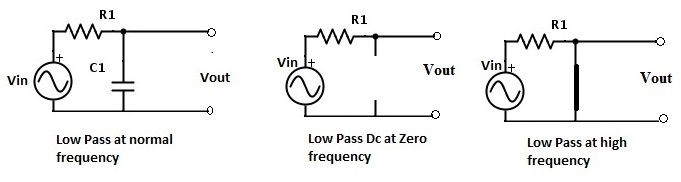
En el caso de un filtro de paso bajo, la resistencia R2 se sustituye por el condensador C1. A frecuencias normales, el circuito se parece a la figura anterior. Cuando la frecuencia es cero, el valor de reactancia es muy alto y es aproximadamente igual a infinito. En este estado, el circuito actúa como un circuito abierto. Si la frecuencia es muy alta, el valor de reactancia llega a cero y el circuito actúa como un circuito cerrado. Ambos comportamientos se ilustran en el diagrama anterior.

Comportamiento del condensador de un filtro de paso alto

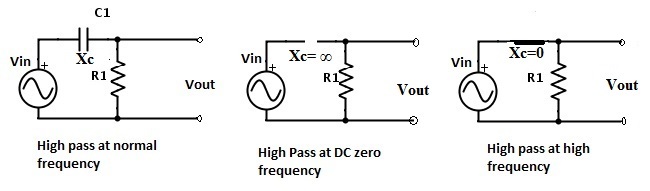
En el caso de un filtro de paso alto, la resistencia R1 se sustituye por el condensador C1. En el diagrama anterior, está claro que a frecuencias normales, el circuito se comporta como un circuito de filtro de paso alto. En el estado inicial, a valores de frecuencia cero, el circuito se comporta como un circuito abierto. A medida que aumenta la frecuencia, la reactancia disminuye exponencialmente. En algún momento, la frecuencia alcanza el nivel infinito, lo que afecta a la reactancia para alcanzar el estado cero. El funcionamiento de estos circuitos se muestra en la figura anterior.