resumen
Tabla de contenido
Definición de diferencia de potencial
[adsense1]
Considere la tarea de mover una carga eléctrica de A a B con un campo eléctrico uniforme. Hagamos que este movimiento vaya en contra del campo eléctrico. La fuerza externa realiza algún trabajo sobre esta carga, y este trabajo cambia la energía potencial a un valor más alto. La cantidad de trabajo realizado es igual al cambio en la energía potencial. Este cambio en la energía potencial crea una diferencia de potencial entre los dos puntos A y B. Esta diferencia de potencial se denomina diferencia de potencial y se mide en voltios (V).
La diferencia de potencial se expresa en ∆ V y se define como la diferencia de potencial o tensión entre dos puntos.
Si VA es el potencial de A y VB es el potencial de B, entonces a partir de la definición de la diferencia de potencial,
∆VBA = VB – VA
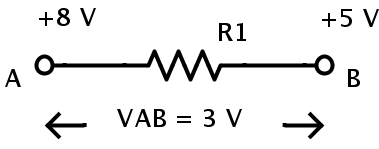
Por ejemplo, considere la siguiente resistencia, R1:
[adsense2]
El potencial aplicado a un extremo de la resistencia (punto A) es de 8 V, y el potencial aplicado al otro extremo de la resistencia (punto B) es de 5 V.
La diferencia de potencial entre dos puntos A y B es
VAB = 8 – 5 = 3 V.
Esto también se conoce como potencial a través de la resistencia.
La corriente eléctrica fluye a través de los circuitos eléctricos en forma de cargas eléctricas, mientras que los potenciales eléctricos no fluyen ni se mueven. Se aplica una diferencia de potencial entre los dos puntos.
La unidad de diferencia de potencial entre dos puntos son los voltios. Un voltio se define como la caída de potencial a través de una resistencia de 1 ohmio (Ω) a través de la cual fluye una corriente de 1 amperio.
por consiguiente
1 voltio = 1 amperio × 1 ohmio
V = I × R
De acuerdo con la ley de Ohm, la corriente que fluye a través de un circuito lineal es directamente proporcional a la diferencia de potencial en todo el circuito. Por lo tanto, cuanto mayor sea la diferencia de potencial aplicada al circuito, mayor será la corriente que fluye a través del circuito.
Por ejemplo, si el potencial en un lado de una resistencia de 1 Ω es de 8 V y el otro lado es de 2 V, la diferencia de potencial a través de la resistencia es de 5 V. La corriente que fluye a través de la resistencia es
I = V / R = 5V / 1 Ω = 5 amperios.
Para la misma resistencia de 1-Ω, supongamos que desea aumentar el potencial aplicado en un extremo de 8 V a 12 V y el potencial aplicado en el otro extremo de 2 V a 4 V. En este caso, la diferencia de potencial a través de la resistencia será de 8 V. En esta situación, la corriente que fluye a través de la resistencia es de 8 amperios.
I = V / R = 8V / 1 Ω = 8 amperios.
En general, en los circuitos eléctricos, el bajo potencial es tierra o tierra. Por lo general, se considera que este valor es de 0 V y la diferencia de potencial es igual al voltaje aplicado. La Tierra se considera el punto común del circuito. Esta referencia de tierra o tierra como punto común de los circuitos eléctricos ayuda a facilitar la comprensión del circuito. La diferencia de potencial también se denomina voltaje.
Los voltajes conectados en serie se suman para obtener el voltaje total en el circuito. Esto se puede observar con resistencias conectadas en serie. Si V1, V2 y V3 están conectados en serie, el voltaje total VT viene dado por:
VT = V1 + V2 + V3.
En el caso de elementos conectados en paralelo, el voltaje entre ellos será igual. Esto se puede observar en las resistencias en el tutorial paralelo.
VT = V1 = V2 = V3.
Ejemplo de diferencia de potencial
- Al transferir 1500 julios de energía potencial para transferir una carga de 125 culombios entre los terminales de la batería, la diferencia de potencial será:
∆E = 1500 J
Q = 125°C
Diferencia potenciométrica V = ∆E/C
V = 1500 / 125 = 12 julios / Coulomb = 12 V
2. Considere una resistencia de 10 Ω. Conecte un extremo de la resistencia a un potencial de 15 V. Conecte el otro extremo de la resistencia a un potencial de 5V. La corriente que fluye a través de la resistencia se puede calcular de la siguiente manera:
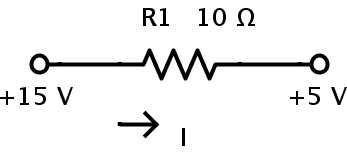
Los dos terminales de la resistencia están ubicados en dos potenciales diferentes, 15 V y 5 V, respectivamente. Los dos terminales son A y B. Por lo tanto, el voltaje de A es VA = 15 V y el voltaje de B es VB = 5 V. A su vez, la diferencia de potencial entre A y B es el voltaje a través de la resistencia.
VAB = VA – VB = 15 – 5 = 10 V.
La corriente que fluye a través de la resistencia se puede calcular utilizando la ley de Ohm de la siguiente manera:
I = VAB / R = 10 / 10 = 1 amperio.
Circuito divisor de voltaje
Las isostas con una conexión en serie de grados de resolución se utilizan para generar circuitos divisores de tensión. Un divisor de voltaje es un circuito lineal en el que el voltaje de salida es solo una fracción del voltaje de entrada.
A continuación se muestra un circuito divisor de voltaje simple con dos resistencias.
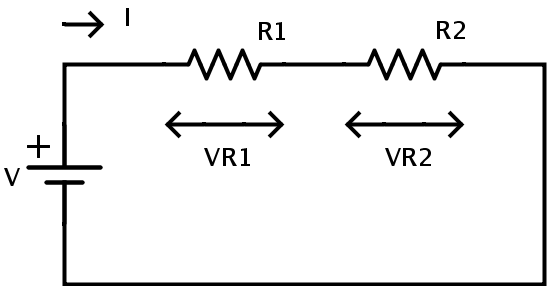
El potencial a través de cada resistencia en conexión en serie depende del valor de la resistencia. El principio del divisor de voltaje es producir un voltaje que sea una fracción del voltaje de entrada.
El siguiente circuito se utiliza para ilustrar el principio de un divisor de voltaje para múltiples voltajes de salida.

Aquí, las resistencias R1, R2, R3 y R4 están conectadas en serie. El voltaje de salida a través de cada resistencia está referenciado al punto común P. Sea RT la resistencia equivalente de la resistencia en serie. Entonces RT = R1 + R2 + R3 + R4.
Sea V la diferencia de potencial entre cada resistenciaR1 、VR2 、VR3 y VR4 Para R1, R2, R3 y R4, respectivamente. A su vez, el circuito anterior puede generar cuatro voltajes diferentes, que son fracciones del voltaje de alimentación V.
divisor de tensión
El valor de la tensión de salida de un circuito divisor de tensión típico se calcula de la siguiente manera:
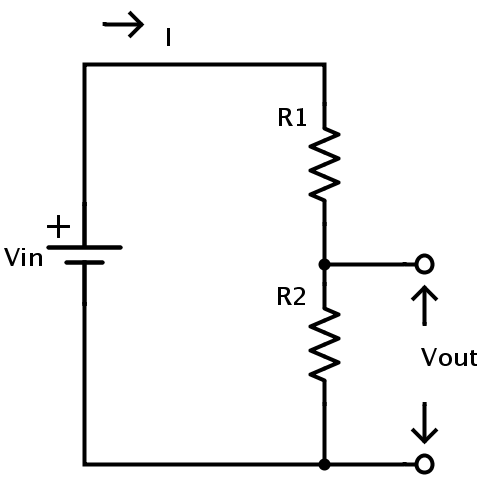
donde Vin es el voltaje de alimentación. I es la corriente en el circuito que fluye a través de ambas resistencias.
Sea VR1 la caída de voltaje a través de la resistencia R1 y VR2 sea la caída de voltaje a través de la resistencia R2. En este caso, la suma de estas caídas de tensión individuales es igual a la tensión total de todo el circuito (tensión de alimentación Vin).
Vin = VR1 + VR2 – – – 1
La ecuación para la caída de voltaje individual en cada resistencia se puede calcular a partir de la ley de Ohm.
VR1 = I × R1 – – – 2
y VR2 = I × R2 – – – 3
Sin embargo, el voltaje a través de la resistencia R2 es VOUT.
Por lo tanto, VOUT = I × R2 – – – 4
Por lo tanto, de las ecuaciones 1, 2 y 3
Vin = I × R1 + I × R2 = I ×(R1 + R2)– – – 5
Sin embargo, el valor de la corriente I con respecto a la tensión de salida se puede escribir utilizando la Ecuación 4 como:
I = VOUT / R2 – – – 6
Usando la Ecuación 5 y la Ecuación 6
VOUT = Vin × (R¬2 / R1 + R2)
Por lo tanto, VOUT = VIN × R2/(R1+R2).
Para un circuito divisor de voltaje con múltiples salidas, el voltaje de salida se puede calcular como:

VX = V × (RX / REQ)
donde VX es el voltaje que se va a detectar.
RX es la resistencia total a través del voltaje de salida.
Los valores posibles para RX son los siguientes:
R1 entre P y P1
R1 + R2 entre P y P2
R1 + R2 + R3 entre P y P3
R1 + R2 + R3 + R4 entre P y P4.
RIko es la resistencia equivalente de la resistencia en la conexión en serie.
RIko = R1 + R2 + R3 + R4
V es el voltaje de la fuente de alimentación.
Por lo tanto, el voltaje de salida posible viene dado por:
V1 = V × R1 / RIko
V2 = V ×(R1 + R2) / RIko
V3 = V × (R1 + R2 + R3) / RIko
V4 = V × (R1 + R2 + R3 + R4) / RIko =V
Ejemplo de divisor de tensión
Considere el siguiente circuito divisor de voltaje.
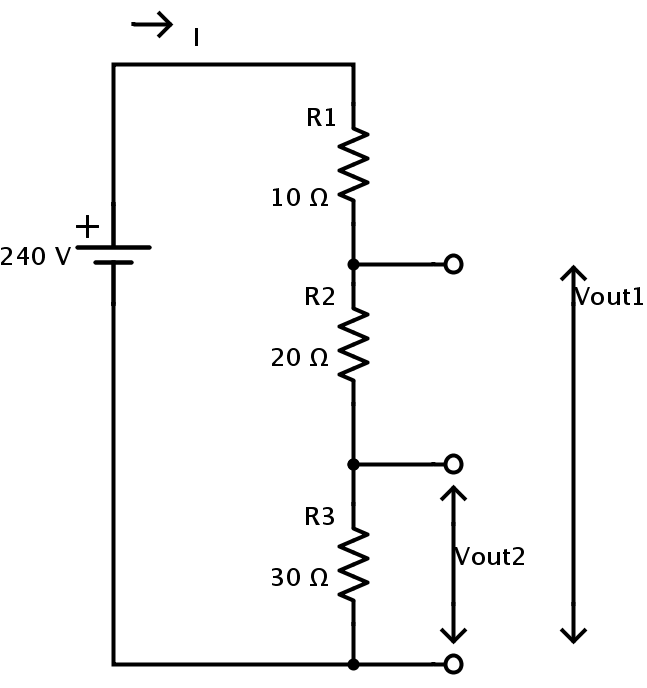
Consta de tres resistencias conectadas en serie para producir dos voltajes de salida. La tensión de alimentación es de 240 V.
Los valores de resistencia son R1 = 10 Ω, R2 = 20 Ω y R3 = 30 Ω.
Por lo tanto, la resistencia equivalente del circuito viene dada por:
RIko = R1 + R2 + R3 = 10 + 20 + 30 = 60 Ω。
Ahora los dos voltajes de salida posibles se pueden calcular de la siguiente manera
VSalida 1 = V × (R2 + R3) / REQ
VSalida 1 = 240 × (20 + 30) / 60
VSalida 1= 200 V.
VSalida 2 = V× R3 / REQ
VSalida 2= 240 × 30 / 60
VSalida 2 = 120 V.
La corriente en el circuito viene dada por:
I = V/RIko = 240 / 60 = 4 amperios.
Por lo tanto, la caída de voltaje individual para cada resistencia se puede calcular de la siguiente manera
VR1 = I × R1 = 4 × 10 = 40 V.
VR2 = I × R2 = 4 × 20 = 80 V.
VR3 = I × R3 = 4 ×30 = 120 V.
Aplicación del circuito divisor de voltaje
Cuando se resiste en serie, se forma un circuito divisor de voltaje. El principio del divisor de voltaje es la estructura de un potenciómetro que funciona como un regulador de voltaje simple.
Los circuitos divisores de voltaje se utilizan en circuitos de detección. Los sensores más utilizados en forma de circuitos divisores de tensión son los termistores y las resistencias dependientes de la luz.
Artículos Relacionados:
- Fórmula de potencia |Fórmulas de potencia para circuitos de CC y CA
- Amperios vs. Vatios vs. Voltios – ¿Cuál es la diferencia?
- ¿Cómo descargar un condensador? Usando un criador…
- La batería del coche es de CA o CC
- Diferencia entre circuitos abiertos y cerrados
- Cortadoras y abrazaderas de diodos