Capacitancia y carga

capacitancia

La capacitancia de un condensador se define como la capacidad del condensador para almacenar su carga máxima (Q) en el cuerpo. Aquí, la carga se almacena en forma de energía electrostática. La capacitancia se mide en unidades básicas del SI, es decir, faradios. Estas unidades pueden estar en microfaradios, nanofaradios, picofaradios o faradios. La ecuación para la capacitancia viene dada por:

C = Q/V = εA/d = ε0 εr A/d

En la fórmula anterior,

C es la capacitancia,

Q es la carga,

V es la diferencia de potencial entre las placas,

A es el área entre las placas,

d es la distancia entre las placas.

Constante dieléctrica ε dieléctrica

ε0 Constante dieléctrica en el espacio libre

Constante dieléctrica del espacio libre

Autocapacidad

Las características de autocapacitancia están relacionadas con los condensadores, especialmente con los conductores aislantes. Como su nombre indica, la capacitancia es una propiedad que aumenta la diferencia de potencial de un conductor aislado a 1 voltio. En general, los conductores ordinarios tienen capacitancia mutua. Esto también se mide en unidades SI, es decir, faradios.

La autocapacidad de una bombilla conductora con un radio “R” viene dada por:

C=4 πɛ_oR

A continuación se muestran los valores de autocapacitancia para algunos dispositivos estándar.

• Para la placa superior de un generador fan-des-graff con un radio de 20 cm, la autocapacitancia es de 22,24 pF.
• En el caso del planeta Tierra, la capacidad propia es de 710uF.

Capacitancia parásita

La capacitancia parásita es una capacitancia no deseada. Los condensadores introducen algo de capacitancia en el circuito. Sin embargo, componentes como resistencias, inductores e incluso cables tienen una cierta cantidad de capacitancia. Esto se denomina capacitancia parásita. En general, a altas frecuencias, se genera ruido en el circuito. Esta capacitancia indeseable es pequeña a menos que los conductores estén muy cerca unos de otros a largas distancias o áreas grandes.

La capacitancia parásita no se puede eliminar por completo, pero se puede reducir. Los diseñadores de circuitos deben prestar atención a la capacitancia parásita al diseñar circuitos. Se debe mantener la separación entre las piezas y las líneas para reducir la capacitancia innecesaria.

También se mide en unidades S.I, es decir, faradios.

Algunos ejemplos son la capacitancia entre las vueltas de una bobina, la capacitancia entre dos conductores adyacentes.

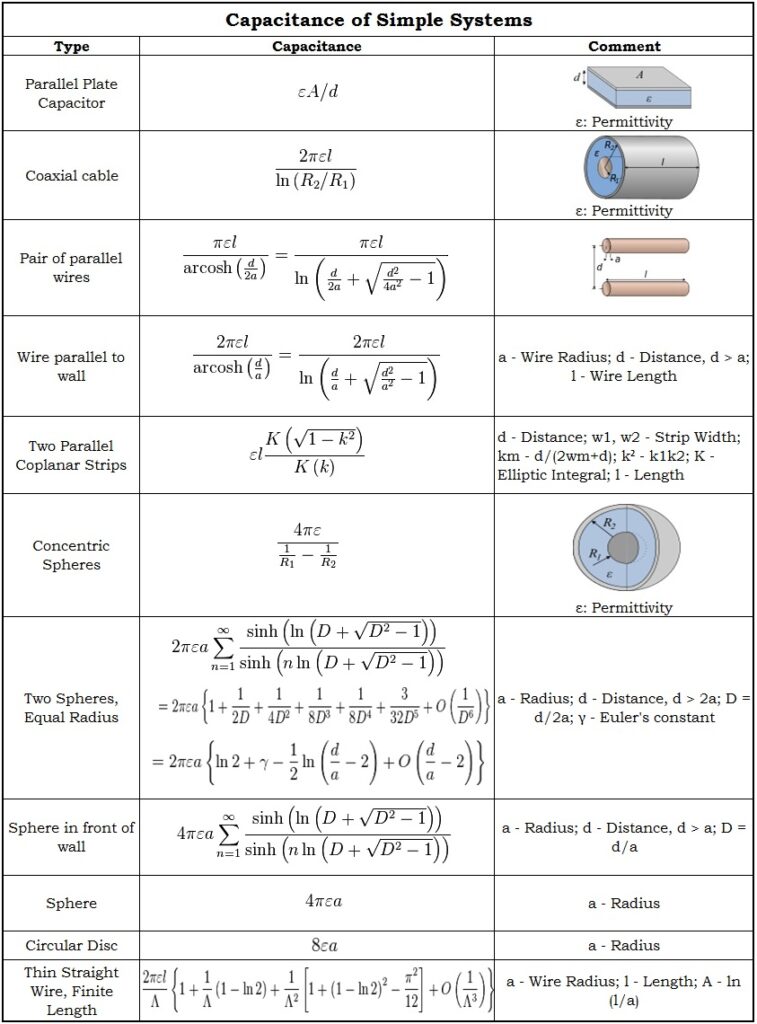
Capacitancia de un sistema simple

Calcular la capacitancia no es más que resolver el teorema de Laplace ∇ ²φ = 0 Hay un cierto potencial en la superficie del condensador. A continuación se presentan los valores de capacitancia y las fórmulas para algunos sistemas simples.

Carga de condensadores

La capacidad de un condensador para almacenar su carga máxima (Q) en una placa de metal se denomina valor de capacitancia (C). La polaridad de la carga acumulada puede ser negativa o positiva. Por ejemplo, poner una carga positiva (+ve) en una placa del condensador y una carga negativa (-ve) en otra. Las fórmulas de carga, capacitancia y voltaje se dan a continuación.

C = Q/V、Q = CV、V = Q/C

Por lo tanto, la carga de un condensador es directamente proporcional a su valor de capacitancia y a la diferencia de potencial entre las placas del condensador. La carga se mide en culombios.

1 Coulomb:

La carga de 1 culombio de un condensador se puede definir como la capacitancia de 1 faradio entre dos conductores que funcionan a un voltaje de 1 voltio.

Uso del aire como dieléctrico

La carga “Q” almacenada en un condensador con una capacitancia C, una diferencia de potencial “V” y aire como su dieléctrico viene dada por:

Q = C V = (ε× (A ×V)) /d

Usar sólidos como dieléctricos

La carga “Q” de un condensador dieléctrico sólido viene dada por la siguiente ecuación.

Q = C V = (ε0 ×εr× (A ×V)) /d

Aquí

ε0 es la constante dieléctrica del espacio libre,

εr es la constante dieléctrica relativa del material dieléctrico,

ε es la constante dieléctrica del dieléctrico.

De los dos casos anteriores, podemos ver lo siguiente

La carga del condensador es directamente proporcional al área de las placas, y la constante dieléctrica del dieléctrico entre las placas es inversamente proporcional a la distancia de separación entre las placas.

Por lo tanto, cuanto mayor sea el área de la placa, más carga y mayor será la distancia de separación entre las placas, menor carga tendrá el condensador.

Condensador de placa paralela

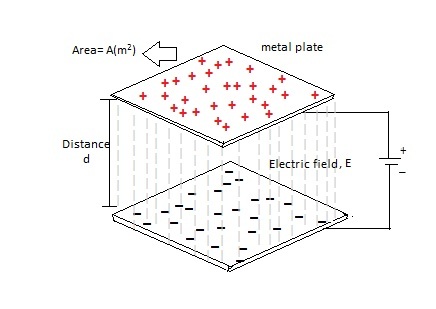
Figura 1: Circuito de condensador de placa plana

La figura anterior muestra un circuito de condensador de placa paralela. Como todos sabemos, la capacitancia es directamente proporcional al área de la placa (A) e inversamente proporcional a la distancia de separación (D) entre dos placas metálicas. El valor de capacitancia de un condensador de placa paralela viene dado por:

C = k ε0A/d

donde k es la constante dieléctrica y ε0 es la constante dieléctrica del espacio libre, que es igual a 8.854 X 10 -12 F / m. La constante dieléctrica (k) es un parámetro relacionado con los dieléctricos que aumentan su capacitancia en comparación con el aire. Cuanto mayor sea el área de superficie de la placa, mayor será el valor de capacitancia, y cuanto mayor sea la distancia de separación, mayor será el valor de capacitancia. Otro ejemplo de un circuito de condensador de placa paralela se muestra en la siguiente figura.

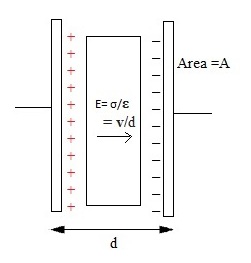
Figura 2: Condensador de placa paralela

Ejemplo de capacitancia n.º 1

A continuación, calcule la capacitancia de un condensador de placa paralela en un picofaradio con una superficie de placa de 200 cm2, separado a una distancia de 0,4 cm y separado con aire como dieléctrico.

La ecuación para la capacitancia de un condensador de placa paralela es la siguiente:

C = εA/d

donde ε = 8.854 X 10-12F/m

A = 200 cm2 = 0,02 m2

Profundidad = 0,4 cm = 0,004 m

A continuación, sustituya estos valores por la fórmula anterior.

C = 8,854 X 10-12 * (0,02 m2/0,004 m) = 44,27 pF

Aquí, la capacitancia del condensador de placa paralela es de 44,27 pF

Carga y descarga de condensadores

El siguiente circuito se utiliza para ilustrar las características de carga-descarga de los condensadores. Suponga que el condensador indicado en el circuito está completamente descargado. En este circuito, el valor del condensador es de 100 uF y el voltaje de alimentación aplicado al circuito es de 12 V.

Ahora el interruptor conectado al condensador en el circuito se mueve al punto A. Luego, el condensador comienza a cargarse con la corriente de carga (i), y este condensador también está completamente cargado. El voltaje de carga a través del condensador es igual al voltaje de alimentación cuando el condensador está completamente cargado, es decir, VS = VC = 12V. Cuando el condensador está completamente cargado, significa que el condensador mantiene una carga de voltaje constante incluso cuando el voltaje de alimentación está desconectado del circuito.

En el caso de un condensador ideal, la carga del condensador se mantiene constante, pero en el caso de un condensador típico, un condensador completamente cargado se descarga lentamente debido a la corriente de fuga.

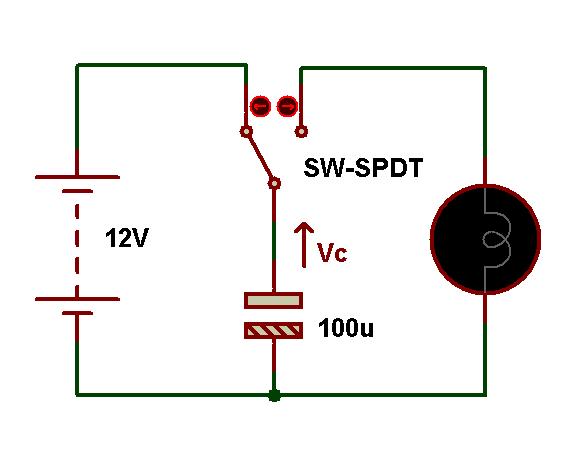
Figura: Circuito del condensador de carga/descarga

Cuando el interruptor se mueve a la posición B, el condensador se descarga lentamente encendiendo la lámpara conectada al circuito. Finalmente, se descarga a cero por completo. Cuando el condensador está completamente cargado, la lámpara inicialmente brillará intensamente, pero a medida que disminuye la carga del condensador, el brillo de la lámpara disminuye.

Ejemplo de carga de condensador n.º 2

Ahora, calculemos la carga del condensador en el circuito anterior, la fórmula para la carga del condensador es

Q = CV

donde C = 100uF

V = 12V

A continuación, sustituya estos valores por la fórmula anterior.

Q = 100uF * 12V = 1.2mC

Por lo tanto, la carga del condensador en el circuito anterior es de 1,2 mC.

Corriente que fluye a través del condensador

La corriente (i) que fluye a través de un circuito eléctrico es la velocidad de carga (Q) que fluye con respecto al tiempo. Sin embargo, la carga del condensador es directamente proporcional al voltaje que se le aplica. La relación entre la carga, la corriente y el voltaje de un condensador viene dada por la siguiente ecuación:

I

Sabemos que

Q = CV

V = Q/C

V

Q

La relación entre corriente y voltaje viene dada por I

A partir de esta relación, podemos determinar que la corriente que fluye a través de un condensador en un circuito es la tasa de cambio entre la capacitancia y el voltaje aplicado al circuito.Es el producto de. La corriente que fluye a través de un condensador es directamente proporcional a la capacitancia y la tasa de voltaje del condensador.

Cuanto mayor sea la corriente, mayor será la capacitancia del circuito, y cuanto mayor sea el voltaje aplicado, mayor será la corriente que fluye a través del circuito. Si el voltaje es constante, la carga también es constante. Por lo tanto, no hay flujo de carga. Por lo tanto, la corriente que fluye a través del circuito será cero.

Unidades de capacitancia (faradios)

Josiah Latimer Clark en 1861 fue el primero en utilizar el término Farad. El faradio es la unidad estándar de capacitancia. Es una unidad extremadamente grande para su capacitancia.

La capacitancia de 1 faradio se define como la capacitancia con una carga de 1 culombio que funciona a un voltaje de 1 voltio.

C = Q/V

1 faradio = 1 coleón / 1 voltio

Actualmente, los condensadores están disponibles en grandes valores de capacitancia de varios cientos de faradios. Estos condensadores con altos valores de capacitancia se denominan “supercondensadores”. Debido a sus altos valores de capacitancia, estos condensadores utilizan una gran superficie para proporcionar alta energía.

A bajos voltajes, los supercondensadores tienen la capacidad de almacenar alta energía a altos valores de capacitancia. Estos supercondensadores de alta energía se utilizan en dispositivos portátiles de mano para reemplazar condensadores de litio grandes, pesados y costosos porque almacenan alta energía como las baterías. Estos condensadores también se utilizan en los sistemas de audio y video de los vehículos mediante la sustitución de baterías altas.

Subunidad de Farad

La unidad estándar de capacitancia es el faradio. Sin embargo, generalmente se trata de una unidad grande para medir la capacitancia. Este faradio tiene varias subunidades. Son microfaradios (uF), nanofaradios (nF) y picofaradios (pF).

La relación entre todas estas subunidades con faradios es la siguiente

1 microfaradio (uF) = (1/1000000) F = 10-6 F

1 nanofaradio (uF) = (1/10000000000) F = 10-9 F

1 picofaradio (uF) = (1/100000000000000) F = 10-12 F

A continuación, veremos algunas conversiones entre subunidades de capacitancia.

(i) Conversión de 33 pF a nF = > 33 pF = 0,033 nF

ii) Conversión de 22 nF a uF = > 22 nF = 0,022 uF

(iii) Conversión de 11uF a F = > 11uF = 0.11F

Energía del condensador

La energía es la cantidad de trabajo en el campo electrostático para cargar completamente el condensador. En los condensadores en las primeras etapas de carga, la carga Q se mueve de una placa a otra entre placas. Esta carga se intercambia entre las dos placas del condensador, ya sea +Q o -Q. Después de la conversión de la carga, se forma un campo eléctrico entre las placas, en cuyo caso se requiere trabajo adicional para cargar completamente el condensador. Este trabajo adicional se denomina energía almacenada en el condensador. La energía se mide en unidades de julios (J). Ahora estamos viendo esta ecuación de energía y trabajo.

dW = V dQ

dW = (Q/C) dQ

Después de la integración de la ecuación anterior,

W = Q²/2C

W = (CV)²/2C

W = CV²/2 julios

Por último, la energía almacenada en el condensador es:

Energía (W) = CV²/2 julios

A continuación, se calcula la energía almacenada en un condensador con una capacitancia de 200 μF que funciona a una tensión de 12 V.

W = CV²/2

W = (200×10)^-6×12²)/2 = 14,4 m J

Artículos relacionados en la web

• Preguntas frustrantes sobre la energía del condensador