Análisis de Big Data – Guía rápida

El volumen de datos que uno tiene que manejar se ha disparado a niveles inimaginables en la última década y, al mismo tiempo, el precio del almacenamiento de datos se ha reducido sistemáticamente. Las empresas privadas y las instituciones de investigación capturan terabytes de datos sobre las interacciones de sus usuarios, negocios, redes sociales y también sensores de dispositivos como teléfonos móviles y automóviles. El desafío de esta era es dar sentido a este mar de datos. Aquí es donde entra en escena el análisis de big data .

Big Data Analytics implica en gran medida recopilar datos de diferentes fuentes, manipularlos de manera que estén disponibles para ser consumidos por los analistas y, finalmente, entregar productos de datos útiles para el negocio de la organización.

El proceso de convertir grandes cantidades de datos en bruto no estructurados, recuperados de diferentes fuentes en un producto de datos útil para las organizaciones, constituye el núcleo de Big Data Analytics.

Big Data Analytics – Ciclo de vida de los datos

Ciclo de vida de la minería de datos tradicional

Con el fin de proporcionar un marco para organizar el trabajo que necesita una organización y brindar información clara de Big Data, es útil pensar en ello como un ciclo con diferentes etapas. No es de ninguna manera lineal, lo que significa que todas las etapas están relacionadas entre sí. Este ciclo tiene similitudes superficiales con el ciclo de minería de datos más tradicional como se describe en la metodología CRISP .

Metodología CRISP-DM

La metodología CRISP-DM , que significa Cross Industry Standard Process for Data Mining, es un ciclo que describe los enfoques comúnmente utilizados por los expertos en minería de datos para abordar problemas en la minería de datos de BI tradicional. Todavía se usa en equipos de minería de datos de BI tradicionales.

Echa un vistazo a la siguiente ilustración. Muestra las principales etapas del ciclo según lo descrito por la metodología CRISP-DM y cómo están interrelacionadas.

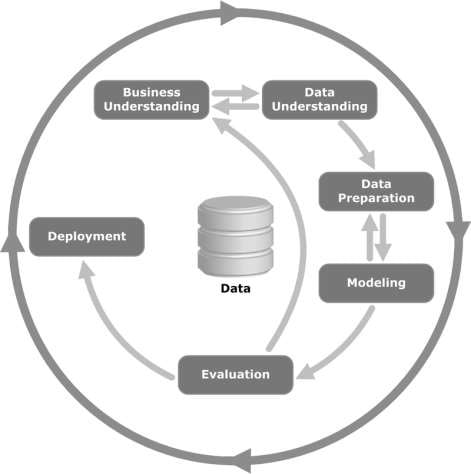
CRISP-DM se concibió en 1996 y al año siguiente se puso en marcha como un proyecto de la Unión Europea bajo la iniciativa de financiación ESPRIT. El proyecto fue liderado por cinco empresas: SPSS, Teradata, Daimler AG, NCR Corporation y OHRA (una compañía de seguros). El proyecto finalmente se incorporó a SPSS. La metodología es extremadamente detallada y orientada a cómo se debe especificar un proyecto de minería de datos.

Ahora aprendamos un poco más sobre cada una de las etapas involucradas en el ciclo de vida de CRISP-DM:

• Entendimiento del negocio : esta fase inicial se enfoca en comprender los objetivos y requisitos del proyecto desde una perspectiva comercial, y luego convertir este conocimiento en una definición del problema de minería de datos. Se diseña un plan preliminar para alcanzar los objetivos. Se puede usar un modelo de decisión, especialmente uno construido usando el modelo de decisión y el estándar de notación.
• Comprensión de datos : la fase de comprensión de datos comienza con una recopilación de datos inicial y continúa con actividades para familiarizarse con los datos, identificar problemas de calidad de datos, descubrir las primeras ideas sobre los datos o detectar subconjuntos interesantes para formar hipótesis para ocultos. información.
• Preparación de datos : la fase de preparación de datos cubre todas las actividades para construir el conjunto de datos final (datos que se incorporarán a la(s) herramienta(s) de modelado) a partir de los datos sin procesar iniciales. Es probable que las tareas de preparación de datos se realicen varias veces y no en un orden prescrito. Las tareas incluyen la selección de tablas, registros y atributos, así como la transformación y limpieza de datos para herramientas de modelado.
• Modelado : en esta fase, se seleccionan y aplican varias técnicas de modelado y sus parámetros se calibran a valores óptimos. Por lo general, existen varias técnicas para el mismo tipo de problema de minería de datos. Algunas técnicas tienen requisitos específicos sobre la forma de los datos. Por lo tanto, a menudo se requiere volver a la fase de preparación de datos.
• Evaluación : en esta etapa del proyecto, ha creado un modelo (o modelos) que parecen tener alta calidad, desde la perspectiva del análisis de datos. Antes de proceder a la implementación final del modelo, es importante evaluar el modelo a fondo y revisar los pasos ejecutados para construir el modelo, para asegurarse de que logre correctamente los objetivos comerciales.

Un objetivo clave es determinar si existe algún tema comercial importante que no se haya considerado lo suficiente. Al final de esta fase, se debe llegar a una decisión sobre el uso de los resultados de la minería de datos.

• Implementación : la creación del modelo generalmente no es el final del proyecto. Incluso si el propósito del modelo es aumentar el conocimiento de los datos, el conocimiento obtenido deberá organizarse y presentarse de una manera que sea útil para el cliente.

Según los requisitos, la fase de implementación puede ser tan simple como generar un informe o tan compleja como implementar una puntuación de datos repetible (por ejemplo, asignación de segmentos) o un proceso de extracción de datos.

En muchos casos, será el cliente, no el analista de datos, quien llevará a cabo los pasos de implementación. Incluso si el analista implementa el modelo, es importante que el cliente comprenda por adelantado las acciones que deberán llevarse a cabo para hacer uso de los modelos creados.

Metodología SEMMA

SEMMA es otra metodología desarrollada por SAS para el modelado de minería de datos. Son las siglas de S ample, E xplore, M odify, M odel y A sses. He aquí una breve descripción de sus etapas:

• Muestra : el proceso comienza con el muestreo de datos, por ejemplo, seleccionando el conjunto de datos para modelar. El conjunto de datos debe ser lo suficientemente grande para contener suficiente información para recuperar, pero lo suficientemente pequeño para ser utilizado de manera eficiente. Esta fase también se ocupa de la partición de datos.
• Explorar : esta fase cubre la comprensión de los datos al descubrir relaciones anticipadas e imprevistas entre las variables, y también anomalías, con la ayuda de la visualización de datos.
• Modificar : la fase Modificar contiene métodos para seleccionar, crear y transformar variables en preparación para el modelado de datos.
• Modelo : en la fase Modelo, la atención se centra en la aplicación de varias técnicas de modelado (minería de datos) en las variables preparadas para crear modelos que posiblemente proporcionen el resultado deseado.
• Evaluar : la evaluación de los resultados del modelado muestra la confiabilidad y utilidad de los modelos creados.

La principal diferencia entre CRISM–DM y SEMMA es que SEMMA se enfoca en el aspecto de modelado, mientras que CRISP-DM le da más importancia a las etapas del ciclo antes del modelado, como comprender el problema comercial a resolver, comprender y preprocesar los datos a ser utilizado como entrada, por ejemplo, algoritmos de aprendizaje automático.

Ciclo de vida de grandes datos

En el contexto de big data actual, los enfoques anteriores son incompletos o subóptimos. Por ejemplo, la metodología SEMMA ignora por completo la recopilación y el preprocesamiento de datos de diferentes fuentes de datos. Estas etapas normalmente constituyen la mayor parte del trabajo en un proyecto exitoso de big data.

Un ciclo de análisis de big data puede describirse mediante la siguiente etapa:

• Definición de problema empresarial
• Investigación
• Evaluación de Recursos Humanos
• Adquisición de datos
• Transporte de datos
• Almacenamiento de datos
• Análisis exploratorio de datos
• Preparación de datos para modelado y evaluación
• Modelado
• Implementación

En esta sección, arrojaremos algo de luz sobre cada una de estas etapas del ciclo de vida de big data.

Definición de problema empresarial

Este es un punto común en el ciclo de vida tradicional de BI y análisis de big data. Normalmente es una etapa no trivial de un proyecto de big data para definir el problema y evaluar correctamente cuánto beneficio potencial puede tener para una organización. Parece obvio mencionar esto, pero hay que evaluar cuáles son las ganancias y costos esperados del proyecto.

Investigación

Analiza qué han hecho otras empresas en la misma situación. Esto implica buscar soluciones que sean razonables para su empresa, aunque implique adaptar otras soluciones a los recursos y requerimientos que tiene su empresa. En esta etapa se debe definir una metodología para las etapas futuras.

Evaluación de Recursos Humanos

Una vez definido el problema, es razonable continuar analizando si el personal actual es capaz de completar el proyecto con éxito. Es posible que los equipos de BI tradicionales no sean capaces de ofrecer una solución óptima en todas las etapas, por lo que se debe considerar antes de iniciar el proyecto si es necesario subcontratar una parte del proyecto o contratar a más personas.

Adquisición de datos

Esta sección es clave en un ciclo de vida de big data; define qué tipo de perfiles serían necesarios para entregar el producto de datos resultante. La recopilación de datos es un paso no trivial del proceso; normalmente implica recopilar datos no estructurados de diferentes fuentes. Para dar un ejemplo, podría implicar escribir un rastreador para recuperar reseñas de un sitio web. Esto implica tratar con texto, tal vez en diferentes idiomas, lo que normalmente requiere una cantidad significativa de tiempo para completarse.

Transporte de datos

Una vez que los datos se recuperan, por ejemplo, de la web, deben almacenarse en un formato fácil de usar. Para continuar con los ejemplos de revisiones, supongamos que los datos se recuperan de diferentes sitios donde cada uno tiene una visualización diferente de los datos.

Supongamos que una fuente de datos brinda reseñas en términos de calificación en estrellas, por lo tanto, es posible leer esto como un mapeo para la variable de respuesta y ∈ {1, 2, 3, 4, 5} . Otra fuente de datos brinda reseñas utilizando un sistema de dos flechas, una para votar a favor y la otra para votar a favor. Esto implicaría una variable de respuesta de la forma y ∈ {positiva, negativa} .

Para combinar ambas fuentes de datos, se debe tomar una decisión para que estas dos representaciones de respuesta sean equivalentes. Esto puede implicar convertir la representación de respuesta de la primera fuente de datos a la segunda forma, considerando una estrella como negativa y cinco estrellas como positivas. Este proceso a menudo requiere una gran asignación de tiempo para ser entregado con buena calidad.

Almacenamiento de datos

Una vez que se procesan los datos, a veces es necesario almacenarlos en una base de datos. Las tecnologías de big data ofrecen multitud de alternativas en este punto. La alternativa más común es utilizar el sistema de archivos Hadoop para el almacenamiento que proporciona a los usuarios una versión limitada de SQL, conocida como lenguaje de consulta HIVE. Esto permite que la mayoría de las tareas de análisis se realicen de manera similar a como se haría en los almacenes de datos de BI tradicionales, desde la perspectiva del usuario. Otras opciones de almacenamiento a considerar son MongoDB, Redis y SPARK.

Esta etapa del ciclo está relacionada con el conocimiento de los recursos humanos en cuanto a sus habilidades para implementar diferentes arquitecturas. Las versiones modificadas de los almacenes de datos tradicionales todavía se utilizan en aplicaciones a gran escala. Por ejemplo, teradata e IBM ofrecen bases de datos SQL que pueden manejar terabytes de datos; Las soluciones de código abierto como PostgreSQL y MySQL todavía se utilizan para aplicaciones a gran escala.

Aunque existen diferencias en el funcionamiento de los distintos almacenamientos en segundo plano, desde el lado del cliente, la mayoría de las soluciones proporcionan una API de SQL. Por lo tanto, tener una buena comprensión de SQL sigue siendo una habilidad clave para el análisis de big data.

Esta etapa a priori parece ser el tema más importante, en la práctica esto no es cierto. Ni siquiera es una etapa imprescindible. Es posible implementar una solución de big data que estaría trabajando con datos en tiempo real, por lo que en este caso, solo necesitamos recopilar datos para desarrollar el modelo y luego implementarlo en tiempo real. Por lo tanto, no sería necesario almacenar formalmente los datos en absoluto.

Análisis exploratorio de datos

Una vez que los datos se han limpiado y almacenado de manera que se puedan recuperar conocimientos, la fase de exploración de datos es obligatoria. El objetivo de esta etapa es entender los datos, esto normalmente se hace con técnicas estadísticas y también graficando los datos. Esta es una buena etapa para evaluar si la definición del problema tiene sentido o es factible.

Preparación de datos para modelado y evaluación

Esta etapa implica remodelar los datos limpios recuperados previamente y utilizar el preprocesamiento estadístico para la imputación de valores faltantes, la detección de valores atípicos, la normalización, la extracción de características y la selección de características.

Modelado

La etapa anterior debería haber producido varios conjuntos de datos para entrenamiento y prueba, por ejemplo, un modelo predictivo. Esta etapa implica probar diferentes modelos y esperar resolver el problema comercial en cuestión. En la práctica, normalmente se desea que el modelo proporcione una idea del negocio. Finalmente, se selecciona el mejor modelo o combinación de modelos evaluando su desempeño en un conjunto de datos omitido.

Implementación

En esta etapa, el producto de datos desarrollado se implementa en el pipeline de datos de la empresa. Esto implica configurar un esquema de validación mientras el producto de datos está funcionando, con el fin de realizar un seguimiento de su rendimiento. Por ejemplo, en el caso de implementar un modelo predictivo, esta etapa implicaría aplicar el modelo a nuevos datos y una vez que la respuesta esté disponible, evaluar el modelo.

Análisis de Big Data – Metodología

En términos de metodología, el análisis de big data difiere significativamente del enfoque estadístico tradicional del diseño experimental. El análisis comienza con los datos. Normalmente modelamos los datos de una manera para explicar una respuesta. Los objetivos de este enfoque son predecir el comportamiento de la respuesta o comprender cómo las variables de entrada se relacionan con una respuesta. Normalmente, en los diseños experimentales estadísticos, se desarrolla un experimento y, como resultado, se recuperan los datos. Esto permite generar datos de una manera que puede ser utilizada por un modelo estadístico, donde ciertos supuestos son válidos, como la independencia, la normalidad y la aleatorización.

En el análisis de big data, se nos presentan los datos. No podemos diseñar un experimento que cumpla con nuestro modelo estadístico favorito. En aplicaciones de análisis a gran escala, se necesita una gran cantidad de trabajo (normalmente el 80 % del esfuerzo) solo para limpiar los datos, de modo que pueda ser utilizado por un modelo de aprendizaje automático.

No tenemos una metodología única a seguir en aplicaciones reales a gran escala. Normalmente una vez definido el problema de negocio se necesita una etapa de investigación para diseñar la metodología a utilizar. Sin embargo, las pautas generales son relevantes para ser mencionadas y se aplican a casi todos los problemas.

Una de las tareas más importantes en el análisis de big data es el modelado estadístico , es decir, problemas de clasificación o regresión supervisados ​​y no supervisados. Una vez que los datos se limpian y preprocesan, disponibles para el modelado, se debe tener cuidado al evaluar diferentes modelos con métricas de pérdida razonables y luego, una vez que se implementa el modelo, se debe informar una evaluación adicional y los resultados. Un error común en el modelado predictivo es simplemente implementar el modelo y nunca medir su desempeño.

Big Data Analytics – Entregables principales

Como se mencionó en el ciclo de vida de big data, los productos de datos que resultan del desarrollo de un producto de big data son, en la mayoría de los casos, algunos de los siguientes:

• Implementación de aprendizaje automático : podría ser un algoritmo de clasificación, un modelo de regresión o un modelo de segmentación.
• Sistema de recomendación : el objetivo es desarrollar un sistema que recomiende opciones según el comportamiento del usuario. Netflix es el ejemplo característico de este producto de datos, donde en base a las valoraciones de los usuarios, se recomiendan otras películas.
• Tablero : normalmente, las empresas necesitan herramientas para visualizar datos agregados. Un tablero es un mecanismo gráfico para hacer que estos datos sean accesibles.
• Análisis Ad-Hoc − Normalmente las áreas de negocio tienen preguntas, hipótesis o mitos que pueden ser respondidos haciendo análisis ad-hoc con datos.

Análisis de Big Data: partes interesadas clave

En las grandes organizaciones, para desarrollar con éxito un proyecto de big data, es necesario contar con una gestión que respalde el proyecto. Esto normalmente implica encontrar una manera de mostrar las ventajas comerciales del proyecto. No tenemos una solución única para el problema de encontrar patrocinadores para un proyecto, pero a continuación se dan algunas pautas:

• Consulta quiénes y dónde están los patrocinadores de otros proyectos similares al que te interesa.
• Tener contactos personales en puestos gerenciales clave ayuda, por lo que cualquier contacto puede activarse si el proyecto es prometedor.
• ¿Quién se beneficiaría de su proyecto? ¿Quién sería su cliente una vez que el proyecto esté en marcha?
• Desarrolle una propuesta simple, clara y emocionante y compártala con los actores clave de su organización.

La mejor manera de encontrar patrocinadores para un proyecto es comprender el problema y cuál sería el producto de datos resultante una vez que se haya implementado. Esta comprensión dará una ventaja para convencer a la gerencia de la importancia del proyecto de big data.

Análisis de Big Data – Analista de datos

Un analista de datos tiene un perfil orientado a la generación de informes, con experiencia en la extracción y el análisis de datos de los almacenes de datos tradicionales utilizando SQL. Sus tareas normalmente se encuentran en el lado del almacenamiento de datos o en la presentación de informes de resultados comerciales generales. El almacenamiento de datos no es simple, simplemente es diferente a lo que hace un científico de datos.

Muchas organizaciones tienen dificultades para encontrar científicos de datos competentes en el mercado. Sin embargo, es una buena idea seleccionar posibles analistas de datos y enseñarles las habilidades relevantes para convertirse en científicos de datos. Esta no es una tarea trivial y normalmente involucraría a la persona que realiza una maestría en un campo cuantitativo, pero definitivamente es una opción viable. Las habilidades básicas que debe tener un analista de datos competente se enumeran a continuación:

• Comprensión empresarial
• programación SQL
• Diseño e implementación de informes
• Desarrollo de cuadros de mando

Análisis de Big Data – Científico de datos

El papel de un científico de datos normalmente se asocia con tareas como el modelado predictivo, el desarrollo de algoritmos de segmentación, sistemas de recomendación, marcos de pruebas A/B y, a menudo, trabajar con datos sin estructurar sin procesar.

La naturaleza de su trabajo exige un profundo conocimiento de las matemáticas, la estadística aplicada y la programación. Hay algunas habilidades comunes entre un analista de datos y un científico de datos, por ejemplo, la capacidad de consultar bases de datos. Ambos analizan datos, pero la decisión de un científico de datos puede tener un mayor impacto en una organización.

Aquí hay un conjunto de habilidades que un científico de datos normalmente necesita tener:

• Programación en un paquete estadístico como: R, Python, SAS, SPSS o Julia
• Capaz de limpiar, extraer y explorar datos de diferentes fuentes
• Investigación, diseño e implementación de modelos estadísticos
• Profundos conocimientos estadísticos, matemáticos e informáticos.

En el análisis de big data, las personas normalmente confunden el rol de un científico de datos con el de un arquitecto de datos. En realidad, la diferencia es bastante simple. Un arquitecto de datos define las herramientas y la arquitectura en la que se almacenarían los datos, mientras que un científico de datos utiliza esta arquitectura. Por supuesto, un científico de datos debe poder configurar nuevas herramientas si es necesario para proyectos ad-hoc, pero la definición y el diseño de la infraestructura no deben ser parte de su tarea.

Big Data Analytics – Definición del problema

A través de este tutorial, desarrollaremos un proyecto. Cada capítulo subsiguiente de este tutorial se ocupa de una parte del proyecto más grande en la sección de miniproyecto. Se cree que esta es una sección de tutorial aplicada que brindará exposición a un problema del mundo real. En este caso, comenzaríamos con la definición del problema del proyecto.

Descripción del Proyecto

El objetivo de este proyecto sería desarrollar un modelo de aprendizaje automático para predecir el salario por hora de las personas utilizando el texto de su currículum vitae (CV) como entrada.

Usando el marco definido anteriormente, es simple definir el problema. Podemos definir X = {x ₁ , x ₂ , …, x _n } como los CV’s de los usuarios, donde cada característica puede ser, de la forma más sencilla posible, la cantidad de veces que aparece esta palabra. Entonces la respuesta es valor real, estamos tratando de predecir el salario por hora de los individuos en dólares.

Estas dos consideraciones son suficientes para concluir que el problema presentado puede resolverse con un algoritmo de regresión supervisada.

Definición del problema

La definición del problema es probablemente una de las etapas más complejas y más descuidadas en la tubería de análisis de big data. Para definir el problema que resolvería un producto de datos, la experiencia es obligatoria. La mayoría de los aspirantes a científicos de datos tienen poca o ninguna experiencia en esta etapa.

La mayoría de los problemas de big data se pueden categorizar de las siguientes maneras:

• Clasificación supervisada
• regresión supervisada
• Aprendizaje sin supervisión
• Aprendiendo a clasificar

Ahora aprendamos más sobre estos cuatro conceptos.

Clasificación Supervisada

Dada una matriz de características X = {x ₁ , x ₂ , …, x _n } desarrollamos un modelo M para predecir diferentes clases definidas como y = {c ₁ , c ₂ , …, c _n } . Por ejemplo: dados los datos transaccionales de los clientes en una compañía de seguros, es posible desarrollar un modelo que prediga si un cliente abandonaría o no. Este último es un problema de clasificación binaria, donde hay dos clases o variables objetivo: churn y no churn.

Otros problemas involucran predecir más de una clase, nos podría interesar hacer reconocimiento de dígitos, por lo tanto el vector de respuesta quedaría definido como: y = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} , un modelo de última generación sería una red neuronal convolucional y la matriz de características se definiría como los píxeles de la imagen.

Regresión supervisada

En este caso, la definición del problema es bastante similar al ejemplo anterior; la diferencia depende de la respuesta. En un problema de regresión, la respuesta y ∈ ℜ, esto significa que la respuesta tiene un valor real. Por ejemplo, podemos desarrollar un modelo para predecir el salario por hora de las personas dado el corpus de su CV.

Aprendizaje sin supervisión

La gerencia a menudo está sedienta de nuevos conocimientos. Los modelos de segmentación pueden proporcionar esta información para que el departamento de marketing desarrolle productos para diferentes segmentos. Un buen enfoque para desarrollar un modelo de segmentación, en lugar de pensar en algoritmos, es seleccionar características que sean relevantes para la segmentación que se desea.

Por ejemplo, en una empresa de telecomunicaciones, es interesante segmentar a los clientes por el uso que hacen del celular. Esto implicaría descartar características que no tienen nada que ver con el objetivo de segmentación e incluir solo aquellas que sí lo tienen. En este caso, esto sería seleccionar características como la cantidad de SMS utilizados en un mes, la cantidad de minutos entrantes y salientes, etc.

Aprendiendo a clasificar

Este problema puede considerarse como un problema de regresión, pero tiene características particulares y merece un tratamiento aparte. El problema consiste en dar una colección de documentos que buscamos para encontrar la ordenación más relevante dada una consulta. Para desarrollar un algoritmo de aprendizaje supervisado, es necesario etiquetar qué tan relevante es un orden, dada una consulta.

Es relevante notar que para desarrollar un algoritmo de aprendizaje supervisado, es necesario etiquetar los datos de entrenamiento. Esto significa que para entrenar un modelo que, por ejemplo, reconozca dígitos de una imagen, necesitamos etiquetar una cantidad significativa de ejemplos a mano. Hay servicios web que pueden acelerar este proceso y se usan comúnmente para esta tarea, como Amazon Mechanical Turk. Está comprobado que los algoritmos de aprendizaje mejoran su rendimiento cuando se les proporciona más datos, por lo que etiquetar una buena cantidad de ejemplos es prácticamente obligatorio en el aprendizaje supervisado.

Big Data Analytics – Recopilación de datos

La recopilación de datos juega el papel más importante en el ciclo de Big Data. Internet proporciona fuentes de datos casi ilimitadas para una variedad de temas. La importancia de esta área depende del tipo de negocio, pero las industrias tradicionales pueden adquirir una fuente diversa de datos externos y combinarlos con sus datos transaccionales.

Por ejemplo, supongamos que nos gustaría construir un sistema que recomiende restaurantes. El primer paso sería recopilar datos, en este caso, reseñas de restaurantes de diferentes sitios web y almacenarlos en una base de datos. Como estamos interesados ​​en texto sin procesar y lo usaríamos para análisis, no es tan relevante dónde se almacenarían los datos para desarrollar el modelo. Esto puede sonar contradictorio con las principales tecnologías de big data, pero para implementar una aplicación de big data, simplemente necesitamos hacer que funcione en tiempo real.

Mini proyecto de Twitter

Una vez definido el problema, la siguiente etapa es recolectar los datos. La siguiente idea de miniproyecto es trabajar en la recopilación de datos de la web y estructurarlos para usarlos en un modelo de aprendizaje automático. Recopilaremos algunos tweets de la API de descanso de Twitter utilizando el lenguaje de programación R.

En primer lugar, cree una cuenta de Twitter y luego siga las instrucciones en la viñeta del paquete de Twitter para crear una cuenta de desarrollador de Twitter. Este es un resumen de esas instrucciones:

• Vaya a https://twitter.com/apps/new e inicie sesión.
• Después de completar la información básica, vaya a la pestaña “Configuración” y seleccione “Leer, escribir y acceder a mensajes directos”.
• Asegúrese de hacer clic en el botón Guardar después de hacer esto
• En la pestaña “Detalles”, tome nota de su clave de consumidor y secreto de consumidor
• En su sesión de R, usará la clave de API y los valores secretos de API
• Finalmente ejecute el siguiente script. Esto instalará el paquete twitteR desde su repositorio en github.

install.packages(c("devtools", "rjson", "bit64", "httr"))

# Make sure to restart your R session at this point

library(devtools)

install_github("geoffjen

Nos interesa obtener datos donde se incluya la cadena “big mac” y averiguar qué temas destacan al respecto. Para hacer esto, el primer paso es recopilar los datos de Twitter. A continuación se muestra nuestro script R para recopilar los datos necesarios de Twitter. Este código también está disponible en el archivo bda/part1/collect_data/collect_data_twitter.R.

rm(list = ls(all = TRUE)); gc() # Clears the global environment

library(twitteR)

Sys.setlocale(category = "LC_ALL", locale = "C")

### Replace the xxx’s with the values you got from the previous instructions

# consumer_key = "xxxxxxxxxxxxxxxxxxxx"

# consumer_secret = "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"

# access_token = "xxxxxxxxxx-xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"

# access_token_secret= "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"

# Connect to twitter rest API

setup_twitter_oauth(consumer_key, consumer_secret, access_token, access_token_secret)

# Get tweets related to big mac

tweets <- searchTwitter(’big mac’, n = 200, lang = ’en’)

df <- twListToDF(tweets)

# Take a look at the data

head(df)

# Check which device is most used

sources <- sapply(tweets, function(x) x$getStatusSource())

sources <- gsub("</a>", "", sources)

sources <- strsplit(sources, ">")

sources <- sapply(sources, function(x) ifelse(length(x) > 1, x[2], x[1]))

source_table = table(sources)

source_table = source_table[source_table > 1]

freq = source_table[order(source_table, decreasing = T)]

as.data.frame(freq)

# Frequency

# Twitter for iPhone 71

# Twitter for Android 29

# Twitter Web Client 25

# recognia 20

Big Data Analytics – Limpieza de datos

Una vez recopilados los datos, normalmente disponemos de diversas fuentes de datos con diferentes características. El paso más inmediato sería homogeneizar estas fuentes de datos y seguir desarrollando nuestro producto de datos. Sin embargo, depende del tipo de datos. Deberíamos preguntarnos si es práctico homogeneizar los datos.

Tal vez las fuentes de datos sean completamente diferentes y la pérdida de información sea grande si se homogeneizan las fuentes. En este caso, podemos pensar en alternativas. ¿Puede una fuente de datos ayudarme a construir un modelo de regresión y la otra un modelo de clasificación? ¿Es posible trabajar con la heterogeneidad a nuestro favor en lugar de simplemente perder información? Tomar estas decisiones es lo que hace que el análisis sea interesante y desafiante.

En el caso de las reseñas, es posible tener un idioma para cada fuente de datos. Una vez más, tenemos dos opciones:

• Homogeneización − Se trata de traducir diferentes idiomas al idioma donde tenemos más datos. La calidad de los servicios de traducción es aceptable, pero si quisiéramos traducir cantidades masivas de datos con una API, el costo sería significativo. Hay herramientas de software disponibles para esta tarea, pero eso también sería costoso.
• Heterogenización − ¿Sería posible desarrollar una solución para cada idioma? Como es sencillo detectar el idioma de un corpus, podríamos desarrollar un recomendador para cada idioma. Esto implicaría más trabajo en términos de ajustar cada recomendador de acuerdo con la cantidad de idiomas disponibles, pero definitivamente es una opción viable si tenemos algunos idiomas disponibles.

Mini proyecto de Twitter

En el presente caso, primero debemos limpiar los datos no estructurados y luego convertirlos en una matriz de datos para aplicar el modelado de temas en ellos. En general, al obtener datos de Twitter, hay varios caracteres que no nos interesa utilizar, al menos en la primera etapa del proceso de limpieza de datos.

Por ejemplo, después de obtener los tweets, obtenemos estos caracteres extraños: “<ed><U+00A0><U+00BD><ed><U+00B8><U+008B>”. Estos son probablemente emoticones, por lo que para limpiar los datos, simplemente los eliminaremos usando el siguiente script. Este código también está disponible en el archivo bda/part1/collect_data/cleaning_data.R.

rm(list = ls(all = TRUE)); gc() # Clears the global environment

source('collect_data_twitter.R')

# Some tweets

head(df$text)

[1] "I’m not a big fan of turkey but baked Mac &

cheese <ed><U+00A0><U+00BD><ed><U+00B8><U+008B>"

[2] "@Jayoh30 Like no special sauce on a big mac. HOW"

### We are interested in the text - Let’s clean it!

# We first convert the encoding of the text from latin1 to ASCII

df$text <- sapply(df$text,function(row) iconv(row, "latin1", "ASCII", sub = ""))

# Create a function to clean tweets

clean.text <- function(tx) {

tx <- gsub("htt.{1,20}", " ", tx, ignore.case = TRUE)

tx = gsub("[^#[:^punct:]]|@|RT", " ", tx, perl = TRUE, ignore.case = TRUE)

tx = gsub("[[:digit:]]", " ", tx, ignore.case = TRUE)

tx = gsub(" {1,}", " ", tx, ignore.case = TRUE)

tx = gsub("^\\s+|\\s+$", " ", tx, ignore.case = TRUE)

return(tx)

}

clean_tweets <- lapply(df$text, clean.text)

# Cleaned tweets

head(clean_tweets)

[1] " WeNeedFeminlsm MAC s new make up line features men woc and big girls "

[1] " TravelsPhoto What Happens To Your Body One Hour After A Big Mac "

El paso final del mini proyecto de limpieza de datos es tener un texto limpio que podamos convertir en una matriz y aplicarle un algoritmo. Del texto almacenado en el vector clean_tweets podemos convertirlo fácilmente en una matriz de bolsa de palabras y aplicar un algoritmo de aprendizaje no supervisado.

Big Data Analytics – Resumen de datos

La generación de informes es muy importante en el análisis de big data. Toda organización debe tener un suministro regular de información para apoyar su proceso de toma de decisiones. Esta tarea normalmente la manejan analistas de datos con experiencia en SQL y ETL (extracción, transferencia y carga).

El equipo encargado de esta tarea tiene la responsabilidad de difundir la información que se produce en el departamento de análisis de big data a las diferentes áreas de la organización.

El siguiente ejemplo demuestra lo que significa el resumen de datos. Navegue a la carpeta bda/part1/summarize_data y dentro de la carpeta, abra el archivo summary_data.Rproj haciendo doble clic en él. Luego, abra el script summary_data.R y eche un vistazo al código y siga las explicaciones presentadas.

# Install the following packages by running the following code in R.

pkgs = c('data.table', 'ggplot2', 'nycflights13', 'reshape2')

install.packages(pkgs)

El paquete ggplot2 es excelente para la visualización de datos. El paquete data.table es una excelente opción para realizar resúmenes rápidos y eficientes en memoria en R . Un benchmark reciente muestra que es incluso más rápido que pandas , la biblioteca de python utilizada para tareas similares.

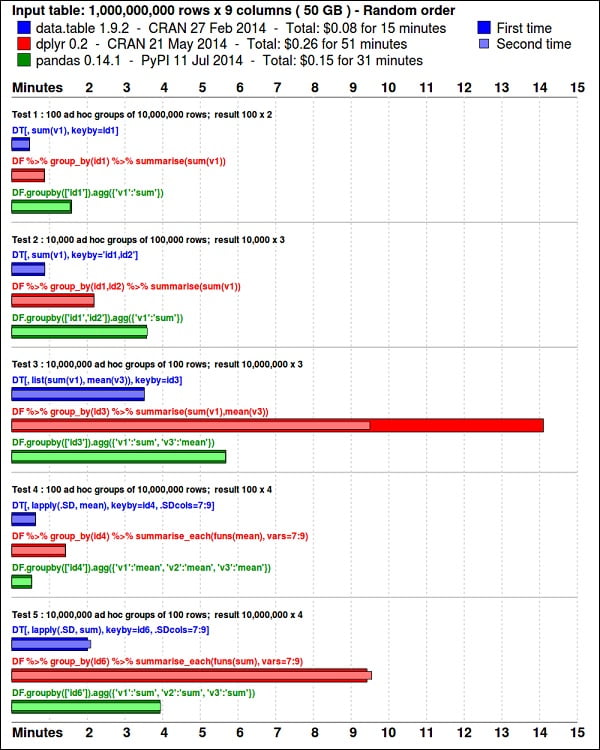
Echa un vistazo a los datos usando el siguiente código. Este código también está disponible en el archivo bda/part1/summarize_data/summarize_data.Rproj .

library(nycflights13)

library(ggplot2)

library(data.table)

library(reshape2)

# Convert the flights data.frame to a data.table object and call it DT

DT <- as.data.table(flights)

# The data has 336776 rows and 16 columns

dim(DT)

# Take a look at the first rows

head(DT)

# year month day dep_time dep_delay arr_time arr_delay carrier

# 1: 2013 1 1 517 2 830 11 UA

# 2: 2013 1 1 533 4 850 20 UA

# 3: 2013 1 1 542 2 923 33 AA

# 4: 2013 1 1 544 -1 1004 -18 B6

# 5: 2013 1 1 554 -6 812 -25 DL

# 6: 2013 1 1 554 -4 740 12 UA

# tailnum flight origin dest air_time distance hour minute

# 1: N14228 1545 EWR IAH 227 1400 5 17

# 2: N24211 1714 LGA IAH 227 1416 5 33

# 3: N619AA 1141 JFK MIA 160 1089 5 42

# 4: N804JB 725 JFK BQN 183 1576 5 44

# 5: N668DN 461 LGA ATL 116 762 5 54

# 6: N39463 1696 EWR ORD 150 719 5 54

El siguiente código tiene un ejemplo de resumen de datos.

### Data Summarization

# Compute the mean arrival delay

DT[, list(mean_arrival_delay = mean(arr_delay, na.rm = TRUE))]

# mean_arrival_delay

# 1: 6.895377

# Now, we compute the same value but for each carrier

mean1 = DT[, list(mean_arrival_delay = mean(arr_delay, na.rm = TRUE)),

by = carrier]

print(mean1)

# carrier mean_arrival_delay

# 1: UA 3.5580111

# 2: AA 0.3642909

# 3: B6 9.4579733

# 4: DL 1.6443409

# 5: EV 15.7964311

# 6: MQ 10.7747334

# 7: US 2.1295951

# 8: WN 9.6491199

# 9: VX 1.7644644

# 10: FL 20.1159055

# 11: AS -9.9308886

# 12: 9E 7.3796692

# 13: F9 21.9207048

# 14: HA -6.9152047

# 15: YV 15.5569853

# 16: OO 11.9310345

# Now let’s compute to means in the same line of code

mean2 = DT[, list(mean_departure_delay = mean(dep_delay, na.rm = TRUE),

mean_arrival_delay = mean(arr_delay, na.rm = TRUE)),

by = carrier]

print(mean2)

# carrier mean_departure_delay mean_arrival_delay

# 1: UA 12.106073 3.5580111

# 2: AA 8.586016 0.3642909

# 3: B6 13.022522 9.4579733

# 4: DL 9.264505 1.6443409

# 5: EV 19.955390 15.7964311

# 6: MQ 10.552041 10.7747334

# 7: US 3.782418 2.1295951

# 8: WN 17.711744 9.6491199

# 9: VX 12.869421 1.7644644

# 10: FL 18.726075 20.1159055

# 11: AS 5.804775 -9.9308886

# 12: 9E 16.725769 7.3796692

# 13: F9 20.215543 21.9207048

# 14: HA 4.900585 -6.9152047

# 15: YV 18.996330 15.5569853

# 16: OO 12.586207 11.9310345

### Create a new variable called gain

# this is the difference between arrival delay and departure delay

DT[, gain:= arr_delay - dep_delay]

# Compute the median gain per carrier

median_gain = DT[, median(gain, na.rm = TRUE), by = carrier]

print(median_gain)

Big Data Analytics – Exploración de datos

El análisis exploratorio de datos es un concepto desarrollado por John Tuckey (1977) que consiste en una nueva perspectiva de la estadística. La idea de Tuckey era que en las estadísticas tradicionales, los datos no se exploraban gráficamente, sino que solo se usaban para probar hipótesis. El primer intento de desarrollar una herramienta se hizo en Stanford, el proyecto se llamó prim9 . La herramienta pudo visualizar datos en nueve dimensiones, por lo tanto, pudo proporcionar una perspectiva multivariada de los datos.

En los últimos días, el análisis exploratorio de datos es imprescindible y se ha incluido en el ciclo de vida del análisis de big data. La capacidad de encontrar información y poder comunicarla de manera efectiva en una organización se alimenta de sólidas capacidades de EDA.

Basado en las ideas de Tuckey, Bell Labs desarrolló el lenguaje de programación S para proporcionar una interfaz interactiva para hacer estadísticas. La idea de S era proporcionar amplias capacidades gráficas con un lenguaje fácil de usar. En el mundo actual, en el contexto de Big Data, R , que se basa en el lenguaje de programación S , es el software de análisis más popular.

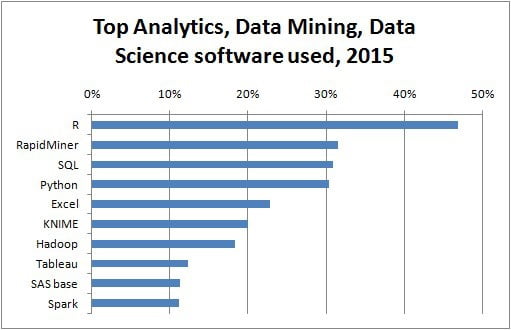
El siguiente programa demuestra el uso del análisis exploratorio de datos.

El siguiente es un ejemplo de análisis exploratorio de datos. Este código también está disponible en el archivo part1/eda/exploratory_data_analysis.R .

library(nycflights13)

library(ggplot2)

library(data.table)

library(reshape2)

# Using the code from the previous section

# This computes the mean arrival and departure delays by carrier.

DT <- as.data.table(flights)

mean2 = DT[, list(mean_departure_delay = mean(dep_delay, na.rm = TRUE),

mean_arrival_delay = mean(arr_delay, na.rm = TRUE)),

by = carrier]

# In order to plot data in R usign ggplot, it is normally needed to reshape the data

# We want to have the data in long format for plotting with ggplot

dt = melt(mean2, id.vars = ’carrier’)

# Take a look at the first rows

print(head(dt))

# Take a look at the help for ?geom_point and geom_line to find similar examples

# Here we take the carrier code as the x axis

# the value from the dt data.table goes in the y axis

# The variable column represents the color

p = ggplot(dt, aes(x = carrier, y = value, color = variable, group = variable)) +

geom_point() + # Plots points

geom_line() + # Plots lines

theme_bw() + # Uses a white background

labs(list(title = 'Mean arrival and departure delay by carrier',

x = 'Carrier', y = 'Mean delay'))

print(p)

# Save the plot to disk

ggsave('mean_delay_by_carrier.png', p,

width = 10.4, height = 5.07)

El código debe producir una imagen como la siguiente:

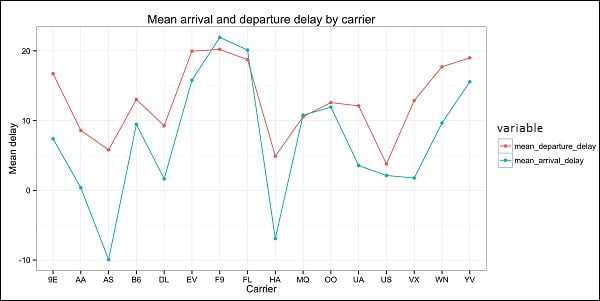
Big Data Analytics – Visualización de datos

Para comprender los datos, a menudo es útil visualizarlos. Normalmente, en las aplicaciones de Big Data, el interés se basa en encontrar información en lugar de simplemente hacer gráficos hermosos. Los siguientes son ejemplos de diferentes enfoques para comprender los datos mediante gráficos.

Para empezar a analizar los datos de los vuelos, podemos empezar comprobando si existen correlaciones entre las variables numéricas. Este código también está disponible en el archivo bda/part1/data_visualization/data_visualization.R .

# Install the package corrplot by running

install.packages('corrplot')

# then load the library

library(corrplot)

# Load the following libraries

library(nycflights13)

library(ggplot2)

library(data.table)

library(reshape2)

# We will continue working with the flights data

DT <- as.data.table(flights)

head(DT) # take a look

# We select the numeric variables after inspecting the first rows.

numeric_variables = c('dep_time', 'dep_delay',

'arr_time', 'arr_delay', 'air_time', 'distance')

# Select numeric variables from the DT data.table

dt_num = DT[, numeric_variables, with = FALSE]

# Compute the correlation matrix of dt_num

cor_mat = cor(dt_num, use = "complete.obs")

print(cor_mat)

### Here is the correlation matrix

# dep_time dep_delay arr_time arr_delay air_time distance

# dep_time 1.00000000 0.25961272 0.66250900 0.23230573 -0.01461948 -0.01413373

# dep_delay 0.25961272 1.00000000 0.02942101 0.91480276 -0.02240508 -0.02168090

# arr_time 0.66250900 0.02942101 1.00000000 0.02448214 0.05429603 0.04718917

# arr_delay 0.23230573 0.91480276 0.02448214 1.00000000 -0.03529709 -0.06186776

# air_time -0.01461948 -0.02240508 0.05429603 -0.03529709 1.00000000 0.99064965

# distance -0.01413373 -0.02168090 0.04718917 -0.06186776 0.99064965 1.00000000

# We can display it visually to get a better understanding of the data

corrplot.mixed(cor_mat, lower = "circle", upper = "ellipse")

# save it to disk

png('corrplot.png')

print(corrplot.mixed(cor_mat, lower = "circle", upper = "ellipse"))

dev.off()

Este código genera la siguiente visualización de matriz de correlación:

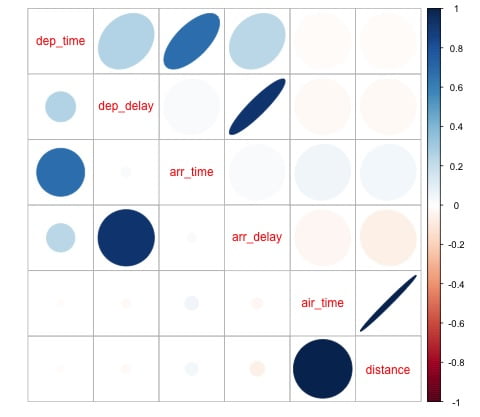
Podemos ver en el gráfico que existe una fuerte correlación entre algunas de las variables en el conjunto de datos. Por ejemplo, la demora en la llegada y la demora en la salida parecen estar altamente correlacionadas. Podemos ver esto porque la elipse muestra una relación casi lineal entre ambas variables, sin embargo, no es sencillo encontrar causalidad a partir de este resultado.

No podemos decir que como dos variables están correlacionadas, una tiene un efecto sobre la otra. También encontramos en la gráfica una fuerte correlación entre el tiempo de aire y la distancia, lo cual es bastante razonable de esperar ya que con más distancia, el tiempo de vuelo debería crecer.

También podemos hacer análisis univariados de los datos. Una forma simple y efectiva de visualizar las distribuciones son los diagramas de caja . El siguiente código demuestra cómo producir diagramas de caja y diagramas de Trellis usando la biblioteca ggplot2. Este código también está disponible en el archivo bda/part1/data_visualization/boxplots.R .

source('data_visualization.R')

### Analyzing Distributions using box-plots

# The following shows the distance as a function of the carrier

p = ggplot(DT, aes(x = carrier, y = distance, fill = carrier)) + # Define the carrier

in the x axis and distance in the y axis

geom_box-plot() + # Use the box-plot geom

theme_bw() + # Leave a white background - More in line with tufte's

principles than the default

guides(fill = FALSE) + # Remove legend

labs(list(title = 'Distance as a function of carrier', # Add labels

x = 'Carrier', y = 'Distance'))

p

# Save to disk

png(‘boxplot_carrier.png’)

print(p)

dev.off()

# Let's add now another variable, the month of each flight

# We will be using facet_wrap for this

p = ggplot(DT, aes(carrier, distance, fill = carrier)) +

geom_box-plot() +

theme_bw() +

guides(fill = FALSE) +

facet_wrap(~month) + # This creates the trellis plot with the by month variable

labs(list(title = 'Distance as a function of carrier by month',

x = 'Carrier', y = 'Distance'))

p

# The plot shows there aren't clear differences between distance in different months

# Save to disk

png('boxplot_carrier_by_month.png')

print(p)

dev.off()

Análisis de Big Data – Introducción a R

Esta sección está dedicada a presentar a los usuarios el lenguaje de programación R. R se puede descargar desde el sitio web de cran . Para usuarios de Windows, es útil instalar rtools y el IDE de rstudio .

El concepto general detrás de R es servir como interfaz para otro software desarrollado en lenguajes compilados como C, C++ y Fortran y brindar al usuario una herramienta interactiva para analizar datos.

Navegue a la carpeta del archivo zip del libro bda/part2/R_introduction y abra el archivo R_introduction.Rproj . Esto abrirá una sesión de RStudio. Luego abra el archivo 01_vectors.R. Ejecute el script línea por línea y siga los comentarios en el código. Otra opción útil para aprender es simplemente escribir el código, esto te ayudará a acostumbrarte a la sintaxis de R. En R los comentarios se escriben con el símbolo #.

Para mostrar los resultados de ejecutar el código R en el libro, después de evaluar el código, se comentan los resultados que devuelve R. De esta forma, puedes copiar y pegar el código en el libro y probar directamente secciones del mismo en R.

# Create a vector of numbers

numbers = c(1, 2, 3, 4, 5)

print(numbers)

# [1] 1 2 3 4 5

# Create a vector of letters

ltrs = c('a', 'b', 'c', 'd', 'e')

# [1] "a" "b" "c" "d" "e"

# Concatenate both

mixed_vec = c(numbers, ltrs)

print(mixed_vec)

# [1] "1" "2" "3" "4" "5" "a" "b" "c" "d" "e"

Analicemos lo que sucedió en el código anterior. Podemos ver que es posible crear vectores con números y con letras. No necesitábamos decirle a R qué tipo de tipo de datos queríamos de antemano. Finalmente, pudimos crear un vector con números y letras. El vector mixed_vec ha forzado los números a carácter, podemos ver esto al visualizar cómo los valores se imprimen entre comillas.

El siguiente código muestra el tipo de datos de diferentes vectores según lo devuelto por la clase de función. Es común usar la función de clase para “interrogar” a un objeto, preguntándole cuál es su clase.

### Evaluate the data types using class

### One dimensional objects

# Integer vector

num = 1:10

class(num)

# [1] "integer"

# Numeric vector, it has a float, 10.5

num = c(1:10, 10.5)

class(num)

# [1] "numeric"

# Character vector

ltrs = letters[1:10]

class(ltrs)

# [1] "character"

# Factor vector

fac = as.factor(ltrs)

class(fac)

# [1] "factor"

R también admite objetos bidimensionales. En el siguiente código, hay ejemplos de las dos estructuras de datos más populares utilizadas en R: la matriz y el marco de datos.

# Matrix

M = matrix(1:12, ncol = 4)

# [,1] [,2] [,3] [,4]

# [1,] 1 4 7 10

# [2,] 2 5 8 11

# [3,] 3 6 9 12

lM = matrix(letters[1:12], ncol = 4)

# [,1] [,2] [,3] [,4]

# [1,] "a" "d" "g" "j"

# [2,] "b" "e" "h" "k"

# [3,] "c" "f" "i" "l"

# Coerces the numbers to character

# cbind concatenates two matrices (or vectors) in one matrix

cbind(M, lM)

# [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]

# [1,] "1" "4" "7" "10" "a" "d" "g" "j"

# [2,] "2" "5" "8" "11" "b" "e" "h" "k"

# [3,] "3" "6" "9" "12" "c" "f" "i" "l"

class(M)

# [1] "matrix"

class(lM)

# [1] "matrix"

# data.frame

# One of the main objects of R, handles different data types in the same object.

# It is possible to have numeric, character and factor vectors in the same data.frame

df = data.frame(n = 1:5, l = letters[1:5])

df

# n l

# 1 1 a

# 2 2 b

# 3 3 c

# 4 4 d

# 5 5 e

Como se demostró en el ejemplo anterior, es posible utilizar diferentes tipos de datos en el mismo objeto. En general, así es como se presentan los datos en las bases de datos, las API, parte de los datos son texto o vectores de caracteres y otros numéricos. El trabajo del analista es determinar qué tipo de datos estadísticos asignar y luego usar el tipo de datos R correcto para ello. En estadística, normalmente consideramos que las variables son de los siguientes tipos:

• Numérico
• Nominal o categórico
• Ordinal

En R, un vector puede ser de las siguientes clases:

• Numérico – Entero
• Factor
• factor ordenado

R proporciona un tipo de datos para cada tipo estadístico de variable. Sin embargo, el factor ordenado rara vez se usa, pero puede ser creado por el factor de función u ordenado.

La siguiente sección trata el concepto de indexación. Esta es una operación bastante común y se ocupa del problema de seleccionar secciones de un objeto y realizar transformaciones en ellas.

# Let's create a data.frame

df = data.frame(numbers = 1:26, letters)

head(df)

# numbers letters

# 1 1 a

# 2 2 b

# 3 3 c

# 4 4 d

# 5 5 e

# 6 6 f

# str gives the structure of a data.frame, it’s a good summary to inspect an object

str(df)

# 'data.frame': 26 obs. of 2 variables:

# $ numbers: int 1 2 3 4 5 6 7 8 9 10 ...

# $ letters: Factor w/ 26 levels "a","b","c","d",..: 1 2 3 4 5 6 7 8 9 10 ...

# The latter shows the letters character vector was coerced as a factor.

# This can be explained by the stringsAsFactors = TRUE argumnet in data.frame

# read ?data.frame for more information

class(df)

# [1] "data.frame"

### Indexing

# Get the first row

df[1, ]

# numbers letters

# 1 1 a

# Used for programming normally - returns the output as a list

df[1, , drop = TRUE]

# $numbers

# [1] 1

#

# $letters

# [1] a

# Levels: a b c d e f g h i j k l m n o p q r s t u v w x y z

# Get several rows of the data.frame

df[5:7, ]

# numbers letters

# 5 5 e

# 6 6 f

# 7 7 g

### Add one column that mixes the numeric column with the factor column

df$mixed = paste(df$numbers, df$letters, sep = ’’)

str(df)

# 'data.frame': 26 obs. of 3 variables:

# $ numbers: int 1 2 3 4 5 6 7 8 9 10 ...

# $ letters: Factor w/ 26 levels "a","b","c","d",..: 1 2 3 4 5 6 7 8 9 10 ...

# $ mixed : chr "1a" "2b" "3c" "4d" ...

### Get columns

# Get the first column

df[, 1]

# It returns a one dimensional vector with that column

# Get two columns

df2 = df[, 1:2]

head(df2)

# numbers letters

# 1 1 a

# 2 2 b

# 3 3 c

# 4 4 d

# 5 5 e

# 6 6 f

# Get the first and third columns

df3 = df[, c(1, 3)]

df3[1:3, ]

# numbers mixed

# 1 1 1a

# 2 2 2b

# 3 3 3c

### Index columns from their names

names(df)

# [1] "numbers" "letters" "mixed"

# This is the best practice in programming, as many times indeces change, but

variable names don’t

# We create a variable with the names we want to subset

keep_vars = c("numbers", "mixed")

df4 = df[, keep_vars]

head(df4)

# numbers mixed

# 1 1 1a

# 2 2 2b

# 3 3 3c

# 4 4 4d

# 5 5 5e

# 6 6 6f

### subset rows and columns

# Keep the first five rows

df5 = df[1:5, keep_vars]

df5

# numbers mixed

# 1 1 1a

# 2 2 2b

# 3 3 3c

# 4 4 4d

# 5 5 5e

# subset rows using a logical condition

df6 = df[df$numbers < 10, keep_vars]

df6

# numbers mixed

# 1 1 1a

# 2 2 2b

# 3 3 3c

# 4 4 4d

# 5 5 5e

# 6 6 6f

# 7 7 7g

# 8 8 8h

# 9 9 9i

Análisis de Big Data – Introducción a SQL

SQL significa lenguaje de consulta estructurado. Es uno de los lenguajes más utilizados para extraer datos de bases de datos en almacenes de datos tradicionales y tecnologías de big data. Para demostrar los conceptos básicos de SQL, trabajaremos con ejemplos. Para centrarnos en el lenguaje en sí, usaremos SQL dentro de R. En términos de escribir código SQL, esto es exactamente lo que se haría en una base de datos.

El núcleo de SQL son tres declaraciones: SELECT, FROM y WHERE. Los siguientes ejemplos hacen uso de los casos de uso más comunes de SQL. Navegue a la carpeta bda/part2/SQL_introduction y abra el archivo SQL_introduction.Rproj . Luego abra el script 01_select.R. Para escribir código SQL en R, necesitamos instalar el paquete sqldf como se muestra en el siguiente código.

# Install the sqldf package

install.packages('sqldf')

# load the library

library('sqldf')

library(nycflights13)

# We will be working with the fligths dataset in order to introduce SQL

# Let’s take a look at the table

str(flights)

# Classes 'tbl_d', 'tbl' and 'data.frame': 336776 obs. of 16 variables:

# $ year : int 2013 2013 2013 2013 2013 2013 2013 2013 2013 2013 ...

# $ month : int 1 1 1 1 1 1 1 1 1 1 ...

# $ day : int 1 1 1 1 1 1 1 1 1 1 ...

# $ dep_time : int 517 533 542 544 554 554 555 557 557 558 ...

# $ dep_delay: num 2 4 2 -1 -6 -4 -5 -3 -3 -2 ...

# $ arr_time : int 830 850 923 1004 812 740 913 709 838 753 ...

# $ arr_delay: num 11 20 33 -18 -25 12 19 -14 -8 8 ...

# $ carrier : chr "UA" "UA" "AA" "B6" ...

# $ tailnum : chr "N14228" "N24211" "N619AA" "N804JB" ...

# $ flight : int 1545 1714 1141 725 461 1696 507 5708 79 301 ...

# $ origin : chr "EWR" "LGA" "JFK" "JFK" ...

# $ dest : chr "IAH" "IAH" "MIA" "BQN" ...

# $ air_time : num 227 227 160 183 116 150 158 53 140 138 ...

# $ distance : num 1400 1416 1089 1576 762 ...

# $ hour : num 5 5 5 5 5 5 5 5 5 5 ...

# $ minute : num 17 33 42 44 54 54 55 57 57 58 ...

La declaración de selección se usa para recuperar columnas de tablas y hacer cálculos sobre ellas. La instrucción SELECT más simple se muestra en ej1 . También podemos crear nuevas variables como se muestra en ej2 .

### SELECT statement

ej1 = sqldf("

SELECT

dep_time

,dep_delay

,arr_time

,carrier

,tailnum

FROM

flights

")

head(ej1)

# dep_time dep_delay arr_time carrier tailnum

# 1 517 2 830 UA N14228

# 2 533 4 850 UA N24211

# 3 542 2 923 AA N619AA

# 4 544 -1 1004 B6 N804JB

# 5 554 -6 812 DL N668DN

# 6 554 -4 740 UA N39463

# In R we can use SQL with the sqldf function. It works exactly the same as in

a database

# The data.frame (in this case flights) represents the table we are querying

and goes in the FROM statement

# We can also compute new variables in the select statement using the syntax:

# old_variables as new_variable

ej2 = sqldf("

SELECT

arr_delay - dep_delay as gain,

carrier

FROM

flights

")

ej2[1:5, ]

# gain carrier

# 1 9 UA

# 2 16 UA

# 3 31 AA

# 4 -17 B6

# 5 -19 DL

Una de las características más comunes de SQL es el grupo por declaración. Esto permite calcular un valor numérico para diferentes grupos de otra variable. Abra el script 02_group_by.R.

### GROUP BY

# Computing the average

ej3 = sqldf("

SELECT

avg(arr_delay) as mean_arr_delay,

avg(dep_delay) as mean_dep_delay,

carrier

FROM

flights

GROUP BY

carrier

")

# mean_arr_delay mean_dep_delay carrier

# 1 7.3796692 16.725769 9E

# 2 0.3642909 8.586016 AA

# 3 -9.9308886 5.804775 AS

# 4 9.4579733 13.022522 B6

# 5 1.6443409 9.264505 DL

# 6 15.7964311 19.955390 EV

# 7 21.9207048 20.215543 F9

# 8 20.1159055 18.726075 FL

# 9 -6.9152047 4.900585 HA

# 10 10.7747334 10.552041 MQ

# 11 11.9310345 12.586207 OO

# 12 3.5580111 12.106073 UA

# 13 2.1295951 3.782418 US

# 14 1.7644644 12.869421 VX

# 15 9.6491199 17.711744 WN

# 16 15.5569853 18.996330 YV

# Other aggregations

ej4 = sqldf("

SELECT

avg(arr_delay) as mean_arr_delay,

min(dep_delay) as min_dep_delay,

max(dep_delay) as max_dep_delay,

carrier

FROM

flights

GROUP BY

carrier

")

# We can compute the minimun, mean, and maximum values of a numeric value

ej4

# mean_arr_delay min_dep_delay max_dep_delay carrier

# 1 7.3796692 -24 747 9E

# 2 0.3642909 -24 1014 AA

# 3 -9.9308886 -21 225 AS

# 4 9.4579733 -43 502 B6

# 5 1.6443409 -33 960 DL

# 6 15.7964311 -32 548 EV

# 7 21.9207048 -27 853 F9

# 8 20.1159055 -22 602 FL

# 9 -6.9152047 -16 1301 HA

# 10 10.7747334 -26 1137 MQ

# 11 11.9310345 -14 154 OO

# 12 3.5580111 -20 483 UA

# 13 2.1295951 -19 500 US

# 14 1.7644644 -20 653 VX

# 15 9.6491199 -13 471 WN

# 16 15.5569853 -16 387 YV

### We could be also interested in knowing how many observations each carrier has

ej5 = sqldf("

SELECT

carrier, count(*) as count

FROM

flights

GROUP BY

carrier

")

ej5

# carrier count

# 1 9E 18460

# 2 AA 32729

# 3 AS 714

# 4 B6 54635

# 5 DL 48110

# 6 EV 54173

# 7 F9 685

# 8 FL 3260

# 9 HA 342

# 10 MQ 26397

# 11 OO 32

# 12 UA 58665

# 13 US 20536

# 14 VX 5162

# 15 WN 12275

# 16 YV 601

La característica más útil de SQL son las uniones. Una unión significa que queremos combinar la tabla A y la tabla B en una tabla usando una columna para hacer coincidir los valores de ambas tablas. Existen diferentes tipos de joins, en términos prácticos, para empezar estos serán los más útiles: inner join y left outside join.

# Let’s create two tables: A and B to demonstrate joins.

A = data.frame(c1 = 1:4, c2 = letters[1:4])

B = data.frame(c1 = c(2,4,5,6), c2 = letters[c(2:5)])

A

# c1 c2

# 1 a

# 2 b

# 3 c

# 4 d

B

# c1 c2

# 2 b

# 4 c

# 5 d

# 6 e

### INNER JOIN

# This means to match the observations of the column we would join the tables by.

inner = sqldf("

SELECT

A.c1, B.c2

FROM

A INNER JOIN B

ON A.c1 = B.c1

")

# Only the rows that match c1 in both A and B are returned

inner

# c1 c2

# 2 b

# 4 c

### LEFT OUTER JOIN

# the left outer join, sometimes just called left join will return the

# first all the values of the column used from the A table

left = sqldf("

SELECT

A.c1, B.c2

FROM

A LEFT OUTER JOIN B

ON A.c1 = B.c1

")

# Only the rows that match c1 in both A and B are returned

left

# c1 c2

# 1 <NA>

# 2 b

# 3 <NA>

# 4 c

Big Data Analytics – Cuadros y gráficos

El primer enfoque para analizar datos es analizarlos visualmente. Los objetivos al hacer esto normalmente son encontrar relaciones entre variables y descripciones univariadas de las variables. Podemos dividir estas estrategias como −

• Análisis univariado
• Analisis multivariable

Métodos gráficos univariados

Univariante es un término estadístico. En la práctica, significa que queremos analizar una variable independientemente del resto de los datos. Las parcelas que permiten hacer esto de manera eficiente son:

diagramas de caja

Los diagramas de caja se utilizan normalmente para comparar distribuciones. Es una excelente manera de inspeccionar visualmente si hay diferencias entre las distribuciones. Podemos ver si hay diferencias entre el precio de los diamantes para diferentes cortes.

# We will be using the ggplot2 library for plotting

library(ggplot2)

data("diamonds")

# We will be using the diamonds dataset to analyze distributions of numeric variables

head(diamonds)

# carat cut color clarity depth table price x y z

# 1 0.23 Ideal E SI2 61.5 55 326 3.95 3.98 2.43

# 2 0.21 Premium E SI1 59.8 61 326 3.89 3.84 2.31

# 3 0.23 Good E VS1 56.9 65 327 4.05 4.07 2.31

# 4 0.29 Premium I VS2 62.4 58 334 4.20 4.23 2.63

# 5 0.31 Good J SI2 63.3 58 335 4.34 4.35 2.75

# 6 0.24 Very Good J VVS2 62.8 57 336 3.94 3.96 2.48

### Box-Plots

p = ggplot(diamonds, aes(x = cut, y = price, fill = cut)) +

geom_box-plot() +

theme_bw()

print(p)

Podemos ver en el gráfico que hay diferencias en la distribución del precio de los diamantes en diferentes tipos de corte.

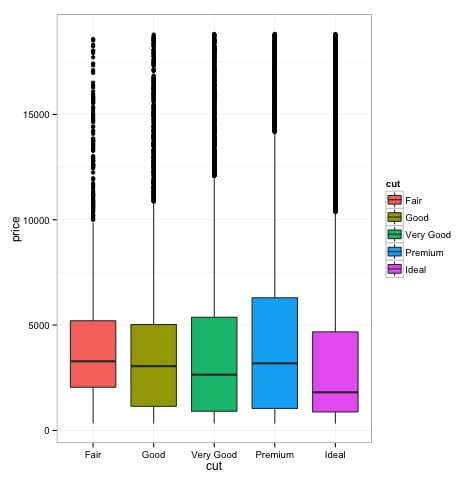
Histogramas

source('01_box_plots.R')

# We can plot histograms for each level of the cut factor variable using

facet_grid

p = ggplot(diamonds, aes(x = price, fill = cut)) +

geom_histogram() +

facet_grid(cut ~ .) +

theme_bw()

p

# the previous plot doesn’t allow to visuallize correctly the data because of

the differences in scale

# we can turn this off using the scales argument of facet_grid

p = ggplot(diamonds, aes(x = price, fill = cut)) +

geom_histogram() +

facet_grid(cut ~ ., scales = 'free') +

theme_bw()

p

png('02_histogram_diamonds_cut.png')

print(p)

dev.off()

La salida del código anterior será la siguiente:

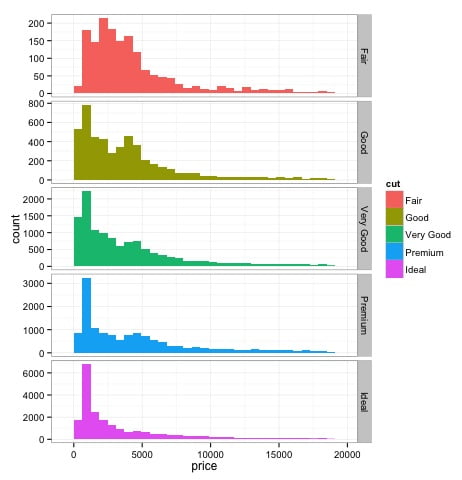
Métodos gráficos multivariados

Los métodos gráficos multivariados en el análisis exploratorio de datos tienen el objetivo de encontrar relaciones entre diferentes variables. Hay dos formas de lograr esto que se usan comúnmente: graficar una matriz de correlación de variables numéricas o simplemente graficar los datos sin procesar como una matriz de diagramas de dispersión.

Para demostrar esto, utilizaremos el conjunto de datos de diamantes. Para seguir el código, abra el script bda/part2/charts/03_multivariate_analysis.R .

library(ggplot2)

data(diamonds)

# Correlation matrix plots

keep_vars = c('carat', 'depth', 'price', 'table')

df = diamonds[, keep_vars]

# compute the correlation matrix

M_cor = cor(df)

# carat depth price table

# carat 1.00000000 0.02822431 0.9215913 0.1816175

# depth 0.02822431 1.00000000 -0.0106474 -0.2957785

# price 0.92159130 -0.01064740 1.0000000 0.1271339

# table 0.18161755 -0.29577852 0.1271339 1.0000000

# plots

heat-map(M_cor)

El código producirá el siguiente resultado:

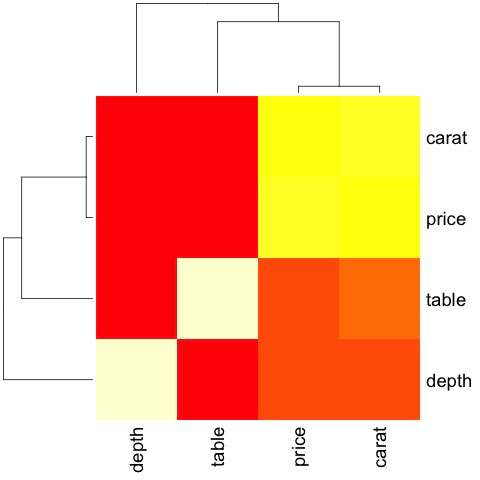
Esto es un resumen, nos dice que hay una fuerte correlación entre el precio y el signo de intercalación, y no mucho entre las otras variables.

Una matriz de correlación puede ser útil cuando tenemos una gran cantidad de variables, en cuyo caso no sería práctico graficar los datos sin procesar. Como se mencionó, también es posible mostrar los datos sin procesar:

library(GGally)

ggpairs(df)

Podemos ver en el gráfico que se confirman los resultados mostrados en el mapa de calor, hay una correlación de 0,922 entre las variables precio y quilates.

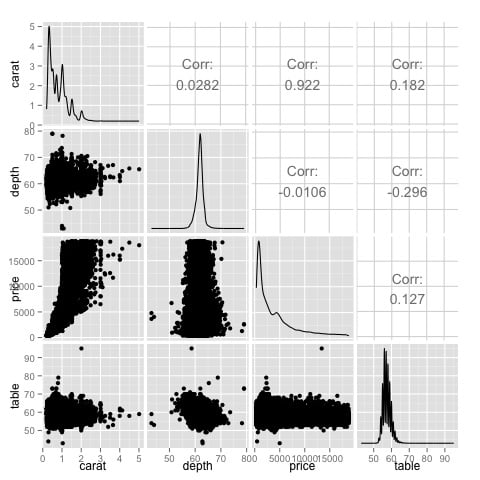
Es posible visualizar esta relación en el gráfico de dispersión precio-quilate ubicado en el índice (3, 1) de la matriz del gráfico de dispersión.

Big Data Analytics – Herramientas de análisis de datos

Hay una variedad de herramientas que permiten a un científico de datos analizar datos de manera efectiva. Normalmente, el aspecto de ingeniería del análisis de datos se centra en las bases de datos, el científico de datos se centra en herramientas que pueden implementar productos de datos. La siguiente sección analiza las ventajas de diferentes herramientas con un enfoque en los paquetes estadísticos que los científicos de datos usan en la práctica con mayor frecuencia.

Lenguaje de programación R

R es un lenguaje de programación de código abierto centrado en el análisis estadístico. Es competitivo con herramientas comerciales como SAS, SPSS en términos de capacidades estadísticas. Se piensa que es una interfaz para otros lenguajes de programación como C, C++ o Fortran.

Otra ventaja de R es la gran cantidad de bibliotecas de código abierto disponibles. En CRAN hay más de 6000 paquetes que se pueden descargar gratis y en Github hay una gran variedad de paquetes R disponibles.

En términos de rendimiento, R es lento para operaciones intensivas, dada la gran cantidad de bibliotecas disponibles, las secciones lentas del código están escritas en lenguajes compilados. Pero si tiene la intención de realizar operaciones que requieren escritura profunda para bucles, entonces R no sería su mejor alternativa. Para fines de análisis de datos, existen buenas bibliotecas como data.table, glmnet, ranger, xgboost, ggplot2, caret que permiten usar R como una interfaz para lenguajes de programación más rápidos.

Python para el análisis de datos

Python es un lenguaje de programación de propósito general y contiene una cantidad importante de bibliotecas dedicadas al análisis de datos, como pandas, scikit-learn, theano, numpy y scipy .

La mayor parte de lo que está disponible en R también se puede hacer en Python, pero descubrimos que R es más fácil de usar. En caso de que esté trabajando con grandes conjuntos de datos, normalmente Python es una mejor opción que R. Python se puede usar de manera bastante efectiva para limpiar y procesar datos línea por línea. Esto es posible desde R, pero no es tan eficiente como Python para tareas de secuencias de comandos.

Para el aprendizaje automático, scikit-learn es un buen entorno que tiene disponible una gran cantidad de algoritmos que pueden manejar conjuntos de datos de tamaño mediano sin problemas. En comparación con la biblioteca equivalente de R (caret), scikit-learn tiene una API más limpia y consistente.

julia

Julia es un lenguaje de programación dinámico de alto nivel y alto rendimiento para computación técnica. Su sintaxis es bastante similar a R o Python, por lo que si ya está trabajando con R o Python, debería ser bastante sencillo escribir el mismo código en Julia. El idioma es bastante nuevo y ha crecido significativamente en los últimos años, por lo que definitivamente es una opción en este momento.

Recomendaríamos a Julia para la creación de prototipos de algoritmos que son computacionalmente intensivos, como las redes neuronales. Es una gran herramienta para la investigación. En términos de implementar un modelo en producción, probablemente Python tenga mejores alternativas. Sin embargo, esto se está convirtiendo en un problema menor, ya que existen servicios web que realizan la ingeniería de implementación de modelos en R, Python y Julia.

S.A.S.

SAS es un lenguaje comercial que todavía se utiliza para la inteligencia empresarial. Posee un lenguaje base que permite al usuario programar una amplia variedad de aplicaciones. Contiene bastantes productos comerciales que brindan a los usuarios no expertos la capacidad de usar herramientas complejas, como una biblioteca de redes neuronales, sin necesidad de programación.

Más allá de la desventaja obvia de las herramientas comerciales, SAS no se adapta bien a grandes conjuntos de datos. Incluso un conjunto de datos de tamaño mediano tendrá problemas con SAS y hará que el servidor se bloquee. Solo si está trabajando con conjuntos de datos pequeños y los usuarios no son científicos de datos expertos, se recomienda SAS. Para usuarios avanzados, R y Python proporcionan un entorno más productivo.

SPSS

SPSS, actualmente es un producto de IBM para análisis estadístico. Se utiliza principalmente para analizar datos de encuestas y para usuarios que no pueden programar, es una alternativa decente. Probablemente sea tan simple de usar como SAS, pero en términos de implementar un modelo, es más simple ya que proporciona un código SQL para calificar un modelo. Este código normalmente no es eficiente, pero es un comienzo, mientras que SAS vende el producto que califica los modelos para cada base de datos por separado. Para datos pequeños y un equipo sin experiencia, SPSS es una opción tan buena como lo es SAS.

Sin embargo, el software es bastante limitado y los usuarios experimentados serán mucho más productivos con R o Python.

Matlab, octava

Hay otras herramientas disponibles como Matlab o su versión de código abierto (Octave). Estas herramientas se utilizan principalmente para la investigación. En términos de capacidades, R o Python pueden hacer todo lo que está disponible en Matlab u Octave. Solo tiene sentido comprar una licencia del producto si está interesado en el soporte que brindan.

Big Data Analytics – Métodos estadísticos

Al analizar datos, es posible tener un enfoque estadístico. Las herramientas básicas que se necesitan para realizar un análisis básico son:

• Análisis de correlación
• Análisis de variación
• Evaluación de la hipótesis

Cuando se trabaja con grandes conjuntos de datos, no implica ningún problema, ya que estos métodos no son computacionalmente intensivos, con la excepción del análisis de correlación. En este caso, siempre es posible tomar una muestra y los resultados deben ser sólidos.

Análisis de correlación

El análisis de correlación busca encontrar relaciones lineales entre variables numéricas. Esto puede ser útil en diferentes circunstancias. Un uso común es el análisis exploratorio de datos, en la sección 16.0.2 del libro hay un ejemplo básico de este enfoque. En primer lugar, la métrica de correlación utilizada en el ejemplo mencionado se basa en el coeficiente de Pearson . Sin embargo, existe otra métrica de correlación interesante que no se ve afectada por los valores atípicos. Esta métrica se llama correlación de Spearman.

La métrica de correlación de Spearman es más resistente a la presencia de valores atípicos que el método de Pearson y ofrece mejores estimaciones de las relaciones lineales entre variables numéricas cuando los datos no se distribuyen normalmente.

library(ggplot2)

# Select variables that are interesting to compare pearson and spearman

correlation methods.

x = diamonds[, c('x', 'y', 'z', 'price')]

# From the histograms we can expect differences in the correlations of both

metrics.

# In this case as the variables are clearly not normally distributed, the

spearman correlation

# is a better estimate of the linear relation among numeric variables.

par(mfrow = c(2,2))

colnm = names(x)

for(i in 1:4) {

hist(x[[i]], col = 'deepskyblue3', main = sprintf('Histogram of %s', colnm[i]))

}

par(mfrow = c(1,1))

De los histogramas en la siguiente figura, podemos esperar diferencias en las correlaciones de ambas métricas. En este caso, como las variables claramente no tienen una distribución normal, la correlación de Spearman es una mejor estimación de la relación lineal entre las variables numéricas.

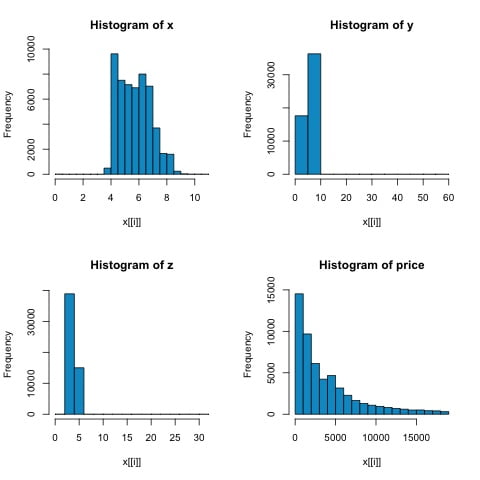
Para calcular la correlación en R, abra el archivo bda/part2/statistical_methods/correlation/correlation.R que tiene esta sección de código.

## Correlation Matrix - Pearson and spearman

cor_pearson <- cor(x, method = 'pearson')

cor_spearman <- cor(x, method = 'spearman')

### Pearson Correlation

print(cor_pearson)

# x y z price

# x 1.0000000 0.9747015 0.9707718 0.8844352

# y 0.9747015 1.0000000 0.9520057 0.8654209

# z 0.9707718 0.9520057 1.0000000 0.8612494

# price 0.8844352 0.8654209 0.8612494 1.0000000

### Spearman Correlation

print(cor_spearman)

# x y z price

# x 1.0000000 0.9978949 0.9873553 0.9631961

# y 0.9978949 1.0000000 0.9870675 0.9627188

# z 0.9873553 0.9870675 1.0000000 0.9572323

# price 0.9631961 0.9627188 0.9572323 1.0000000

Prueba de chi-cuadrado

La prueba de chi-cuadrado nos permite probar si dos variables aleatorias son independientes. Esto significa que la distribución de probabilidad de cada variable no influye en la otra. Para evaluar la prueba en R, primero debemos crear una tabla de contingencia y luego pasar la tabla a la función chisq.test R.

Por ejemplo, vamos a comprobar si existe una asociación entre las variables: corte y color del conjunto de datos de diamantes. La prueba se define formalmente como −

• H0: La talla variable y el diamante son independientes
• H1: El corte variable y el diamante no son independientes

Asumiríamos que existe una relación entre estas dos variables por su nombre, pero la prueba puede dar una “regla” objetiva que diga qué tan significativo es o no este resultado.

En el siguiente fragmento de código, encontramos que el valor p de la prueba es 2.2e-16, esto es casi cero en términos prácticos. Luego, después de ejecutar la prueba con una simulación de Monte Carlo , encontramos que el valor p es 0.0004998, que aún es bastante más bajo que el umbral de 0.05. Este resultado significa que rechazamos la hipótesis nula (H0), por lo que creemos que las variables corte y color no son independientes.

library(ggplot2)

# Use the table function to compute the contingency table

tbl = table(diamonds$cut, diamonds$color)

tbl

# D E F G H I J

# Fair 163 224 312 314 303 175 119

# Good 662 933 909 871 702 522 307

# Very Good 1513 2400 2164 2299 1824 1204 678

# Premium 1603 2337 2331 2924 2360 1428 808

# Ideal 2834 3903 3826 4884 3115 2093 896

# In order to run the test we just use the chisq.test function.

chisq.test(tbl)

# Pearson’s Chi-squared test

# data: tbl

# X-squared = 310.32, df = 24, p-value < 2.2e-16

# It is also possible to compute the p-values using a monte-carlo simulation

# It's needed to add the simulate.p.value = TRUE flag and the amount of

simulations

chisq.test(tbl, simulate.p.value = TRUE, B = 2000)

# Pearson’s Chi-squared test with simulated p-value (based on 2000 replicates)

# data: tbl

# X-squared = 310.32, df = NA, p-value = 0.0004998

prueba t

La idea de la prueba t es evaluar si hay diferencias en la distribución de una variable numérica # entre diferentes grupos de una variable nominal. Para demostrar esto, seleccionaré los niveles Justo e Ideal del corte de la variable factorial, luego compararemos los valores de una variable numérica entre esos dos grupos.

data = diamonds[diamonds$cut %in% c('Fair', 'Ideal'), ]

data$cut = droplevels.factor(data$cut) # Drop levels that aren’t used from the

cut variable

df1 = data[, c('cut', 'price')]

# We can see the price means are different for each group

tapply(df1$price, df1$cut, mean)

# Fair Ideal

# 4358.758 3457.542

Las pruebas t se implementan en R con la función t.test . La interfaz de fórmula para t.test es la forma más sencilla de usarla, la idea es que una variable numérica se explique mediante una variable de grupo.

Por ejemplo: t.test(numeric_variable ~ group_variable, data = data) . En el ejemplo anterior, numeric_variable es price y group_variable es cut .

Desde una perspectiva estadística, estamos probando si existen diferencias en las distribuciones de la variable numérica entre dos grupos. Formalmente la prueba de hipótesis se describe con una hipótesis nula (H0) y una hipótesis alternativa (H1).

• H0: No hay diferencias en las distribuciones de la variable precio entre los grupos Justo e Ideal
• H1 Existen diferencias en las distribuciones de la variable precio entre los grupos Justo e Ideal

Lo siguiente se puede implementar en R con el siguiente código:

t.test(price ~ cut, data = data)

# Welch Two Sample t-test

#

# data: price by cut

# t = 9.7484, df = 1894.8, p-value < 2.2e-16

# alternative hypothesis: true difference in means is not equal to 0

# 95 percent confidence interval:

# 719.9065 1082.5251

# sample estimates:

# mean in group Fair mean in group Ideal

# 4358.758 3457.542

# Another way to validate the previous results is to just plot the

distributions using a box-plot

plot(price ~ cut, data = data, ylim = c(0,12000),

col = 'deepskyblue3')

Podemos analizar el resultado de la prueba comprobando si el valor p es inferior a 0,05. Si este es el caso, mantenemos la hipótesis alternativa. Esto significa que hemos encontrado diferencias de precio entre los dos niveles del factor de corte. Por los nombres de los niveles, habríamos esperado este resultado, pero no habríamos esperado que el precio medio en el grupo Fallido fuera más alto que en el grupo Ideal. Podemos ver esto comparando las medias de cada factor.

El comando plot produce un gráfico que muestra la relación entre el precio y la variable de corte. Es un diagrama de caja; hemos cubierto este gráfico en la sección 16.0.1 pero básicamente muestra la distribución de la variable precio para los dos niveles de corte que estamos analizando.

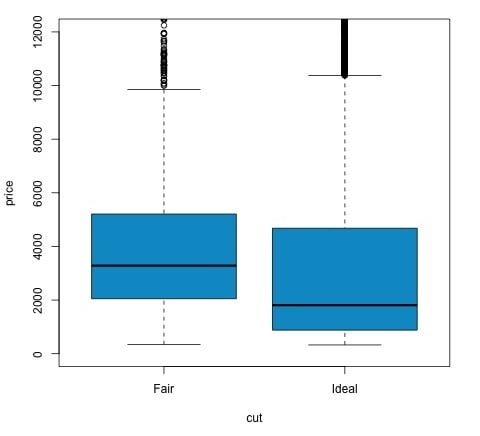
Análisis de variación

El análisis de varianza (ANOVA) es un modelo estadístico utilizado para analizar las diferencias entre la distribución de grupos al comparar la media y la varianza de cada grupo, el modelo fue desarrollado por Ronald Fisher. ANOVA proporciona una prueba estadística de si las medias de varios grupos son iguales o no y, por lo tanto, generaliza la prueba t a más de dos grupos.

Los ANOVA son útiles para comparar la significación estadística de tres o más grupos, ya que realizar múltiples pruebas t de dos muestras aumentaría las posibilidades de cometer un error estadístico de tipo I.

En términos de proporcionar una explicación matemática, se necesita lo siguiente para comprender la prueba.

x _ij = x + (x _yo − x) + (x _ij − x)

Esto conduce al siguiente modelo:

x _ij = μ + α _yo + ∈ _ij

donde μ es la gran media y α _i es la i-ésima media del grupo. Se supone que el término de error ∈ _ij es iid de una distribución normal. La hipótesis nula de la prueba es que −

α1 = α2 ₌ … _= αk

En términos de calcular la estadística de prueba, necesitamos calcular dos valores:

• Suma de cuadrados para la diferencia entre grupos −

SSDB=∑ik∑jnorte(Xi¯¯−X¯)2����=∑��∑��(��¯¯−�¯)2

• Sumas de cuadrados dentro de grupos

SSDW=∑ik∑jnorte(Xyo j¯¯−Xi¯¯)2����=∑��∑��(���¯¯−��¯¯)2

donde SSD _B tiene un grado de libertad de k−1 y SSD _W tiene un grado de libertad de N−k. Luego podemos definir las diferencias cuadráticas medias para cada métrica.

MS _B = SSD _B / (k – 1)

MS _w = SSD _w / (N – k)

Finalmente, la estadística de prueba en ANOVA se define como la relación de las dos cantidades anteriores

F = EM _B / EM _w

que sigue una distribución F con k−1 y N−k grados de libertad. Si la hipótesis nula es verdadera, es probable que F esté cerca de 1. De lo contrario, es probable que el MSB cuadrático medio entre grupos sea grande, lo que da como resultado un valor de F grande.

Básicamente, ANOVA examina las dos fuentes de la varianza total y ve qué parte contribuye más. Por eso se llama análisis de varianza aunque la intención es comparar medias de grupos.

En términos de calcular la estadística, en realidad es bastante simple de hacer en R. El siguiente ejemplo demostrará cómo se hace y trazará los resultados.

library(ggplot2)

# We will be using the mtcars dataset

head(mtcars)

# mpg cyl disp hp drat wt qsec vs am gear carb

# Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4

# Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4

# Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1

# Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1

# Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2

# Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1

# Let's see if there are differences between the groups of cyl in the mpg variable.

data = mtcars[, c('mpg', 'cyl')]

fit = lm(mpg ~ cyl, data = mtcars)

anova(fit)

# Analysis of Variance Table

# Response: mpg

# Df Sum Sq Mean Sq F value Pr(>F)

# cyl 1 817.71 817.71 79.561 6.113e-10 ***

# Residuals 30 308.33 10.28

# Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 .

# Plot the distribution

plot(mpg ~ as.factor(cyl), data = mtcars, col = 'deepskyblue3')

El código producirá el siguiente resultado:

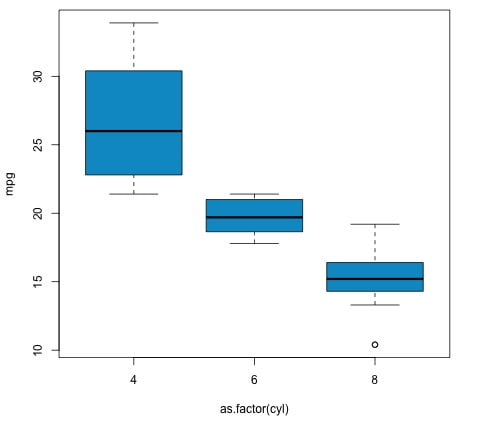
El valor p que obtenemos en el ejemplo es significativamente menor que 0,05, por lo que R devuelve el símbolo ‘***’ para indicarlo. Significa que rechazamos la hipótesis nula y que encontramos diferencias entre las medias de mpg entre los diferentes grupos de la variable cyl .

Aprendizaje automático para el análisis de datos

El aprendizaje automático es un subcampo de la informática que se ocupa de tareas como el reconocimiento de patrones, la visión por computadora, el reconocimiento de voz, el análisis de texto y tiene un fuerte vínculo con las estadísticas y la optimización matemática. Las aplicaciones incluyen el desarrollo de motores de búsqueda, filtrado de spam, reconocimiento óptico de caracteres (OCR), entre otros. Los límites entre la minería de datos, el reconocimiento de patrones y el campo del aprendizaje estadístico no están claros y básicamente todos se refieren a problemas similares.

El aprendizaje automático se puede dividir en dos tipos de tareas:

• Aprendizaje supervisado
• Aprendizaje sin supervisión

Aprendizaje supervisado

El aprendizaje supervisado se refiere a un tipo de problema donde hay un dato de entrada definido como una matriz X y estamos interesados ​​en predecir una respuesta y . Donde X = {x ₁ , x ₂ , …, x _n } tiene n predictores y tiene dos valores y = {c ₁ , c ₂ } .

Una aplicación de ejemplo sería predecir la probabilidad de que un usuario web haga clic en los anuncios utilizando características demográficas como predictores. Esto a menudo se llama para predecir la tasa de clics (CTR). Entonces y = {clic, no − clic} y los predictores podrían ser la dirección IP utilizada, el día que ingresó al sitio, la ciudad del usuario, el país entre otras características que podrían estar disponibles.

Aprendizaje sin supervisión

El aprendizaje no supervisado se ocupa del problema de encontrar grupos que sean similares entre sí sin tener una clase de la que aprender. Hay varios enfoques para la tarea de aprender un mapeo de predictores para encontrar grupos que comparten instancias similares en cada grupo y son diferentes entre sí.

Un ejemplo de aplicación del aprendizaje no supervisado es la segmentación de clientes. Por ejemplo, en la industria de las telecomunicaciones una tarea común es segmentar a los usuarios según el uso que le dan al teléfono. Esto permitiría al departamento de marketing dirigirse a cada grupo con un producto diferente.

Big Data Analytics – Clasificador Naive Bayes

Naive Bayes es una técnica probabilística para construir clasificadores. El supuesto característico del clasificador ingenuo de Bayes es considerar que el valor de una característica particular es independiente del valor de cualquier otra característica, dada la variable de clase.

A pesar de las suposiciones simplificadas mencionadas anteriormente, los clasificadores ingenuos de Bayes tienen buenos resultados en situaciones complejas del mundo real. Una ventaja de Naive Bayes es que solo requiere una pequeña cantidad de datos de entrenamiento para estimar los parámetros necesarios para la clasificación y que el clasificador se puede entrenar de forma incremental.

Naive Bayes es un modelo de probabilidad condicional: dada una instancia de problema a clasificar, representada por un vector x = (x ₁ , …, x _n ) que representa algunas n características (variables independientes), asigna a esta instancia probabilidades para cada uno de K posibles resultados o clases.

pag (Ck|X1, . . . . . ,Xnorte)�(��|�1,…..,��)

El problema con la formulación anterior es que si la cantidad de características n es grande o si una característica puede tomar una gran cantidad de valores, entonces no es factible basar dicho modelo en tablas de probabilidad. Por lo tanto, reformulamos el modelo para hacerlo más simple. Usando el teorema de Bayes, la probabilidad condicional se puede descomponer como −

pag (Ck| x)=pag (Ck) pag ( x |Ck)pag ( x )�(��|�)=�(��)�(�|��)�(�)

Esto significa que bajo los supuestos de independencia anteriores, la distribución condicional sobre la variable de clase C es −

pag (Ck|X1, . . . . . ,Xnorte)=1Zpag (Ck)∏yo = 1nortepag (Xi|Ck)�(��|�1,…..,��)=1��(��)∏�=1��(��|��)

donde la evidencia Z = p( x ) es un factor de escala que depende solo de x ₁ , …, x _n , que es una constante si se conocen los valores de las variables de característica. Una regla común es elegir la hipótesis que sea más probable; esto se conoce como regla de decisión máxima a posteriori o MAP. El clasificador correspondiente, un clasificador de Bayes, es la función que asigna una etiqueta de clase $\hat{y} = C_k$ para algún k de la siguiente manera:y^=Ck�^=��

y^= un r gmx _ _pag (Ck)∏yo = 1nortepag (Xi|Ck)�^=�������(��)∏�=1��(��|��)

La implementación del algoritmo en R es un proceso sencillo. El siguiente ejemplo demuestra cómo entrenar un clasificador Naive Bayes y usarlo para la predicción en un problema de filtrado de spam.

El siguiente script está disponible en el archivo bda/part3/naive_bayes/naive_bayes.R .

# Install these packages

pkgs = c(“klaR”, “caret”, “ElemStatLearn”)

install.packages(pkgs)

library(‘ElemStatLearn’)

library(“klaR”)

library(“caret”)

# Split the data in training and testing

inx = sample(nrow(spam), round(nrow(spam) * 0.9))

train = spam[inx,]

test = spam[-inx,]

# Define a matrix with features, X_train

# And a vector with class labels, y_train

X_train = train[,-58]

y_train = train$spam

X_test = test[,-58]

y_test = test$spam

# Train the model

nb_model = train(X_train, y_train, method = ‘nb’,

trControl = trainControl(method = ‘cv’, number = 3))

# Compute

preds = predict(nb_model$finalModel, X_test)$class

tbl = table(y_test, yhat = preds)

sum(diag(tbl)) / sum(tbl)

# 0.7217391

Como podemos ver en el resultado, la precisión del modelo Naive Bayes es del 72%. Esto significa que el modelo clasifica correctamente el 72% de las instancias.

Análisis de Big Data – Clúster de K-Means

El agrupamiento de k-medias tiene como objetivo dividir n observaciones en k conglomerados en los que cada observación pertenece al conglomerado con la media más cercana, sirviendo como un prototipo del conglomerado. Esto da como resultado una partición del espacio de datos en celdas de Voronoi.

Dado un conjunto de observaciones (x ₁ , x ₂ , …, x _n ) , donde cada observación es un vector real d-dimensional, el agrupamiento de k-medias tiene como objetivo dividir las n observaciones en k grupos G = {G ₁ , G ₂ , …, G _k } para minimizar la suma de cuadrados dentro del grupo (WCSS) definida de la siguiente manera:

un rg _m i n∑yo = 1k∑X∈ _Si∥ x −mi∥2������∑�=1�∑�∈��∥�−��∥2

La última fórmula muestra la función objetivo que se minimiza para encontrar los prototipos óptimos en el agrupamiento de k-medias. La intuición de la fórmula es que nos gustaría encontrar grupos que sean diferentes entre sí y cada miembro de cada grupo debe ser similar a los demás miembros de cada grupo.

El siguiente ejemplo demuestra cómo ejecutar el algoritmo de agrupación en clústeres k-means en R.

library(ggplot2)

# Prepare Data

data = mtcars

# We need to scale the data to have zero mean and unit variance

data <- scale(data)

# Determine number of clusters

wss <- (nrow(data)-1)*sum(apply(data,2,var))

for (i in 2:dim(data)[2]) {

wss[i] <- sum(kmeans(data, centers = i)$withinss)

}

# Plot the clusters

plot(1:dim(data)[2], wss, type = “b”, xlab = “Number of Clusters”,

ylab = “Within groups sum of squares”)

Para encontrar un buen valor para K, podemos trazar la suma de cuadrados dentro de los grupos para diferentes valores de K. Esta métrica normalmente disminuye a medida que se agregan más grupos, nos gustaría encontrar un punto donde la disminución en la suma dentro de los grupos de cuadrados comienza a disminuir lentamente. En la gráfica, este valor está mejor representado por K = 6.

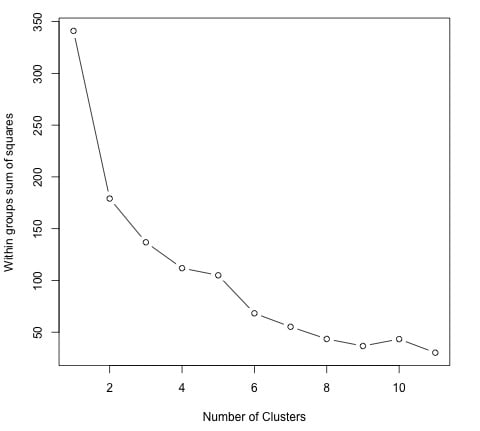
Ahora que se ha definido el valor de K, es necesario ejecutar el algoritmo con ese valor.

# K-Means Cluster Analysis

fit <- kmeans(data, 5) # 5 cluster solution

# get cluster means

aggregate(data,by = list(fit$cluster),FUN = mean)

# append cluster assignment

data <- data.frame(data, fit$cluster)

Big Data Analytics – Reglas de asociación

Sea I = i ₁ , i ₂ , …, i _n un conjunto de n atributos binarios llamados elementos. Sea D = t ₁ , t ₂ , …, t _m ​​un conjunto de transacciones llamado base de datos. Cada transacción en D tiene una ID de transacción única y contiene un subconjunto de los elementos en I. Una regla se define como una implicación de la forma X ⇒ Y donde X, Y ⊆ I y X ∩ Y = ∅.

Los conjuntos de elementos (para conjuntos de elementos cortos) X e Y se denominan antecedente (lado izquierdo o LHS) y consecuente (lado derecho o RHS) de la regla.

Para ilustrar los conceptos, usamos un pequeño ejemplo del dominio del supermercado. El conjunto de artículos es I = {leche, pan, mantequilla, cerveza} y en la siguiente tabla se muestra una pequeña base de datos que contiene los artículos.

Una regla de ejemplo para el supermercado podría ser {leche, pan} ⇒ {mantequilla}, lo que significa que si se compra leche y pan, los clientes también compran mantequilla. Para seleccionar reglas interesantes del conjunto de todas las reglas posibles, se pueden usar restricciones en varias medidas de importancia e interés. Las restricciones más conocidas son los umbrales mínimos de apoyo y confianza.

El soporte de soporte (X) de un conjunto de elementos X se define como la proporción de transacciones en el conjunto de datos que contienen el conjunto de elementos. En la base de datos de ejemplo de la Tabla 1, el conjunto de artículos {leche, pan} tiene un soporte de 2/5 = 0,4 ya que ocurre en el 40 % de todas las transacciones (2 de 5 transacciones). Encontrar conjuntos de elementos frecuentes puede verse como una simplificación del problema de aprendizaje no supervisado.

La confianza de una regla se define conf(X ⇒ Y ) = supp(X ∪ Y )/supp(X). Por ejemplo, la regla {leche, pan} ⇒ {mantequilla} tiene una confianza de 0,2/0,4 = 0,5 en la base de datos de la Tabla 1, lo que significa que para el 50 % de las transacciones que contienen leche y pan, la regla es correcta. La confianza puede interpretarse como una estimación de la probabilidad P(Y|X), la probabilidad de encontrar la RHS de la regla en transacciones bajo la condición de que estas transacciones también contengan la LHS.

En el script ubicado en bda/part3/apriori.R se encuentra el código para implementar el algoritmo apriori .

# Load the library for doing association rules

# install.packages(’arules’)

library(arules)

# Data preprocessing

data(“AdultUCI”)

AdultUCI[1:2,]

AdultUCI[[“fnlwgt”]] <- NULL

AdultUCI[[“education-num”]] <- NULL

AdultUCI[[ “age”]] <- ordered(cut(AdultUCI[[ “age”]], c(15,25,45,65,100)),

labels = c(“Young”, “Middle-aged”, “Senior”, “Old”))

AdultUCI[[ “hours-per-week”]] <- ordered(cut(AdultUCI[[ “hours-per-week”]],

c(0,25,40,60,168)), labels = c(“Part-time”, “Full-time”, “Over-time”, “Workaholic”))

AdultUCI[[ “capital-gain”]] <- ordered(cut(AdultUCI[[ “capital-gain”]],

c(-Inf,0,median(AdultUCI[[ “capital-gain”]][AdultUCI[[ “capitalgain”]]>0]),Inf)),

labels = c(“None”, “Low”, “High”))

AdultUCI[[ “capital-loss”]] <- ordered(cut(AdultUCI[[ “capital-loss”]],

c(-Inf,0, median(AdultUCI[[ “capital-loss”]][AdultUCI[[ “capitalloss”]]>0]),Inf)),

labels = c(“none”, “low”, “high”))

Para generar reglas utilizando el algoritmo a priori, necesitamos crear una matriz de transacciones. El siguiente código muestra cómo hacer esto en R.

# Convert the data into a transactions format

Adult <- as(AdultUCI, “transactions”)

Adult

# transactions in sparse format with

# 48842 transactions (rows) and

# 115 items (columns)

summary(Adult)

# Plot frequent item-sets

itemFrequencyPlot(Adult, support = 0.1, cex.names = 0.8)

# generate rules

min_support = 0.01

confidence = 0.6

rules <- apriori(Adult, parameter = list(support = min_support, confidence = confidence))

rules

inspect(rules[100:110, ])

# lhs rhs support confidence lift

# {occupation = Farming-fishing} => {sex = Male} 0.02856148 0.9362416 1.4005486

# {occupation = Farming-fishing} => {race = White} 0.02831579 0.9281879 1.0855456

# {occupation = Farming-fishing} => {native-country 0.02671881 0.8758389 0.9759474

= United-States}

Big Data Analytics – Árboles de decisión

Un árbol de decisiones es un algoritmo utilizado para problemas de aprendizaje supervisado, como la clasificación o la regresión. Un árbol de decisión o un árbol de clasificación es un árbol en el que cada nodo interno (no hoja) está etiquetado con una característica de entrada. Los arcos que provienen de un nodo etiquetado con una característica se etiquetan con cada uno de los valores posibles de la característica. Cada hoja del árbol está etiquetada con una clase o una distribución de probabilidad sobre las clases.

Un árbol se puede “aprender” dividiendo el conjunto de fuentes en subconjuntos en función de una prueba de valor de atributo. Este proceso se repite en cada subconjunto derivado de manera recursiva denominada partición recursiva . La recursión se completa cuando el subconjunto en un nodo tiene el mismo valor de la variable de destino, o cuando la división ya no agrega valor a las predicciones. Este proceso de inducción descendente de árboles de decisión es un ejemplo de un algoritmo codicioso y es la estrategia más común para aprender árboles de decisión.

Los árboles de decisión utilizados en la minería de datos son de dos tipos principales:

• Árbol de clasificación : cuando la respuesta es una variable nominal, por ejemplo, si un correo electrónico es spam o no.
• Árbol de regresión : cuando el resultado predicho puede considerarse un número real (por ejemplo, el salario de un trabajador).

Los árboles de decisión son un método simple y, como tal, tiene algunos problemas. Uno de estos problemas es la gran variación en los modelos resultantes que producen los árboles de decisión. Para paliar este problema, se desarrollaron métodos conjuntos de árboles de decisión. Hay dos grupos de métodos de conjunto actualmente utilizados ampliamente:

• Árboles de decisión de embolsado : estos árboles se utilizan para crear múltiples árboles de decisión al volver a muestrear repetidamente los datos de entrenamiento con reemplazo y votar los árboles para obtener una predicción de consenso. Este algoritmo ha sido llamado bosque aleatorio.
• Impulsar árboles de decisión : el impulso de gradiente combina aprendices débiles; en este caso, árboles de decisión en un solo alumno fuerte, de forma iterativa. Ajusta un árbol débil a los datos e iterativamente sigue ajustando aprendices débiles para corregir el error del modelo anterior.

# Install the party package

# install.packages(‘party’)

library(party)

library(ggplot2)

head(diamonds)

# We will predict the cut of diamonds using the features available in the

diamonds dataset.

ct = ctree(cut ~ ., data = diamonds)

# plot(ct, main=”Conditional Inference Tree”)

# Example output

# Response: cut

# Inputs: carat, color, clarity, depth, table, price, x, y, z

# Number of observations: 53940

#

# 1) table <= 57; criterion = 1, statistic = 10131.878

# 2) depth <= 63; criterion = 1, statistic = 8377.279

# 3) table <= 56.4; criterion = 1, statistic = 226.423

# 4) z <= 2.64; criterion = 1, statistic = 70.393

# 5) clarity <= VS1; criterion = 0.989, statistic = 10.48

# 6) color <= E; criterion = 0.997, statistic = 12.829

# 7)* weights = 82

# 6) color > E

#Table of prediction errors

table(predict(ct), diamonds$cut)

# Fair Good Very Good Premium Ideal

# Fair 1388 171 17 0 14

# Good 102 2912 499 26 27

# Very Good 54 998 3334 249 355

# Premium 44 711 5054 11915 1167

# Ideal 22 114 3178 1601 19988

# Estimated class probabilities

probs = predict(ct, newdata = diamonds, type = “prob”)

probs = do.call(rbind, probs)

head(probs)

Big Data Analytics – Regresión logística

La regresión logística es un modelo de clasificación en el que la variable de respuesta es categórica. Es un algoritmo que proviene de la estadística y se utiliza para problemas de clasificación supervisada. En regresión logística buscamos encontrar el vector β de parámetros en la siguiente ecuación que minimice la función de costo.

registro _ _yo t (pagi) = l norte (pagi1 -pagi) =β0+β1X1 , yo+ . . . +βkXk , yo�����(��)=��(��1−��)=�0+�1�1,�+…+����,�

El siguiente código demuestra cómo ajustar un modelo de regresión logística en R. Usaremos aquí el conjunto de datos de spam para demostrar la regresión logística, la misma que se usó para Naive Bayes.

De los resultados de las predicciones en términos de precisión, encontramos que el modelo de regresión logra una precisión del 92,5% en el conjunto de prueba, en comparación con el 72% logrado por el clasificador Naive Bayes.

library(ElemStatLearn)

head(spam)

# Split dataset in training and testing

inx = sample(nrow(spam), round(nrow(spam) * 0.8))

train = spam[inx,]

test = spam[-inx,]

# Fit regression model

fit = glm(spam ~ ., data = train, family = binomial())

summary(fit)

# Call:

# glm(formula = spam ~ ., family = binomial(), data = train)

#

# Deviance Residuals:

# Min 1Q Median 3Q Max

# -4.5172 -0.2039 0.0000 0.1111 5.4944

# Coefficients:

# Estimate Std. Error z value Pr(>|z|)

# (Intercept) -1.511e+00 1.546e-01 -9.772 < 2e-16 ***

# A.1 -4.546e-01 2.560e-01 -1.776 0.075720 .

# A.2 -1.630e-01 7.731e-02 -2.108 0.035043 *

# A.3 1.487e-01 1.261e-01 1.179 0.238591

# A.4 2.055e+00 1.467e+00 1.401 0.161153

# A.5 6.165e-01 1.191e-01 5.177 2.25e-07 ***

# A.6 7.156e-01 2.768e-01 2.585 0.009747 **

# A.7 2.606e+00 3.917e-01 6.652 2.88e-11 ***

# A.8 6.750e-01 2.284e-01 2.955 0.003127 **

# A.9 1.197e+00 3.362e-01 3.559 0.000373 ***

# Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 . 0.1 1

### Make predictions

preds = predict(fit, test, type = ’response’)

preds = ifelse(preds > 0.5, 1, 0)

tbl = table(target = test$spam, preds)

tbl

# preds

# target 0 1

# email 535 23

# spam 46 316

sum(diag(tbl)) / sum(tbl)

# 0.925

Big Data Analytics – Análisis de series temporales

La serie temporal es una secuencia de observaciones de variables categóricas o numéricas indexadas por una fecha o marca de tiempo. Un claro ejemplo de datos de series temporales es la serie temporal del precio de una acción. En la siguiente tabla, podemos ver la estructura básica de los datos de series temporales. En este caso las observaciones se registran cada hora.

Normalmente, el primer paso en el análisis de series de tiempo es trazar la serie, esto normalmente se hace con un gráfico de líneas.

La aplicación más común del análisis de series temporales es pronosticar valores futuros de un valor numérico utilizando la estructura temporal de los datos. Esto significa que las observaciones disponibles se utilizan para predecir valores del futuro.

El ordenamiento temporal de los datos implica que los métodos de regresión tradicionales no son útiles. Para construir un pronóstico sólido, necesitamos modelos que tengan en cuenta el orden temporal de los datos.

El modelo más utilizado para el análisis de series temporales se denomina media móvil autorregresiva (ARMA). El modelo consta de dos partes, una parte autorregresiva (AR) y una parte de media móvil (MA). El modelo generalmente se denomina modelo ARMA (p, q) , donde p es el orden de la parte autorregresiva y q es el orden de la parte de promedio móvil.

Modelo autorregresivo

El AR(p) se lee como un modelo autorregresivo de orden p. Matemáticamente se escribe como −

Xt= c +∑yo = 1PAGϕiXt – yo+εt��=�+∑�=1�����−�+��

donde {φ ₁ , …, φ _p } son parámetros a estimar, c es una constante y la variable aleatoria ε _t representa el ruido blanco. Algunas restricciones son necesarias en los valores de los parámetros para que el modelo permanezca estacionario.

Media móvil

La notación MA(q) se refiere al modelo de promedio móvil de orden q −

Xt= m +εt+∑yo = 1qθiεt – yo��=�+��+∑�=1�����−�

donde θ ₁ , …, θ _q son los parámetros del modelo, μ es la expectativa de X _t , y ε _t , ε _{t − 1} , … son términos de error de ruido blanco.

Media móvil autorregresiva

El modelo ARMA(p, q) combina p términos autorregresivos y q términos de promedio móvil. Matemáticamente el modelo se expresa con la siguiente fórmula −

Xt= c +εt+∑yo = 1PAGϕiXt – 1+∑yo = 1qθiεt – yo��=�+��+∑�=1�����−1+∑�=1�����−�

Podemos ver que el modelo ARMA(p, q) es una combinación de los modelos AR(p) y MA(q) .

Para dar una idea del modelo, considere que la parte AR de la ecuación busca estimar parámetros para X _{t − i} observaciones de para predecir el valor de la variable en X _t . Es al final un promedio ponderado de los valores pasados. La sección MA usa el mismo enfoque pero con el error de las observaciones anteriores, ε _{t − i} . Entonces, al final, el resultado del modelo es un promedio ponderado.

El siguiente fragmento de código demuestra cómo implementar un ARMA(p, q) en R .

# install.packages(“forecast”)

library(“forecast”)

# Read the data

data = scan(‘fancy.dat’)

ts_data <- ts(data, frequency = 12, start = c(1987,1))

ts_data

plot.ts(ts_data)

Trazar los datos es normalmente el primer paso para averiguar si hay una estructura temporal en los datos. Podemos ver en la gráfica que hay fuertes picos al final de cada año.

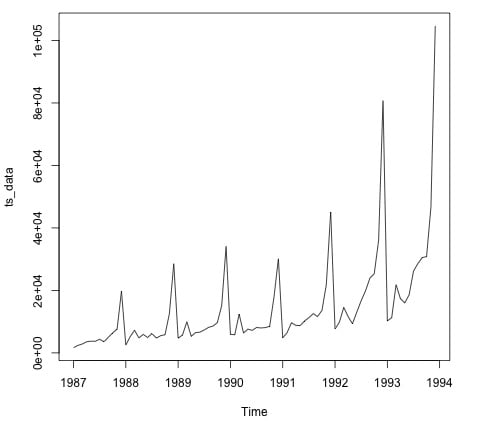
El siguiente código ajusta un modelo ARMA a los datos. Ejecuta varias combinaciones de modelos y selecciona el que tiene menos error.

# Fit the ARMA model

fit = auto.arima(ts_data)

summary(fit)

# Series: ts_data

# ARIMA(1,1,1)(0,1,1)[12]

# Coefficients:

# ar1 ma1 sma1

# 0.2401 -0.9013 0.7499

# s.e. 0.1427 0.0709 0.1790

#

# sigma^2 estimated as 15464184: log likelihood = -693.69

# AIC = 1395.38 AICc = 1395.98 BIC = 1404.43

# Training set error measures:

# ME RMSE MAE MPE MAPE MASE ACF1

# Training set 328.301 3615.374 2171.002 -2.481166 15.97302 0.4905797 -0.02521172

Análisis de Big Data – Análisis de texto

En este capítulo, usaremos los datos recopilados en la parte 1 del libro. Los datos tienen texto que describe los perfiles de los trabajadores independientes y la tarifa por hora que cobran en USD. La idea de la siguiente sección es ajustar un modelo que, dadas las habilidades de un trabajador independiente, podamos predecir su salario por hora.

El siguiente código muestra cómo convertir el texto sin procesar que en este caso tiene las habilidades de un usuario en una matriz de bolsa de palabras. Para ello utilizamos una librería de R llamada tm. Esto significa que para cada palabra del corpus creamos una variable con la cantidad de ocurrencias de cada variable.

library(tm)

library(data.table)

source(‘text_analytics/text_analytics_functions.R’)

data = fread(‘text_analytics/data/profiles.txt’)

rate = as.numeric(data$rate)

keep = !is.na(rate)

rate = rate[keep]

### Make bag of words of title and body

X_all = bag_words(data$user_skills[keep])

X_all = removeSparseTerms(X_all, 0.999)

X_all

# <<DocumentTermMatrix (documents: 389, terms: 1422)>>

# Non-/sparse entries: 4057/549101

# Sparsity : 99%

# Maximal term length: 80

# Weighting : term frequency – inverse document frequency (normalized) (tf-idf)

### Make a sparse matrix with all the data

X_all <- as_sparseMatrix(X_all)

Ahora que tenemos el texto representado como una matriz dispersa, podemos ajustar un modelo que dará una solución dispersa. Una buena alternativa para este caso es usar LASSO (operador de selección y contracción mínima absoluta). Este es un modelo de regresión que puede seleccionar las características más relevantes para predecir el objetivo.

train_inx = 1:200

X_train = X_all[train_inx, ]

y_train = rate[train_inx]

X_test = X_all[-train_inx, ]

y_test = rate[-train_inx]

# Train a regression model

library(glmnet)

fit <- cv.glmnet(x = X_train, y = y_train,

family = ‘gaussian’, alpha = 1,

nfolds = 3, type.measure = ‘mae’)

plot(fit)

# Make predictions

predictions = predict(fit, newx = X_test)

predictions = as.vector(predictions[,1])

head(predictions)

# 36.23598 36.43046 51.69786 26.06811 35.13185 37.66367

# We can compute the mean absolute error for the test data

mean(abs(y_test – predictions))

# 15.02175

Ahora tenemos un modelo que dado un conjunto de habilidades es capaz de predecir el salario por hora de un freelancer. Si se recopilan más datos, el rendimiento del modelo mejorará, pero el código para implementar esta canalización sería el mismo.

Big Data Analytics – Aprendizaje en línea

El aprendizaje en línea es un subcampo del aprendizaje automático que permite escalar modelos de aprendizaje supervisado a conjuntos de datos masivos. La idea básica es que no necesitamos leer todos los datos en la memoria para ajustar un modelo, solo necesitamos leer cada instancia a la vez.

En este caso, mostraremos cómo implementar un algoritmo de aprendizaje en línea usando regresión logística. Como en la mayoría de los algoritmos de aprendizaje supervisado, existe una función de coste que se minimiza. En la regresión logística, la función de costo se define como −

j( θ )=− 1metro[∑yo = 1metroy( yo )registro _ _(hθ(X( yo )) ) + ( 1 −y( yo )) registro _ _( 1 −hθ(X( yo )) ) ]�(�)=−1�[∑�=1��(�)���(ℎ�(�(�)))+(1−�(�))���(1−ℎ�(�(�)))]

donde J(θ) representa la función de costo y h _θ (x) representa la hipótesis. En el caso de la regresión logística se define con la siguiente fórmula −

hθ( X ) =11 +miθTXℎ�(�)=11+����

Ahora que hemos definido la función de costo, necesitamos encontrar un algoritmo para minimizarla. El algoritmo más simple para lograr esto se llama descenso de gradiente estocástico. La regla de actualización del algoritmo para los pesos del modelo de regresión logística se define como −

θj: =θj− α (hθ( x ) − y) x��:=��−�(ℎ�(�)−�)�

Hay varias implementaciones del siguiente algoritmo, pero la implementada en la biblioteca de vocales wabbit es, con mucho, la más desarrollada. La biblioteca permite el entrenamiento de modelos de regresión a gran escala y utiliza pequeñas cantidades de RAM. En las propias palabras de los creadores, se describe como: “El proyecto Vowpal Wabbit (VW) es un sistema de aprendizaje rápido fuera del núcleo patrocinado por Microsoft Research y (anteriormente) Yahoo! Research”.

Trabajaremos con el conjunto de datos titánico de una competencia de kaggle . Los datos originales se pueden encontrar en la carpeta bda/part3/vw . Aquí, tenemos dos archivos:

• Tenemos datos de entrenamiento (train_titanic.csv), y
• datos sin etiquetar para hacer nuevas predicciones (test_titanic.csv).

Para convertir el formato csv al formato de entrada de vocales wabbit , use el script python csv_to_vowpal_wabbit.py . Obviamente necesitarás tener Python instalado para esto. Navegue a la carpeta bda/part3/vw , abra la terminal y ejecute el siguiente comando:

python csv_to_vowpal_wabbit.py

Tenga en cuenta que para esta sección, si está utilizando Windows, deberá instalar una línea de comando de Unix, ingrese al sitio web de cygwin para eso.

Abra la terminal y también en la carpeta bda/part3/vw y ejecute el siguiente comando:

vw train_titanic.vw -f model.vw –binary –passes 20 -c -q ff –sgd –l1

0.00000001 –l2 0.0000001 –learning_rate 0.5 –loss_function logistic

Analicemos qué significa cada argumento de la llamada vw .

• -f model.vw − significa que estamos guardando el modelo en el archivo model.vw para hacer predicciones más adelante
• –binary : informa la pérdida como clasificación binaria con etiquetas -1,1
• –pasa 20 − Los datos se usan 20 veces para aprender los pesos
• -c − crea un archivo de caché
• -q ff – Usar características cuadráticas en el espacio de nombres f
• –sgd : use la actualización de descenso de gradiente estocástico regular/clásico/simple, es decir, no adaptativo, no normalizado y no invariante.
• –l1 –l2 − Regularización de normas L1 y L2
• –learning_rate 0.5 − La tasa de aprendizaje α tal como se define en la fórmula de la regla de actualización

El siguiente código muestra los resultados de ejecutar el modelo de regresión en la línea de comando. En los resultados, obtenemos la pérdida de registro promedio y un pequeño informe del rendimiento del algoritmo.

-loss_function logistic

creating quadratic features for pairs: ff

using l1 regularization = 1e-08

using l2 regularization = 1e-07

final_regressor = model.vw

Num weight bits = 18

learning rate = 0.5

initial_t = 1

power_t = 0.5

decay_learning_rate = 1

using cache_file = train_titanic.vw.cache

ignoring text input in favor of cache input

num sources = 1

average since example example current current current

loss last counter weight label predict features

0.000000 0.000000 1 1.0 -1.0000 -1.0000 57

0.500000 1.000000 2 2.0 1.0000 -1.0000 57

0.250000 0.000000 4 4.0 1.0000 1.0000 57

0.375000 0.500000 8 8.0 -1.0000 -1.0000 73

0.625000 0.875000 16 16.0 -1.0000 1.0000 73

0.468750 0.312500 32 32.0 -1.0000 -1.0000 57

0.468750 0.468750 64 64.0 -1.0000 1.0000 43

0.375000 0.281250 128 128.0 1.0000 -1.0000 43

0.351562 0.328125 256 256.0 1.0000 -1.0000 43

0.359375 0.367188 512 512.0 -1.0000 1.0000 57

0.274336 0.274336 1024 1024.0 -1.0000 -1.0000 57 h

0.281938 0.289474 2048 2048.0 -1.0000 -1.0000 43 h

0.246696 0.211454 4096 4096.0 -1.0000 -1.0000 43 h

0.218922 0.191209 8192 8192.0 1.0000 1.0000 43 h

finished run

number of examples per pass = 802

passes used = 11

weighted example sum = 8822

weighted label sum = -2288

average loss = 0.179775 h

best constant = -0.530826

best constant’s loss = 0.659128

total feature number = 427878

Ahora podemos usar el modelo.vw que entrenamos para generar predicciones con nuevos datos.

vw -d test_titanic.vw -t -i model.vw -p predictions.txt

Las predicciones generadas en el comando anterior no están normalizadas para ajustarse al rango [0, 1]. Para hacer esto, usamos una transformación sigmoidea.

# Read the predictions

preds = fread(‘vw/predictions.txt’)

# Define the sigmoid function

sigmoid = function(x) {

1 / (1 + exp(-x))

}

probs = sigmoid(preds[[1]])

# Generate class labels

preds = ifelse(probs > 0.5, 1, 0)

head(preds)

# [1] 0 1 0 0 1 0