🕑 Tiempo de lectura: 1 minuto
Las vigas tienen varias características que los ingenieros deben conocer porque determinan cómo se comporta la viga bajo carga y, en última instancia, representan áreas potenciales o mecanismos de falla. Los principales son:
- Momento de inercia de área (también conocido como segundo momento de inercia): Esta es una medida de la resistencia geométrica de la viga a la flexión, dependiendo del perfil de la sección transversal de la viga.
- Momento de flexión: generalmente se muestra en un diagrama de momento de flexión, a menudo relacionado con la desviación de la viga, y se puede usar para calcular el área donde la fuerza de flexión es mayor y, por lo tanto, es más probable que ceda. También indica qué sección de la viga está comprimida o traccionada.
- Deflexión del haz: La deflexión del haz tiende a ser indeseable y se correlaciona con el momento de flexión.
- Diagramas de corte: se utilizan para mostrar las concentraciones de tensión a lo largo de las vigas y proporcionan un medio para identificar áreas de fuerza de corte máxima donde es probable que las vigas fallen debido al corte.
>momento de inercia del área
El momento de inercia del área (I) es una propiedad de la geometría utilizada para predecir la resistencia a la flexión y deflexión de las vigas. Se calcula a partir del área de la sección transversal física de la viga y relaciona la masa del perfil con el eje neutro (el área donde la viga no está ni en compresión ni en tracción, como se muestra en la Figura 5). Carga: La mayoría de las vigas, excepto las secciones circulares y de caja sólida y hueca, tienen diferentes momentos geométricos de inercia cuando se cargan desde la dirección horizontal o vertical.
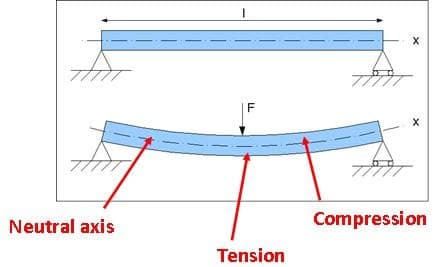
Figura 5 – a) Una viga simplemente apoyada de longitud l sin aplicación de fuerza. b) Una viga simplemente apoyada con una carga puntual central (fuerza) F que causa flexión. El momento de inercia del área se puede calcular a partir de los primeros principios para cualquier perfil de sección transversal utilizando la siguiente fórmula:
![]()
Sin embargo, para perfiles generales de vigas, se utilizan fórmulas estándar.
Viga en I/haz universal
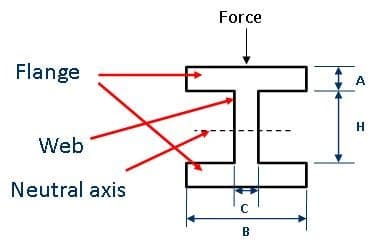
Figura 6: perfil de la sección transversal de una viga en I cargada paralela al alma. Las vigas en I o vigas universales tienen el perfil de sección transversal más eficiente y ofrecen un alto momento de área porque la mayor parte de su material está ubicado lejos del eje neutral. Se puede calcular usando la siguiente fórmula:
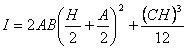
Como se muestra en la Figura 6, esto solo es adecuado para cargar en paralelo a la red, ya que la carga perpendicular a la red es menos eficiente.
parte de la caja
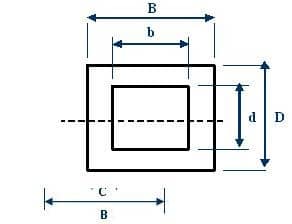
Figura 7 – Perfil de sección transversal de sección de caja
La sección de caja tiene un perfil que permite la carga más eficiente tanto horizontal como verticalmente. Debido al bajo valor del momento de inercia del área, la rigidez es baja. Se puede calcular usando la siguiente fórmula:
![]()
Ilustración de momento flector y cortante
Los diagramas de momento de flexión y cortante generalmente se dibujan junto con los diagramas de perfil de viga como se muestra a continuación. Esto permite una representación precisa del comportamiento del haz.
a) representa una viga sujeta a una carga uniformemente distribuida (udl) de magnitud w sobre una longitud l. La fuerza total sobre la viga es wl. La viga está simplemente apoyada con una fuerza de reacción R. La distancia x representa un punto arbitrario a lo largo de la viga.
b) El diagrama de fuerza de corte muestra el área de corte máximo. Para este haz, estos están correlacionados con las fuerzas de reacción. La pendiente del diagrama de fuerza cortante es igual a la magnitud de la carga distribuida. Una fuerza cortante positiva gira la viga en sentido horario y una fuerza cortante negativa gira la viga en sentido antihorario.
C) El momento de flexión máximo ocurre cuando no hay fuerza cortante en la viga. Dado que las vigas están simplemente apoyadas y están sujetas solo a fuerzas de reacción verticales, no se producen momentos de flexión en estos puntos. Si la viga está restringida como en una situación de voladizo, pueden ocurrir momentos de flexión en cualquiera de los extremos. En relación con el diagrama de carga de la viga, el valor máximo de la fuerza cortante y el momento de flexión y el valor a la distancia x a lo largo de la viga se pueden calcular utilizando las siguientes fórmulas::
fuerza de reacción y fuerza de corte máxima y fuerza de corte a la distancia x
![]()
Momento flector máximo y momento flector a la distancia x
![]()
deflexión máxima y deflexión a la distancia x
![]()
Estas fórmulas son específicas para esta situación de haz. Esta es una carga uniformemente distribuida con soportes simples como se muestra. Para vigas en voladizo o soportes con diversos grados de libertad (que se refiere a restricciones horizontales que someten la viga a momentos de rotación en esta posición), se requiere una fórmula diferente. Todas las ecuaciones se pueden calcular a partir de los primeros principios, pero para mayor comodidad, está disponible la tabla de búsqueda contenida en Roark’s Stress and Strain Equations. Se muestra que las fórmulas para la desviación máxima del haz y la desviación a la distancia x dependen del módulo de Young E y el momento de inercia I. Aquí, las fuerzas cortantes y los momentos flectores son independientes de estas propiedades de la viga.
