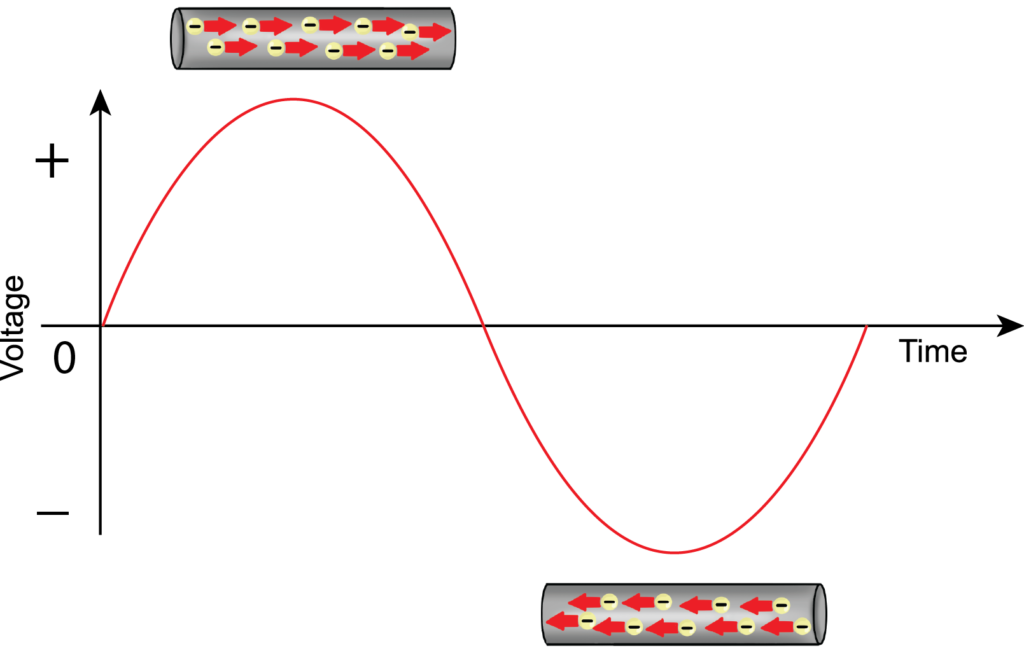
Los circuitos de corriente alterna o CA son simplemente circuitos alimentados por una fuente alterna, ya sea de corriente o de tensión. Una tensión o corriente alterna es aquella en la que la cantidad de la tensión o de la corriente se altera en torno a un valor medio distinto y se invierte el sentido periódicamente.
En un circuito de corriente alterna, la tensión y la corriente de la fuente tienen un ángulo de fase, que puede calcularse dividiendo la resistencia por la impedancia. El ángulo de fase influye en la potencia media suministrada a un circuito RLC.
En el sitio web de Linquip hay una lista completa de servicios de dispositivos de CA que cubre todas las flotas de OEM. Los proveedores de Linquip pueden ayudarle con esto. Llame a los expertos en dispositivos de CA de Linquip para obtener más información sobre cómo conectar con un grupo diverso de proveedores de servicios que ofrecen constantemente productos de alta calidad.
La mayoría de los sistemas y aparatos domésticos e industriales de hoy en día se alimentan con corriente alterna.
Todos los dispositivos enchufados a la corriente continua basados en baterías recargables funcionan técnicamente en base a una corriente alterna. Todos los dispositivos de CC utilizan la energía de CC obtenida de la CA para cargar su sistema de alimentación y sus baterías.
El circuito de corriente alterna se creó por primera vez en la década de 1980, cuando Tesla pretendía resolver las numerosas incapacidades de los generadores de CC de Thomas Edison. Intentó presentar una forma de transferir electricidad a un alto voltaje.
Luego, empleando transformadores para subirla o bajarla para su distribución, se conseguiría minimizar la pérdida de energía a través de largas distancias, que era el centro de los problemas de la corriente continua en aquel momento.
Tabla de contenido
Corriente continua frente a corriente alterna (CA frente a CC)
La CA y la CC difieren en muchos aspectos, desde la transmisión hasta la generación y distribución. La diferencia significativa entre la CC y la CA, que es también la base de sus diversas características, es la dirección del flujo de electricidad.
En la CC, los electrones fluyen continuamente en una dirección específica o hacia adelante, pero en el sistema de CA, los electrones intercambian su dirección de movimiento en intervalos periódicos. Esta corriente alterna también provoca la alternancia del valor de la tensión, ya que cambia de negativo a positivo en función de la corriente.
¿Qué es un circuito de corriente alterna?
Los circuitos eléctricos y electrónicos incluyen muchos componentes de conexión diferentes para formar un circuito cerrado y completo. Los principales componentes pasivos empleados en cualquier circuito son el condensador, la resistencia y el inductor. Los tres componentes pasivos nombrados tienen una característica en común: limitan la corriente eléctrica en un circuito, pero de forma totalmente distinta.
La corriente eléctrica puede pasar por un circuito de dos maneras. Si pasa en una sola dirección, se denomina corriente continua (DC). Si la corriente eléctrica alterna en varias direcciones de ida y vuelta, se denomina Corriente Alterna (CA). Al ofrecer una impedancia dentro de un circuito, los componentes pasivos de los circuitos de CA actúan de forma muy diferente a los de los circuitos de CC.
Los componentes pasivos del circuito consumen energía eléctrica. Por lo tanto, no pueden amplificar o aumentar la potencia de cualquier señal eléctrica que se les aplique. Sencillamente, todo se debe a que son pasivos y siempre tendrán una ganancia menor. Los componentes pasivos colocados en un circuito eléctrico y electrónico pueden combinarse en un número infinito de diseños, como se muestra a continuación, y el rendimiento de estos circuitos se basa en la interacción entre sus diversas propiedades eléctricas.
¿Cómo se analiza un circuito eléctrico?
La Ley de Ohm es la ley más importante en el análisis de circuitos. Tensión=Resistencia*Corriente (V=IR) indica que la tensión a través de un elemento es igual a la corriente del elemento por la corriente que fluye a través del elemento. La cantidad de potencial eléctrico medida en voltios se denomina tensión (V).
¿Qué son el reactivo y la impedancia?
El tipo de circuitos en los que la corriente es proporcional a la tensión se denominan circuitos lineales. En una resistencia, la relación entre la tensión y la corriente es su resistencia. La resistencia no tiene la independencia a la frecuencia, y tienen dos fases. Aún así, los circuitos con sólo resistencias no son muy excitantes y aplicables.
Por lo general, la frecuencia no afecta a la relación entre la tensión y la corriente, y hay una diferencia de fase. Por eso, el nombre general de la relación entre la tensión y la corriente es impedancia. El símbolo de la impedancia es Z. La resistencia es un caso particular de impedancia. Otro ejemplo especial es que la corriente y la tensión estén desfasadas en 90°; este es un caso esencial porque no hay pérdida de potencia en el circuito cuando esto ocurre. En este caso, en el que la corriente y la tensión están desfasadas 90°, denominamos reactancia a la relación entre la tensión y la corriente, y su símbolo es X.
Terminología
Para la compresión, indicaremos la diferencia de potencial eléctrico como tensión. Consideraremos las tensiones y las corrientes como una función que varía sinusoidalmente con el tiempo y utilizaremos las minúsculas i y v para la corriente y la tensión cuando analicemos explícitamente su variación. Representaremos la amplitud o valor máximo de la variación sinusoidal por Vm e Im, mientras que V = Vm/√2 e I = Im/√2 sin subíndices se refieren a sus valores eficaces. Para entender el origen de las tensiones de variación sinusoidal y cómo las utilizamos, consulta este post.
La tensión y la corriente que utilizamos en CA pueden presentarse como las siguientes ecuaciones:
v = v
i = i
donde:
\omega = 2πf = la frecuencia angular
f = la frecuencia ordinaria o cíclica = el número de oscilaciones completas por segundo.
\varphi = la diferencia de fase entre la tensión y la corriente.
Componentes pasivos en circuitos de CA
Podemos denominar R como resistencia, C como capacitancia y L como inductancia. Tanto si utilizamos resistencias en circuitos de CC como de CA, siempre tienen el mismo valor de resistencia en el sistema, independientemente de la frecuencia de alimentación. Todo se debe a que las resistencias se identifican como puras, teniendo características parásitas como inductancia cero L = 0 y capacitancia infinita C = ∞. Además, para un circuito totalmente resistivo, siempre tenemos una tensión y una corriente en fase, por lo que podemos encontrar la potencia consumida en cualquier instante multiplicando la tensión por la corriente.
Por otro lado, los condensadores y los inductores tienen un tipo distinto de resistencia a la corriente alterna conocido como reactancia, como ya se ha mencionado (XL y XC). La reactancia también bloquea el flujo de corriente, pero el valor de la reactancia no es una cantidad fija para un condensador o un inductor en comparación con una resistencia con un valor fijo de resistencia. La cantidad de reactancia para un inductor o un condensador se basa en la frecuencia de la corriente de alimentación y el valor de CC del propio elemento.
Además, existe una lista de componentes pasivos de uso común en los circuitos de CA y sus correspondientes ecuaciones que pueden aplicarse para encontrar su impedancia y el valor de la reactancia de la corriente del circuito. Hay que mencionar que aquí presentamos un inductor o condensador teóricamente perfecto (puro) que no tiene ninguna resistencia. Pero en el mundo real, siempre tenemos una combinación de los componentes mencionados anteriormente, que incluye también la resistencia.
Circuito totalmente resistivo
Las resistencias impiden, regulan o fijan el flujo de la corriente en un camino distinto o imponen un corte de tensión en un circuito eléctrico en base a este flujo de corriente. Las resistencias tienen una especie de impedancia llamada resistencia ( R ). La cantidad resistiva de una resistencia se mide en Ohms, Ω, y puede encontrarse tanto en un valor fijo como en un valor cambiante (potenciómetros).
La impedancia y el valor de la corriente se pueden encontrar utilizando las siguientes ecuaciones:
Z=\frac{V_R}{I_R}=R
Z=\angle 0^{\circ} = R+J0
I_S=\frac{V_S}{R}
Circuito totalmente capacitivo
El condensador es un componente que tiene la capacidad y puede guardar energía en forma de carga eléctrica, igual que una pequeña batería. La cantidad de capacidad de un condensador se mide en Faradios (F), y en el circuito de corriente continua, un condensador tiene una impedancia infinita (circuito abierto). En cambio, un condensador tiene una impedancia nula (cortocircuito) a frecuencias muy altas. La impedancia y el valor de la corriente se pueden encontrar utilizando las siguientes ecuaciones:
X_C =\frac{V_C}{I_C}=\frac{1}{2\pi fC}
Z=\angle -90^{\circ}=0-jX_C
I_S= \frac{V_S}{X_S}
Circuito totalmente inductivo
Un inductor incluye una bobina de alambre que induce un campo magnético en su interior o en un núcleo central debido a la corriente que circula por la bobina. La cantidad de inductancia de un inductor se mide en la unidad Henries (H). En circuitos de corriente continua, un inductor es un cortocircuito y tiene una impedancia nula. En cambio, a altas frecuencias, un inductor tiene una impedancia infinita (circuito abierto). La impedancia y el valor de la corriente se pueden encontrar utilizando las siguientes ecuaciones:
X_L =\frac{V_L}{I_L}=2\pi fL
Z=\angle 90^{\circ}=0+jX_C
I_S= \frac{V_S}{X_L}
Circuitos de CA en serie
Podemos conectar componentes pasivos en combinaciones en serie en circuitos de CA para formar circuitos RC, RL y LC, como se explica a continuación.
Circuito RC en serie
El circuito y la ecuación del circuito RC en serie son:
Z= \sqrt{R^{2}+X_C^{2}}
Z=\angle -\phi = R-jX_C
\phi (90\rightarrow 0) = tan^{-1}(-\frac{X_C}{R})
I_S= \frac{V_S}{\sqrt{R^{2}+X_C^{2}}}
V_S=\sqrt{V_R^{2}+V_C^{2}}
Circuito RL en serie
El diagrama del circuito y la ecuación del circuito RL en serie son:
Z= \sqrt{R^{2}+X_L^{2}}
Z=\angle \phi = R+jX_C
\phi (90\rightarrow 0) = tan^{-1}(\frac{X_L}{R})
I_S= \frac{V_S}{\sqrt{R^{2}+X_L^{2}}}
V_S=\sqrt{V_R^{2}+V_L^{2}}

Circuito LC en serie
El diagrama del circuito y la ecuación del circuito LC en serie son:
Z=\sqrt{(X_C-X_L)^{2}}
\therefore Z= X_C-X_L or X_L-X_C
Z=\angle (\phi _1+\phi _2)= 0 + jX_L-jX_C
f_r=\frac{1}{2\pi \sqrt{LC}}
I_S=I_L=I_C

Circuitos de CA en paralelo
Podemos conectar componentes pasivos en combinaciones en serie en circuitos de CA para formar circuitos RC, RL y LC, como se explica a continuación.
Circuito RC en paralelo
El diagrama del circuito y la ecuación del circuito RC paralelo son:
I_R=\frac{V_s}{R}, I_C=\frac{V_S}{X_C}
I_S=\sqrt{I_R^{2}+I_C^{2}}
\phi = tan^{-1}(\frac{I_C}{I_R})
Y= \frac{1}{Z}=\sqrt{G^{2}+B_c^{2}}
V_S=V_C=V_R

Circuito RL en paralelo
El diagrama del circuito y la ecuación del circuito RL en paralelo son:
I_L=\frac{V_s}{R}, I_C=\frac{V_S}{X_L}
I_S=\sqrt{I_R^{2}+I_L^{2}}
\phi = tan^{-1}(\frac{I_L}{I_R})
Y= \frac{1}{Z}=\sqrt{G^{2}+B_L^{2}}
V_S=V_L=V_R

Circuito LC en paralelo
El diagrama del circuito y la ecuación del circuito LC en paralelo son:
B_L=\frac{1}{X_L}, B_C=\frac{1}{X_C}
Y=\frac{1}{Z}=B_L+B_C
f_R=\frac{1}{2\pi \sqrt{LC}}
V_S=V_L=V_C

Circuitos RLC
Podemos conectar los tres componentes pasivos en un circuito de CA, tanto en combinaciones RLC en serie como en paralelo, como se explica a continuación.
Circuito RLC en serie
El diagrama del circuito y la ecuación del circuito RLC en serie son:
Z= \sqrt{R^{2}+(X_C-X_l)^{2}}
Z=\angle \phi =R+jX
V_S=\sqrt{V_R^{2}+(V_C-V_L)^{2})}
I_S=\frac{V_s}{Z}=\frac{V_S}{\sqrt{R^{2}+(X_C-X_l)^{2}}}
\phi = tan^{-1}(\frac{X_L-X_C}{R})
I_S=I_R=I_C=I_L

Circuito RLC en paralelo
El diagrama del circuito y la ecuación para el circuito RLC paralelo son:
G=\frac{1}{R}, B_L=\frac{1}{X_L} ,B_C=\frac{1}{X_C}
Y=\frac{1}{Z}=\sqrt{G^{2}+(B_l-B_C)^{2}}
I_S=\sqrt{I_R^{2}+(I_L-I-C)^{2}}
f_R=\frac{1}{2\pi\sqrt{LC}}
V_S=V_C=V_R=V_L

Se ha demostrado anteriormente en los circuitos de CA que los componentes pasivos se comportan de manera muy diferente que cuando se emplean en un circuito de CC debido a la presencia de la frecuencia ( ƒ ). En un circuito totalmente resistivo, tenemos corriente y tensión en fase. En un circuito totalmente capacitivo, la corriente en el condensador tiene -90o con la tensión, mientras que es 90o para un circuito totalmente inductivo.
En los circuitos en serie, la suma fasorial de las tensiones a través de los componentes del circuito es equivalente a la tensión de alimentación (VS). Por otro lado, en un circuito en paralelo, la suma fasorial de las corrientes que circulan por cada elemento es igual a la corriente de alimentación (IS).
Tanto para la conexión en serie como en paralelo de los circuitos RLC, la resonancia se produce en XL = XC cuando la corriente de la fuente está “en fase” con la tensión de alimentación del circuito. La resonancia de un circuito en serie se identifica como un circuito aceptor, y un circuito de resonancia en paralelo se identifica como un circuito rechazador.
Potencia en el circuito de CA
En los circuitos de CC, la potencia de los componentes es simplemente la salida de la tensión de CC multiplicada por la corriente en vatios. Sin embargo, para un circuito de CA con elementos reactivos, tenemos que evaluar la potencia consumida de forma diferente.
La potencia eléctrica es la energía consumida en un circuito. Todos los elementos y dispositivos eléctricos y electrónicos tienen una limitación para la cantidad de energía eléctrica que pueden manejar con seguridad. Por ejemplo, tenemos una resistencia de 1/4 de vatio o un amplificador de 20 vatios.
La cantidad de energía en los circuitos en cualquier momento se llama potencia instantánea y se conoce por la famosa relación de potencia igual a amperios por voltios (P = VI). En consecuencia, un vatio será igual al resultado de un voltio por un amperio (un vatio es la tasa de consumo de energía de un julio por segundo).
Así pues, la potencia consumida o proporcionada por un elemento del circuito es la tensión a través del elemento y la corriente que circula por él. Supongamos que tenemos una resistencia de “R” ohmios en un circuito de corriente continua. En ese caso, la potencia disipada en vatios viene dada por cualquiera de las siguientes ecuaciones generalizadas:
P=V\times I=R\times I^{2}=\frac{V^{2}}{R}
where:
V: DC voltage
I: DC current
R: Resistance value.
La energía eléctrica en un circuito de CA
En los circuitos de CC, las tensiones y las corrientes son constantes y no varían con el tiempo, ya que no existe una función de onda sinusoidal relacionada con la alimentación. Por el contrario, los valores instantáneos de la corriente, la tensión y la potencia resultante en un circuito de CA cambian continuamente por la alimentación. Por lo tanto, no podemos calcular la potencia en los circuitos de CA igual que el método anterior. Sin embargo, podemos seguir asumiendo que la potencia es igual a los amperios (i) por la tensión (v).
Otro punto crítico es que los circuitos de CA tienen reactancia, por lo que los componentes crean campos magnéticos y/o eléctricos. A diferencia de un elemento puramente resistivo, la potencia se deposita y luego se devuelve al circuito al pasar la forma de onda sinusoidal en un ciclo periódico completo.
Como resultado, la potencia media consumida por un circuito es la suma de la energía almacenada y la potencia devuelta en un ciclo completo. El consumo medio de un circuito es la potencia instantánea media durante un ciclo completo. La potencia instantánea (p) puede definirse como la tensión instantánea (v) por la corriente instantánea (i).
Suponiendo las formas de onda sinusoidales de la tensión y la corriente, tenemos:
P=v\times i
V=V_msin(\omega t+\phi _v)
i=I_msin(\omega t+\phi _i)
p= [V_msin(\omega t+\theta _v)\times I_msin(\omega t+\theta _i)]
\therefore V_mI_m(sin(\omega t+\theta _i)\times sin(\omega t+\theta _v) )
El producto trigonométrico a la suma es:
sin(A+B)=\frac{1}{2}[cos(A-B)-cos(A+B)]
Donde \theta =\theta _v-\theta _i , y colocando en la ecuación anterior tenemos
p=\frac{V_mI_m}{2})(cos(\theta )-cos(2\omega t+\theta ))
\frac{V_mI_m}{2}=\frac{V_m}{\sqrt{2}}\times \frac{I_m}{\sqrt{2}}=V_{RMS}\times I_{RMS}
Donde VRMS and IRMS son los valores de la media cuadrática de las formas de onda sinusoidales de v e i, respectivamente. Por lo tanto, podemos mostrar la potencia instantánea como
P=VIcos\theta – cos(2\omega t+\theta ))
Esta ecuación nos muestra que la potencia instantánea de CA incluye dos partes diferentes y es la suma de dos términos. La segunda parte es una función sinusoidal del tiempo con una frecuencia del doble de la frecuencia angular de la alimentación. Sin embargo, el primer término es una constante cuyo valor se basa en la diferencia de fase, θ, entre la tensión y la corriente.
Como la potencia instantánea varía continuamente con la función sinusoidal en el tiempo, es difícil de medir. Por lo tanto, es más conveniente y sencillo emplear el valor medio o la media de la potencia. Así, el valor medio de la potencia instantánea viene dado simplemente por la siguiente ecuación a lo largo de un determinado número de ciclos:
p=V\times I\times cos(\theta )
La potencia de CA consumida en un circuito también se puede calcular utilizando la impedancia (Z) del circuito como se presenta a continuación:
Z=\sqrt{R^{2}+(X_L-X_C)^{2}}
\theta =cos^{-1}\frac{R}{Z}=sin^{-1}\frac{X_L}{Z}=tan^{-1}\frac{X_L}{R}
\therefore p=\frac{V^{2}}{Z}cos\theta =I^{2}Zcos\theta